3.2: Entropy

\( \begin{aligned} d E &=T d S-p d V+\mu d N \\ &=d Q+d W_{\mathrm{conf}}+d W_{\mathrm{diss}} \\ & \geq d Q+d W_{\mathrm{conf}} \end{aligned}.\)

but

\( d W_{\mathrm{conf}}=-p d V+\mu d N\)

so

\( T d S>d Q\)

where the equality holds for quasistatic changes.

The operational definition of entropy is that, for a quasistatic change,

\[d S=\frac{d Q}{T}. \label{3.3}\]

If we walk into a laboratory with this definition of entropy, the experimentalist will say “Sure I can find this quantity. I’ve got thermometers; and I’ve got resistors, ammeters, and voltmeters, plus a procedure for using them to calculate heat flow.”

For any change (perhaps quasistatic, perhaps not)

\[d S \geq \frac{d Q}{T}.\]

(The entropy change might be due to heat, might be due to dissipative work, might be due to a combination of the two.)

Configurational entropy vs. thermal entropy

The operational, thermodynamic definition for entropy, Equation \ref{3.3}, was in fact discovered before the more fundamental, conceptual, statistical definition (2.7) was. Because of this dual definition some people get the misconception that there are two kinds of entropy: the statistical kind (“configurational entropy”) and the operational kind (“thermal entropy”). That’s false. These are two different ways of looking at the same thing.

3.2 (I) Ideal gas with variables S and V.

a. Use equation (2.32) to show that for a sample of monatomic ideal gas with a fixed number of particles, the energy function is

\[E(S, V)=E_{0}\left(\frac{V_{0}}{V}\right)^{2 / 3} e^{S / S_{0}},\]

where E₀, V₀, and S₀ are constants with the dimensions of energy, volume, and entropy.

b. Use the formulas

\[ T(S, V)=\frac{\partial E(S, V)}{\partial S} \quad \text { and } \quad p(S, V)=-\frac{\partial E(S, V)}{\partial V}\]

to find the temperature and pressure functions for this sample.

3.3 (I) Dependence of heat and work on path

Suppose the ideal gas sample mentioned in the previous problem undergoes a change from an initial state with volume V₀ and entropy S₀ to a final state with volume 8V₀ and entropy (1+ 5 ln 2)S₀. There are an infinite number of quasistatic paths that execute this change. For example:

A First increase the entropy from S = S₀ to S = (1 + 5 ln 2)S₀, keeping the volume fixed at V = V₀, then expand from V = V₀ to V = 8V₀, keeping the entropy fixed at S = (1 + 5 ln 2)S₀.

B Increase the volume and entropy simultaneously along the path

\[ S(V)=S_{0}\left[\frac{5}{3} \ln \left(\frac{V}{V_{0}}\right)+1\right].\]

C First expand from V = V₀ to V = 8V₀, keeping the entropy fixed at S = S₀, then increase the entropy from S = S₀ to S = (1 + 5 ln 2)S₀, keeping the volume fixed at V = 8V₀.

Each path has the same change in volume, entropy, and energy, but each will have a different heat and work. (Remember that each path is quasistatic.)

a. Calculate the heat absorbed by the sample and the work done on the sample for each of these three paths.

b. Find the difference Q + W for each of these three paths.

c. A fourth path from the initial to the final state involves a non-quasistatic change and the absorption of heat Q = 3E₀. What work is done on the sample during this change?

(In making up this problem I choose somewhat peculiar initial and final states, and connecting paths, so that the above quantities could be calculated analytically. Despite these peculiarities the principle illustrated by the problem should be clear: heat and work depend upon path, but their difference the energy change does not.)

3.4 (I*) Work in terms of p and V

We have so far considered work and heat in a fluid system specified by the variables S, V, and N, and have often assumed that N is constant. Another way of specifying such a system is through the variables p (pressure) and V. This problem considers quasistatic processes described as paths in the (p, V) plane.

a. Show that the work done on the system in changing quasistatically from the initial state (V_i, p_i) to the final state (V_f, p_f) along the path shown in the figure below is the negative of the area under the curve. What is the work done if the path is traversed in the opposite direction?

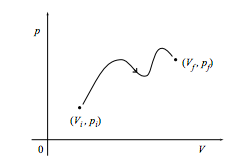
b. What is the work done on the system through the same change along the path below?

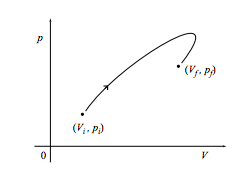
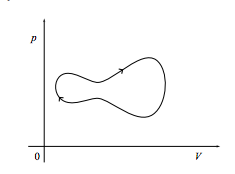
c. Finally, what is the work done on the system if it comes back to its starting point as in the cycle shown below? What if the cycle is instead executed in a counterclockwise fashion?

3.5 (I) Fluid work

In a quasistatic, adiabatic process, a sample of gas expands from V_i = 1 m³ to V_f = 8 m³, while the pressure drops from p_i = 32 Pa to p_f = 1 Pa. It is observed that during this process the pressure and volume are related by

\[p V^{\gamma}=\text { constant },\]

where the constant γ is \( \frac{5}{3}\). Of course, this is not the only process leading from this particular initial state to that particular final state. Find the total work done on the system and heat absorbed by the system in each of the following quasistatic processes, all of which connect the same two thermodynamic states.

a. The adiabatic process described above.

b. At constant pressure, the gas expands from V_i to V_f. (Heat must be added to the system during this expansion in order to keep the pressure constant.) Then at constant volume, the the pressure is reduced from p_i to p_f. (Heat must be extracted from the system during this stage of the process.)

c. The volume is increased and heat is supplied at just the right rate to make the pressure decrease linearly with volume.

d. As in part (b.) but with the two steps performed in opposite order.