11.4: Rotation about an axis versus rotation about a point .

When defining angular quantities (torque, angular acceleration, etc.), it is important to identify whether these are defined relative to an axis or to a point of rotation. This, in turn, determines the vector \(\vec r\) that is involved in the definition of the angular quantities.

Consider a disk of radius \(r\) with a force, \(\vec F\) exerted on its perimeter, as illustrated in Figure \(\PageIndex{1}\). The disk can only rotate about an axis that is perpendicular to the disk and that goes through the center of the disk, like a wheel mounted on an axle. The force has a component, \(\vec F_{plane}\), that lies in the plane perpendicular to the axis of rotation, and a component, \(\vec F_{axis}\), that is parallel to axis of rotation.

Figure \(\PageIndex{1}\): A force exerted on disk that can only rotate about an axis through its center and perpendicular to its plane. Only the component of \(\vec F\) that is in the plane perpendicular to the axis of rotation, \(\vec F\) plane, will contribute to the torque about the axis of rotation.

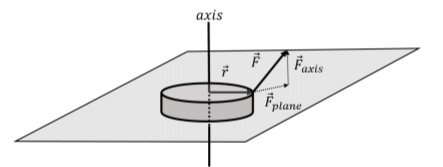
The vector \(\vec r\) is always defined to be perpendicular to the axis of rotation and to go from the axis of rotation to the point where the force \(\vec F\) is exerted, as illustrated. The torque obtained by taking the cross product:

\[\begin{aligned} \vec \tau = \vec r \times \vec F\end{aligned}\]

will be perpendicular to both \(\vec r\) and \(\vec F\), and will thus not be parallel to the axis of rotation. Only the component of the torque that is parallel to the axis of rotation will contribute to rotating the disk about the axis. Only the component of the force that lies in the plane perpendicular to the axis of rotation, \(\vec F_{plane}\), will contribute to the component of the torque about that axis of rotation. Thus, when we need to determine the torque about an axis of rotation, we can consider vectors \(\vec r\) and \(\vec F\) that lie in the plane perpendicular to the axis of rotation. The torque of \(\vec F\) relative to the axis of rotation is thus:

\[\begin{aligned} \vec \tau_{axis} = \vec r \times \vec F_{plane}\end{aligned}\]

Furthermore, only the component of \(\vec F_{plane}\) that is perpendicular to \(\vec r\) will contribute to that torque, as we saw in the previous section.

In general, solid objects such as a disk can only rotate about an axis. In that case, one can consider only the components of forces that lie in the plane perpendicular to the axis of rotation in order to calculate the components of the torques about that axis that are parallel to that axis.

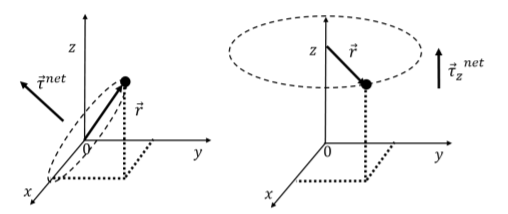
A point particle may be able to rotate about any axis that goes through a point of rotation. The net torque vector on the particle about that point will indicate the direction of the axis about which the particle would rotate. This is illustrated in the left panel of Figure \(\PageIndex{2}\).

Instead, if the particle were constrained to rotate about the \(z\) axis (e.g. if the particle is on a track), then we would use the component of the torque vector that is parallel to the \(z\) axis to describe its motion, as illustrated in the right panel. The \(z\) component of the torque could be determined by using only the components of the forces that lie in the plane perpendicular to the axis, and defining the vector \(\vec r\) from the axis to the particle rather than from the point of rotation to the particle.

Figure \(\PageIndex{2}\): Left panel: a particle rotating about a circle centered at the origin with an axis determined from the net torque vector. Right panel: a particle that is constrained to rotate about the \(z\) axis.

Example \(\PageIndex{1}\)

A force given by \(\vec F=F_x\hat x + F_y \hat y + F_z \hat z\) is exerted at a position \(\vec r=r_x \hat x + r_y \hat y + r_z\hat z\). Calculate the torque about the \(z\) axis as well as the torque about the origin.

Solution

To calculate the torque about the \(z\) axis, we need take the cross-product between the components of the vectors \(\vec r\) and \(\vec F\) that lie in the \(x-y\) plane, since that is the plane perpendicular to the axis of rotation (the \(z\) axis). This gives:

\[\begin{aligned} \vec\tau_z =(r_x \hat x + r_y \hat y) \times (F_x\hat x + F_y \hat y) =(r_xF_y-r_yF_y)\hat z\end{aligned}\]

If instead we want to calculate the torque about the origin, we take the cross-product between the two vectors:

\[\begin{aligned} \vec\tau &=(r_x \hat x + r_y \hat y+ r_z\hat z) \times (F_x\hat x + F_y \hat y+ F_z \hat z)\\[4pt] &=(r_yF_z-r_zF_y)\hat x+(r_zF_x-r_xF_z)\hat y+(r_xF_y-r_yF_y)\hat z\end{aligned}\]

If a particle were located at the given position, the force would cause the particle to (instantaneously) rotate about an axis that goes through the origin and is parallel to the torque vector.

Discussion

This example highlights the difference between calculating the torque about an axis of rotation and determining the torque about a point. When calculating the torque about an axis that goes through the origin, we only consider the components of the vectors \(\vec r\) and \(\vec F\) that are in the plane perpendicular to the axis of rotation. This would correspond to a situation in which the particle is constrained to move in a plane that is perpendicular to the axis of rotation. Instead, if we calculate the torque about the origin, then the torque vector determines the axis of rotation through the origin about which the particle would rotate. In this case, since the axis of rotation is the \(z\) axis, and the point of rotation was the origin, the torque about the \(z\) axis was simply the \(z\) component of the torque calculated about the origin.