11.3: Torque
( \newcommand{\kernel}{\mathrm{null}\,}\)
The torque associated with a force is a mathematical tool to describe how much a particular force will cause a particle (or solid) object to rotate about a given point or a given axis of rotation. A torque is only defined relative to an axis or point of rotation. It never makes sense to say “the torque is ...”, and one should always say “the torque about this axis/point of rotation is ... ”. Angular quantities (torque, angular velocity, angular displacement, etc) are only ever defined relative to a specific axis or point of rotation.
Mathematically, the torque vector from a force, →F, exerted at a position, →r, relative to the axis or point of rotation is defined as:
→τ=→r×→F
Note that the torque from a given force increases if that force is further from the axis of rotation (if →r has a bigger magnitude).
Consider the solid disk of radius, r, depicted in Figure 11.3.1. The disk can rotate about an axis that passes through the center of the disk and that is perpendicular to the plane of the disk. A force, →F, is exerted on the edge of the disk as shown.
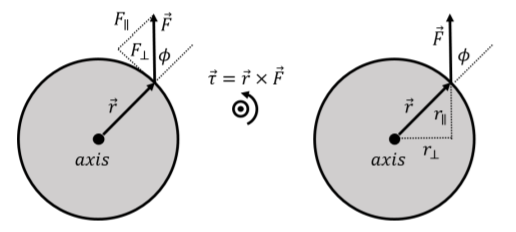
Intuitively, that force will cause the disk to rotate in the counter-clockwise direction. The torque from the force →F about the axis as rotation is given by:
→τ=→r×→F
where the vector →r is perpendicular to the axis of rotation and goes from the axis of rotation to the point where →F is exerted. The direction of the torque vector is out of the page (right hand rule, see Figure 11.3.1), and will thus lead to an angular acceleration that is also out of the page, which corresponds to the counter-clockwise direction, as anticipated.
We can break up the force into components that are parallel (F∥) and perpendicular (F⊥) to the vector →r, as shown on the left panel of Figure 11.3.1. Only the component of the force that is perpendicular to →r will contribute to rotating the disk. Imagine that the force is from a string that you have attached to the perimeter of the disk; if you pull on the string such that the force is parallel to →r, the disk would not rotate. The magnitude of the torque is given by:
τ=rFsinϕ
where ϕ is the angle between →r and →F, as shown in Figure 11.3.1. Fsinϕ is precisely the component of →F that is perpendicular to →r, so we could also write the magnitude of the torque as:
τ=rF⊥
which highlights that only the component of the force that is perpendicular to →r contributes to the torque. Instead of combining the sinϕ with F to obtain F⊥, the component of →F perpendicular to →r, we can instead combine the sinϕ with r in Equation 11.3.1 to obtain r⊥, the component of →r that is perpendicular to →F. This is illustrated in the right panel of Figure 11.3.1. The magnitude of the torque is thus also given by:
τ=r⊥F
The quantity r⊥ is called the “lever arm” of the force about a specific axis of rotation.
Remembering how to maximize the torque about an axis using a pencil
We already know that the greater the force that you apply, the more an object will rotate. Here is an easy way to quickly remind yourself of the two other factors that play a role in whether or not an object will rotate:
Torque about an axis increases if the force is applied further from the axis of rotation.
First, pinch the center of your pencil. Try to make the pencil rotate by pushing right next to where you are pinching. Try making the pencil rotate again, by pushing near the eraser. You should notice that it is much easier to make the pencil rotate by pushing near the eraser, as it is further from the axis of rotation (the pinch).
Torque about an axis is maximized if the force is applied perpendicular to the object.
Next, you should try pushing on the top of the eraser of your pencil, parallel to the pencil. The pencil will not rotate. Now, try pushing on the eraser, but perpendicular to the pencil. In this case, the pencil will rotate.
If you are ever having trouble remembering the factors involved in maximizing torque about an axis, just grab your pencil case and do this quick exercise.
Why is the handle of a door placed on the side of the door that is opposite to the hinges?
- Because it increases the lever arm of a force used to rotate the door about the handle.
- Because it increases the perpendicular component of force used to rotate the door about the hinges.
- Because it increases the lever arm of a force used to rotate the door about the hinges.
- Because it would be inconvenient if the handle were next to the hinges.
- Answer
- C.

