8A: One-Dimensional Motion: Collision Type II
( \newcommand{\kernel}{\mathrm{null}\,}\)
A common mistake one often sees in incorrect solutions to collision type two problems is using a different coordinate system for each of the two objects. It is tempting to use the position of object 1 at time 0 as the origin for the coordinate system for object 1 and the position of object 2 at time 0 as the origin for the coordinate system for object 2. This is a mistake. One should choose a single origin and use it for both particles. (One should also choose a single positive direction.)
We define a Collision Type II problem to be one in which two objects are moving along one and the same straight line and the questions are, “When and where are the two objects at one and the same position?” In some problems in this class of problems, the word “collision” can be taken literally, but the objects don’t have to actually crash into each other for the problem to fall into the “Collision Type II” category. Furthermore, the restriction that both objects travel along one and the same line can be relaxed to cover for instance, a case in which two cars are traveling in adjacent lanes of a straight flat highway. The easiest way to make it clear what we mean here is to give you an example of a Collision Type II problem.
A car traveling along a straight flat highway is moving along at 41.0 m/s when it passes a police car standing on the side of the highway. 3.00 s after the speeder passes it, the police car begins to accelerate at a steady 5.00 m/s^2. The speeder continues to travel at a steady 41.0 m/s. (a) How long does it take for the police car to catch up with the speeder? (b) How far does the police car have to travel to catch up with the speeder? (c) How fast is the police car going when it catches up with the speeder? Solution
The first step in any “Collision Type II” problem is to establish one and the same coordinate system for both objects. Since we are talking about one-dimensional motion, the coordinate system is just a single axis, so what we are really saying is that we have to establish a start line (the zero value for the position variable x) and a positive direction, and we have to use the same start line and positive direction for both objects.
A convenient start line in the case at hand is the initial position of the police car. Since both cars go in the same direction, the obvious choice for the positive direction is the direction in which both cars go.
Next, we establish one and the same time variable t for both objects. More specifically, we establish what we mean by time zero, a time zero that applies to both objects. To choose time zero wisely, we actually have to think ahead to the next step in the problem, a step in which we use the constant acceleration equations to write an expression for the position of each object in terms of the time t. We want to choose a time zero, t=0, such that for all positive values of t, that is for all future times, the acceleration of each object is indeed constant. In the case at hand, the first choice that suggests itself to me is the instant at which the speeder first passes the police car. But if we “start the stopwatch” at that instant, we find that as time passes, the acceleration of the police car is not constant; rather, the police car has an acceleration of zero for three seconds and then, from then on, it has an acceleration of 5.00 m/s^2. So we wouldn’t be able to use a single constant acceleration equation to write down an expression for the position of the police car that would be valid for all times t \ge 0. Now the next instant that suggests itself to me as a candidate for time zero is the instant at which the police car starts accelerating. This turns out to be the right choice. From that instant on, both cars have constant acceleration (which is 0 in the case of the speeder and 5.00 m/s^2 in the case of the police car). Furthermore, we have information on the conditions at that instant. For instance, based on our start line, we know that the position of the police car is zero, the velocity of the police car is zero, and the acceleration of the police car is 5.00 m/s^2 at that instant. These become our “initial values” when we choose time zero to be the instant at which the police car starts accelerating. The one thing we don’t know at that instant is the position of the speeder. But we do have enough information to determine the position of the speeder at the instant that we choose to call time zero. Our choice of time zero actually causes the given problem to break up into two problems: (1) Find the position of the speeder at time 0, and (2) Solve the “Collision Type II” problem.
The solution of the preliminary problem, finding the position of the speeder at time 0, is quite easy in this case because the speed of the speeder is constant. Thus the distance traveled is just the speed times the time.
d=v_st' \nonumber
d=(41.0\dfrac{m}{s})(3.00s) \nonumber
d=123m \nonumber
I used the symbol t' here to distinguish this time from the time t that we will use in the “Collision Type II” part of the problem. We can think of the problem as one that requires two stopwatches: One stopwatch, we start at the instant the speeder passes the police car. This one is used for the preliminary problem and we use the symbol t' to represent the value of its reading. The second one is used for the “Collision Type II” problem. It is started at the instant the police car starts accelerating and we will use the symbol t to represent the value of its reading. Note that d=123m is the position of the speeder, relative to our established start line, at t=0.
Now we are in a position to solve the “Collision Type II” problem. We begin by making a sketch of the situation. The sketch is a critical part of our solution. Sketches are used to define constants and variables. The required sketch for a “Collision Type II” problem is one that depicts the initial conditions.
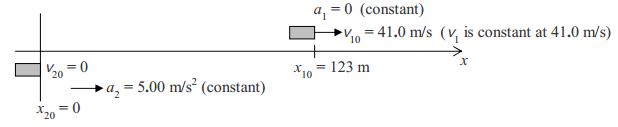
We have defined the speeder’s car to be car 1 and the police car to be car 2. From the constant acceleration equation (the one that gives the position of an object as a function of time) we have for the speeder:

where we have incorporated the fact that a1 is zero. For the police car:
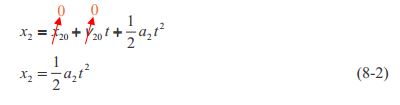
where we have incorporated the fact that x_20=0 and the fact that v_20=0. Note that both equations have the same time variable t. The expression for x_1, gives the position of the speeder’s car for any time t. You tell me the time t, and I can tell you where the speeder’s car is at that time t just by plugging it into equation 8-1. Similarly, equation 8-2 for x_2 gives the position of the police car for any time t. Now there is one special time t, let’s call it t^\ast when both cars are at the same position. The essential part of solving a “Collision Type II” problem is finding that that special time t^\ast which we refer to as the “collision time.” Okay, now here comes the big central point for the “Collision Type II” problem. At the special time t^\ast,
x_1=x_2 \nonumber
We have defined the speeder’s car to be car 1 and the police car to be car 2. From the constant acceleration equation (the one that gives the position of an object as a function of time) we have for the speeder:
This small simple equation is the key to solving every “Collision Type II” problem. Substituting our expressions for x_1 and x_2 in equations 1 and 2 above, and designating the time as the collision time t^\ast we have
x_{10}+v_{10}t^\ast=\dfrac{1}{2}a_2t^{\ast2} \nonumber
This yields a single equation in a single unknown, namely, the collision time t^\ast. We note that t^\ast appears to the second power. This means that the equation is a quadratic equation so we will probably (and in this case it turns out that we do) need the quadratic formula to solve it. Thus, we need to rearrange the terms as necessary to get the equation in the form of the standard quadratic equation ax^2+bx+c=0 (recognizing that our variable is t^\ast rather than x). Subtracting x_{10}+v_{10}t^\ast from both sides, swapping sides, and reordering the terms yields
\dfrac{1}{2}a_2t^{\ast 2}-v_{10}t^\ast-x_{10}=0 \nonumber
which is the standard form for the quadratic equation. The quadratic formula x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a} then yields
t^\ast=\dfrac{-(-v_{10})\pm\sqrt{(-v_{10})^2-4(\dfrac{1}{2}a_2)(-x_{10})}}{2(\dfrac{1}{2}a_2)} \nonumber
which simplifies ever so slightly to
t^\ast=\dfrac{v_{10}\pm\sqrt{v_{10}^2+2a_2x_{10}}}{a_2} \nonumber
Substituting values with units yields:
t^\ast=\dfrac{41.0\dfrac{m}{s}\pm\sqrt{(41.0\dfrac{m}{s})^2+2(5.00\dfrac{m}{s^2})123m}}{5.00\dfrac{m}{s^2}} \nonumber
Evaluation gives two results for t^\ast, namely t^\ast=19.0s and t^\ast=-2.59s. While the negative value is a valid solution to the mathematical equation, it corresponds to a time in the past and our expressions for the physical positions of the cars were written to be valid from time 0 on. Prior to time 0, the police car had a different acceleration than the 5.00\dfrac{m}{s^2} that we used in the expression for the position of the police car. Because we know that our equation is not valid for times earlier that t=0 we must discard the negative solution. We are left with t^\ast=19.0s for the time when the police car catches up with the speeder. Once you find the “collision” time in a “Collision Type II” problem, the rest is easy. Referring back to the problem statement, we note that the collision time itself t^\ast=19.0s is the answer to part a, “How long does it take for the police car to catch up with the speeder?” Part b asks, “How far must the police car travel to catch up with the speeder?” At this point, to answer that, all we have to do is to substitute the collision time t^\ast into equation 8-2, the equation that gives the position of the police car at any time:
x_2=\dfrac{1}{2}a_2t^{\ast2} \nonumber
x_2=\dfrac{1}{2}(5.00\dfrac{m}{s^2})(19.0s)^2 \nonumber
x_2=902m \nonumber
Finally, in part c of the problem statement we are asked to find the velocity of the police car when it catches up with the speeder. First we turn to the constant acceleration equations to get an expression for the velocity of the police car at as a function of time:
v_2=v_{02}+a_2t \nonumber
The velocity of the police car at time zero is 0 yielding: v_2=a_2t \nonumber
To get the velocity of the police car at the “collision” time, we just have to evaluate this at t=t^\ast=19.0s. This yields:
v_2=(5.00\dfrac{m}{s^2})19.0s \nonumber
v_2=95.0\dfrac{m}{s} \nonumber
for the velocity of the police car when it catches up with the speeder.


