3.7: Sample Problems and Solutions
- Page ID
- 19378
Show that one can use Equations 3.2.2 and 3.2.3 to derive the following equation:
\(v^{2}-v_{0}^{2}=2a(x-x_{0})\)
which is independent of time.
- Answer
-
We start with the equations for position and velocity that we derived in this chapter:
\(\begin{aligned} x&=x_{0}+v_{0}t+\frac{1}{2}at^{2} \\[4pt] v&=v_{0}+at \end{aligned}\)
The first equation can be written as:
\((x-x_{0})=v_{0}t+\frac{1}{2}at^{2}\)
Our goal is to find an equation that is independent of time \(t\). We start by isolating \(t\) in our equation for velocity:
\(\begin{aligned} v&=v_{0}t+at \\[4pt] t&=\frac{v-v_{0}}{a} \end{aligned}\)
We then substitute this value of \(t\) into our equation for \((x − x_{0})\):
\(\begin{aligned} (x-x_{0})&=v_{0}t+\frac{1}{2}at^{2} \\[4pt] (x-x_{0})&=v_{0}\left( \frac{v-v_{0}}{a}\right) +\frac{1}{2}a\left( \frac{v-v_{0}}{a} \right)^{2} \end{aligned}\)
We want the left hand side to be \(2a(x − x_{0})\), so we multiply each term by \(2a\):
\(\begin{aligned} 2a(x-x_{0})x&=(2a)v_{0}\left(\frac{v-v_{0}}{a} \right)+(2a)\frac{1}{2}a\left(\frac{v-v_{0}}{a} \right)^{2} \\[4pt] 2a(x-x_{0})&=(2v_{0})a\left(\frac{v-v_{0}}{a} \right)+a^{2}\left( \frac{v-v_{0}}{a} \right)^{2} \\[4pt] 2a(x-x_{0})&=2v_{0}(v-v_{0})+(v-v_{0})^{2} \end{aligned}\)
We distribute \(2v_{0}\) into the brackets. Then we expand the third term and get:
\(\begin{aligned}2a(x-x_{0})&=(2v_{0}v-2v_{0}^{2})+(v_{0}-v^{2})(v_{0}-v^{2}) \\[4pt] 2a(x-x_{0})&=(2v_{0}v-2v_{0}^{2})+(v_{0}^{2}-2v_{0}v+v^{2}) \end{aligned}\)
All that’s left to do is collect like terms, and we get the formula we are looking for:
\(\begin{aligned} 2a(x-x_{0})&=2v_{0}v-2v_{0}^{2}+v_{0}^{2}-2v_{0}v+v^{2} \\[4pt] 2a(x-x_{0})&=(v^{2})+(2v_{0}v-2v_{0}v)+(v_{0}^{2}-2v_{0}^{2}) \\[4pt] 2a(x-x_{0})&=v^{2}-v_{0}^{2} \\[4pt] \therefore v^{2}-v_{0}^{2}&=2a(x-x_{0}) \end{aligned}\)
If you choose a coordinate system such that \(x_{0}\), this equation becomes \(v^{2}−v_{0}^{2}=2ax\).
Rob is riding his bike at a speed of \(8\) m/s. He passes by a velociraptor, as one often does, who is eating by the side of the road. The velociraptor begins chasing him. The velociraptor accelerates from rest at a rate of \(4\) m/s\(^{2}\).
- Assuming it takes \(3\) seconds for the velociraptor to react, how long does it take from the moment Rob passes by for the velicoraptor to catch up to him?
- If there is a safe place \(70\) meters from where Rob passes the velociraptor, will Rob make it there in time to escape being eaten?
- Answer
-
We start by choosing our coordinate system. The solution is simplest if the \(x\) axis is positive in the direction of motion and has an origin at the point where Rob passes the velociraptor. We also choose \(t = 0\) to be the moment the velociraptor starts running.
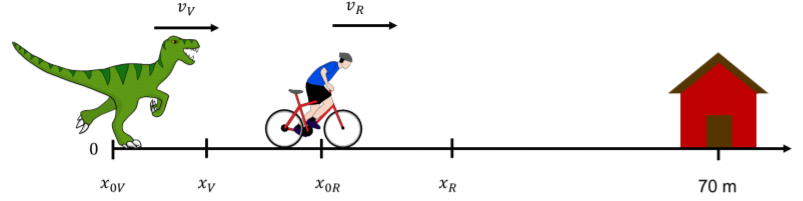
Figure \(\PageIndex{1}\): Rob is being chased by a velociraptor. At \(t=0\), Rob is a distance \(x_{0R}\) from the velociraptor. Safety is \(70\text{m}\) away from the origin. a. What do we mean by “catch up”? It means that Rob and the velociraptor will have the same position at the same time. So, we are interested in the value of \(t\) when \(x_{R} = x_{V}\), where \(x_{R}\) is the position of Rob, and \(x_{V}\) is the position of the velociraptor. We need two equations, one describing Rob’s position and one describing the position of the velociraptor. Rob is moving at a constant velocity, so his position is described by:
\(x_{R}=x_{0R}+v_{R}t\)
The velociraptor has a constant acceleration, so its position is described by:
\(x_{V}=x_{0V}+v_{0v}t+\frac{1}{2}a_{V}t^{2}\)
We can use a table to list the numerical values that we know:
Rob Velociraptor \(x_{0R}=?\) \(x_{0V}=0\text{m}\) \(v_{R}=8\text{m/s}\) \(v_{0V}=0\text{m/s}\) \(a_{V}=4\text{m/s}^{2}\) Table 3.7.1
\(x_{0R}\) is Rob’s position at the instant the velociraptor starts running. The value of \(x_{0R}\) is unknown but can be easily solved for. It takes \(3\) seconds for the velociraptor to react, so at \(t = 0\), Rob has moved \((8\text{m/s}) × (3\text{s}) = 24\text{m} = x_{0R}\) (where we used the formula \(x = vt\)).
Since \(v_{0V} = 0\) (the velociraptor starts running from rest) and \(x_{0V} = 0\) (the velociraptor starts at the origin), we can write our equations for the position as:
\(\begin{aligned} x_{R}=x_{0R}+v_{R}t \\[4pt] x_{V}=\frac{1}{2}a_{V}t^{2} \end{aligned}\)
Remember that we want to find \(t\) when \(x_{R}=x_{V}\). Setting the above equations equal to one another gives:
\(\begin{aligned} x_{R}&=x_{V} \\[4pt] x_{0R}+v_{R}t&=\frac{1}{2}a_{V}t^{2} \\[4pt] \therefore \frac{1}{2}a_{V}t^{2}-v_{R}t-x_{0R}&=0 \end{aligned}\)
which is a quadratic equation for \(t\). Substituting in numerical values, and solving for \(t\):
\(\begin{aligned} \frac{1}{2}(4\text{m/s}^{2})t^{2}-(8\text{m/s})t-(24\text{m})&=0 \\[4pt] 2t^{2}-8t-24&=0 \\[4pt] \therefore t&=\frac{8\pm\sqrt{256}}{4}=6.0\text{s} \end{aligned}\)
Where we chose the positive root of the quadratic, since the time must be a positive quantity. This doesn’t quite give us the answer we want, since we want to know how long it takes the velociraptor to catch up from the moment Rob passes by. We thus have to add the \(3\) s reaction time, giving a total time of \(9\) s.
b. We can use this solution to figure out whether Rob makes it to safety. The velociraptor catches up after \(9\) seconds. In \(9\) seconds, Rob has traveled a distance of \((8 \text{m/s}) × (9 \text{s}) = 72 \text{m}\). The shelter is only \(70\text{m}\) away, so Rob gets to safety in time!
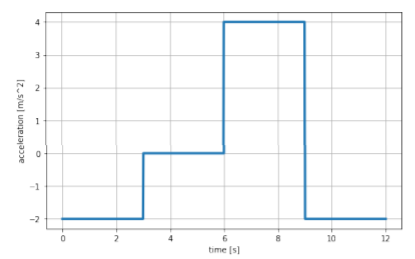
Figure \(\PageIndex{2}\) shows a graph of the acceleration, \(a(t)\), of a particle moving in one dimension. Draw the corresponding velocity and position graphs. Assume that \(v(0) = 0\) and \(x(0) = 0\), and be as quantitative as possible.
- Answer
-
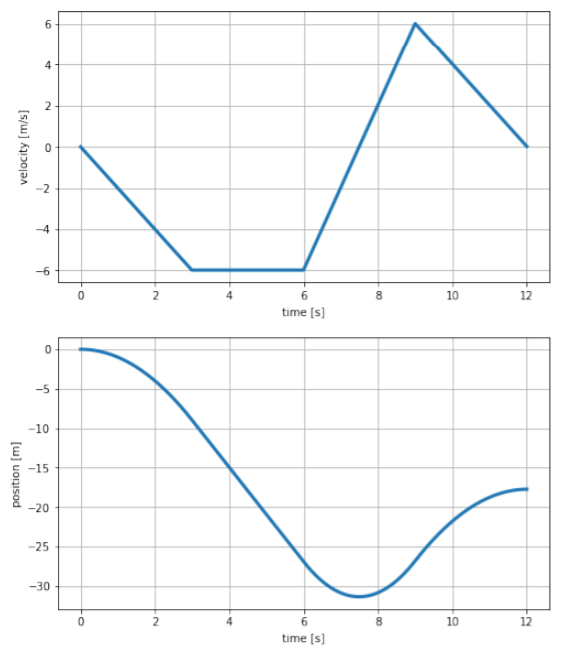
Figure \(\PageIndex{3}\): Graphs of \(v(t)\) and \(x(t)\) corresponding to the acceleration versus time graph given in the question. We start by drawing the graph of \(v(t)\) from the graph of \(a(t)\). Solutions may vary, but a few key features must be present:
- Between \(t = 0\) s and \(t = 3\) s, the velocity decreases linearly, since the acceleration is constant and negative.
- Between \(t = 3\) s and \(t = 6\) s, the velocity remains constant, since the acceleration is zero.
- Between \(t = 6\) s and \(t = 9\) s, the velocity increases linearly, since the acceleration is positive. Since the acceleration is twice as large as in the first interval, the velocity increases at twice the rate that it decreased in the first interval. The object changes direction during this interval, since the velocity changes sign.
- Between \(t = 9\) s and \(t = 12\) s, the velocity decreases linearly with the same rate as in the first interval, and is zero at the end of this interval.
We can get the graph of \(x(t)\) from the graph of \(v(t)\). The graph of \(x(t)\) should have these features:
- Between \(t = 0\) s and \(t = 3\) s, position decreases quadratically, as the velocity is negative and the decreasing.
- Between \(t = 3\) s and \(t = 6\) s, position decreases linearly, since the velocity is negative and constant.
- Between \(t = 6\) s and \(t = 9\) s, the position continues to decrease, but at a lesser rate the velocity approaches zero. When the velocity is zero, the position stop changing, and starts to increase quadratically as the velocity becomes positive and increasing.
- Between \(t = 9\) s and \(t = 12\) s, the position continues to increase, but at a lesser rate as the velocity decreases back to zero.

