6.1: Statics
( \newcommand{\kernel}{\mathrm{null}\,}\)
When using Newton’s Laws to model an object, one can identify two broad categories of situations: static and dynamic. In static situations, the acceleration of the object is zero. By Newton’s Second Law, this means that the vector sum of the forces (and torques, as we will see in a later chapter) exerted on an object must be zero. In dynamic situations, the acceleration of the object is non-zero.
For static problems, since the acceleration vector is zero, we can choose a coordinate system in a way that results in as many forces as possible being aligned with the axes (so that we minimize the number of forces that we need to break up into components).
You push horizontally with a force →F on a box of mass m that is resting against a vertical wall, as shown in Figure 6.1.1. The coefficient of static friction between the wall and the box is μs. What is the minimum magnitude of the force that you must exert for the box to remain stationary?
Solution
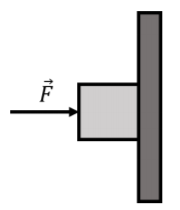
Since the acceleration of the box is zero, the vector sum of the forces exerted on the box is zero. We start by identifying the forces exerted on the box; these are:
- →F, the horizontal force that you exert on the box.
- →Fg, the weight of the box, with magnitude mg.
- →N, a normal force exerted by the wall on the box. The force is in the horizontal direction, in the opposite direction to →F.
- →fs, a vertical force of static friction between the wall and the box. The force points upwards as the “impeding motion” of the block is downwards. The force will have at most a magnitude of fs≤μsN, since the force of static friction depends on the other forces exerted on the object.
The forces are shown in the free-body diagram in Figure 6.1.2, along with our choice of coordinate system which was chosen so that all forces are either in the x or y direction.
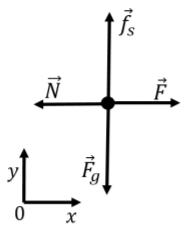
The x component of Newton’s Second Law is:
∑Fx=F−N=0∴N=F
which tells us that the normal force exerted by the wall has the same magnitude as the applied force, →F. The y component of Newton’s Second Law is:
∑Fy=fs−Fg=0∴fs−mg=0∴fs=mg
which tells us that the force of friction must have the same magnitude as the weight. This makes sense, since they are the only forces with components in the y direction, and thus, they must cancel each other out.
The force of friction will be less than or equal to μsN, and thus less than or equal to μsF, since →F and →N have the same magnitude (from the x component of Newton’s Second Law). Furthermore, since fs=mg, we can write:
fs≤μsF∴mg≤μsF∴mgμs≤F
which gives us the condition that F≥mg/μs, and thus the minimum magnitude of F in order to keep the box from sliding down.
Although we used the lesser than or equal to sign in the above equations, we could have used an equal sign if we were confident that the force of friction has its maximal magnitude, fs=μsN. The maximal magnitude of the force of friction is proportional to the force that we exert (since N=F); if we want to exert the least amount of force F, then we need the force of friction to be equal to its maximal magnitude which needs to be equal to the weight of the box.
Discussion
This model for the minimal required force makes sense because:
- The dimension of mg/μs is force.
- If the mass of the box is increased, then one needs to push harder against the box to keep it up.
- If the coefficient of static friction, μs, is increased, one does not need to push as hard.

