9.2: Newton’s Universal Theory of Gravity
- Page ID
- 19422
Newton supposedly gained insight into the gravitational force by observing an apple falling from a tree and concluding that if it is the same force that makes apples fall at sea level and at the top of a mountain, perhaps that force can be exerted all the way up to the moon. It is rather remarkable that Newton was able to make the connection between falling apples and the motion of the moon around the Earth to find a single theory to describe both situations.
We should be clear that the theory of gravity is a different theory than Newton’s “Laws of Motion” (Newton’s Three Laws). The Laws of Motion introduce the concepts of force and inertial mass, and prescribe how to use those concepts in order to model motion using kinematics. Newton’s Universal Theory of Gravity is a theory that describes the force of gravity that two bodies with (gravitational) mass exert on each other.
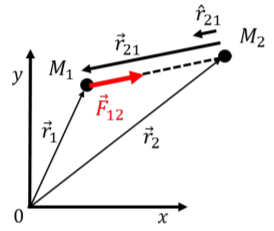
Newton’s Universal Theory of Gravity states that if two bodies, with masses \(M_1\) and \(M_2\), located at positions \(\vec r_1\) and \(\vec r_2\), respectively, are separated by a distance, \(r\), then \(M_2\) will exert an attractive force on \(M_1\), \(\vec F_{12}\), given by:
\[\begin{aligned} \vec F_{12}=-G\frac{M_1M_2}{r^2}\hat r_{21}\end{aligned}\]
where \(\hat r_{21}\) is the unit vector from \(M_2\) to \(M_1\):
\[\begin{aligned} \vec r_{21} &= \vec r_2 - \vec r_1\\[4pt] \hat r_{21} &= \frac{1}{r} \vec r_{21}\end{aligned}\]
as shown in Figure \(\PageIndex{1}\). \(\vec F_{12}\) should be read as “the force on body 1 from body 2”. \(G=6.67\times 10^{-11}\text{Nm}^{2}/\text{kg}^{2}\) is Newton’s Universal Constant of Gravity. It should be noted that Newton’s theory for the force of gravity written in this form only applies to either point masses (separated by a distance \(r\)) or spherical bodies whose centers are separated by a distance \(r\) that is larger than the radius of either sphere.
Originally, Newton argued that the force of gravity would be proportional to the masses of the bodies, and inversely proportional to the square of the distance between them:
\[\begin{aligned} F_{12}\propto \frac{M_1M_2}{r^2}\end{aligned}\]
and \(G\) is simply the constant of proportionality.
Because of Newton’s Third Law, body 1 exerts a force on body 2 that is equal in magnitude but opposite in direction:
\[\begin{aligned} \vec F_{12} = -\vec F_{21}\end{aligned}\]
Calculate the magnitude of the force of gravity between yourself and a person standing \(50\text{cm}\) from you and compare that to your weight at the surface of the Earth (the force of gravity exerted by the Earth on you).
Solution
If we assume that the two people have a mass of \(50\text{kg}\), the force of gravity exerted by one on the other, if they are separated by \(50\text{cm}\), is given by:
\[\begin{aligned} F=G\frac{M_1M_2}{r^2}=(6.67\times 10^{-11}\text{Nm}^{2}/\text{kg}^{2})\frac{(50\text{kg})(50\text{kg})}{(0.5\text{m})^2}=6.67\times 10^{-7}\text{N}\end{aligned}\]
This is a very small force, compared to their weight, \(F_g\):
\[\begin{aligned} F_g=M_1g=(50\text{kg})(9.8\text{N/kg})=490\text{N}\end{aligned}\]
which is approximately 700 million times bigger.
Discussion
The force of gravity is a very weak force when compared to other forces in Nature, such as the electric force between two charges. Newton’s Universal Constant of Gravity is very small, so the force of gravity between two objects is very small unless either of the masses involved are very large, or the distance between them is very small. In general, when modeling the motion of objects on the Earth, it is generally safe to ignore the forces of gravity between objects and only include their weight (the force of gravity from the Earth).
The radius of the Earth is \(6371\) km. What is the order of magnitude of the Earth’s mass?
- \(10^{24}\text{kg}\)
- \(10^{18}\text{kg}\)
- \(10^{19}\text{kg}\)
- \(10^{21}\text{kg}\)
Not enough information.
- Answer
Determine the constant in Kepler’s Third Law for planets orbiting the Sun, namely the value of the ratio:
\[\begin{aligned} \frac{s^3}{T^2}\end{aligned}\]
where \(s\) is the semi-major axis and \(T\) is the orbital period.
Solution
Since Kepler’s Third Law holds for any body orbiting the Sun, we can easily determine the ratio by considering a planet of mass \(m\) in a circular orbit of radius \(R\) centerd about the Sun. The semi-major axis of the orbit is equal to the radius of the orbit for a circular orbit (\(s=R\)).
If the planet is in a circular orbit about the Sun, its speed, \(v\), will be constant, by Kepler’s Second Law, and it will thus be executing uniform circular motion. The only force exerted on the planet is the force of gravity exerted by the Sun. Thus the force of gravity must be equal to the mass of the planet times its radial (centripetal) acceleration, \(a_R\), which is given by:
\[\begin{aligned} a_R=\frac{v^2}{R}\end{aligned}\]
Newton’s Second Law for the planet can be written as:
\[\begin{aligned} \sum F = F_g &= ma_R\\[4pt] G\frac{Mm}{R^2}&=m\frac{v^2}{R}\\[4pt] G\frac{M}{R}&=v^2\end{aligned}\]
where \(M\) is the mass of the Sun. The speed of the planet is given by the circumference of the orbit divided by the orbital period \(T\), since it is constant:
\[\begin{aligned} v=\frac{2\pi R}{T}\end{aligned}\]
Re-arranging the equation from Newton’s Second Law:
\[\begin{aligned} G\frac{M}{R}&=v^2\\[4pt] G\frac{M}{R}&=\frac{4\pi^2 R^2}{T^2}\\[4pt] \therefore \frac{R^3}{T^2}&=G\frac{M}{4\pi^2}\end{aligned}\]
Thus, we find that the ratio of the cube of the orbital radius to the period squared is a constant that depends only on the mass of the Sun, which will then be the same for all planets (as it does not depend on, say, the mass of the planet that we considered).
Discussion
The relation above can, for example, be used to determine the mass of the Sun, since we can use geometry to determine the semi-major axis for the orbit of a planet, as Kepler did with the data from Tycho Brahe.
The acceleration due to Earth’s gravity depends on the force that the Earth exerts on an object. Using the Earth’s mass and radius, determine the acceleration of falling objects due to Earth’s gravity at the surface of the Earth. Also, determine the altitude where the acceleration due to Earth’s gravity is half of that at the Earth’s surface.
Solution
We can find the acceleration due to Earth’s gravity by determining the acceleration of a mass \(m\) upon which gravity is the only acting force. In other words, we model an object that is in free-fall a distance \(R\) away from the center of the Earth. Newton’s Second Law can be used in one dimension (corresponding to the direction that connects the falling mass to the center of the Earth):
\[\begin{aligned} \sum F &= G\frac{Mm}{R^2}=ma\\[4pt] \therefore a&=G\frac{M}{R^2}\end{aligned}\]
where \(M=5.97\times 10^{24}\text{kg}\) is the mass of the Earth. At the surface of the Earth, \(R=R_\oplus=6.371\times 10^{6}\text{m}\):
\[\begin{aligned} a&=G\frac{M}{R_\oplus^2}=(6.67\times 10^{-11}\text{Nm}^{2}/\text{kg}^{2})\frac{(5.97\times 10^{24}\text{kg})}{(6.371\times 10^{6}\text{m})^2}\\[4pt] &=9.81\text{m/s}^{2}\end{aligned}\]
which, of course, is the value of \(g\) that we have been using so far for the acceleration due to gravity near the surface of the Earth. To find the altitude at which this is reduced by half, we first find the value of \(R\) that corresponds to this acceleration:
\[\begin{aligned} \frac{1}{2}G\frac{M}{R_\oplus^2}&=G\frac{M}{R^2}\\[4pt] \therefore R &=\sqrt{2}R_\oplus = 9.0\times 10^{6}\text{m}\end{aligned}\]
which corresponds to an altitude of \(h=R-R_\oplus=2640\text{km}\), well above the Earth’s atmosphere.
Discussion
The acceleration of falling objects decreases as one moves further from the center of the Earth. It is thus an approximation to assume that \(g\) is a constant, although in most cases this is a very good approximation. In practice, the value of \(g\) will depend both on the distance from the center of the Earth and the composition (density) of the material in the Earth’s crust below where \(g\) is being measured. Precise measurements of \(g\) have bee used to determine the composition of the Earth’s crust and to search for mineral and oil deposits.
Weight and apparent weight
You have probably seen images of astronauts floating around the International Space Station (ISS) or other orbiting vessels, and heard of the term “weightlessness” to describe their motion. The ISS is in orbit at an altitude of approximately \(400\text{km}\), where the force of Earth’s gravity is far from negligible (in Example 9.2.3 we showed that one needs to go to an altitude of \(2640\text{km}\) for the force to be reduced by half of that at the surface of the Earth). The contradiction between being weightless and the fact that weight is not zero is resolved by understanding that the popular term “weightless” is imprecise from a physics perspective.
The correct term to use from a physics perspective is to say that the apparent weight of the astronauts is zero when they are floating around. Weight is the magnitude of the force of gravity exerted by the Earth. Apparent weight is, for example, the force that one measures when standing on a spring scale, which is equal to the normal force exerted by the spring scale on the person. Apparent weight could also be determined by the tension in a string from which a person is suspended. The apparent weight is the sum of the forces exerted on a person minus the force of gravity. If gravity is the only force exerted on a person (or object), that person’s apparent weight is zero, which is what is popularly called being weightless.
One way to feel weightless is when you are in free-fall (e.g. the first few seconds of a parachute jump from an airplane). One can think of being in orbit as continuously falling towards the center of the Earth, but with an initial velocity in a direction such that you never actually collide with the Earth. The feeling of weightlessness will occur any time that the only force exerted on you is the force of gravity. If you are in a spacecraft in any orbit and the only force on the spacecraft is from gravity (i.e. no rockets or wings are exerting any forces), then everything in the spacecraft will have the same acceleration, since gravity is the only force acting on anything in the spacecraft, and it will appear that everything is just floating. To an outside observer, it would be clear that the spacecraft and its contents are all accelerating.
Effects of Earth’s rotation
Earth’s rotation affects the apparent weight of objects near the Earth’s surface. Consider a person standing on a spring scale at the North pole (top free-body diagram in Figure \(\PageIndex{2}\)). The only two forces exerted on the person are their weight, \(\vec F_g\), and the normal force, \(\vec N\), exerted by the spring scale. Since the person is not accelerating, the normal force and the weight have the same magnitude and opposite directions. The scale will thus read the actual weight of the person1.
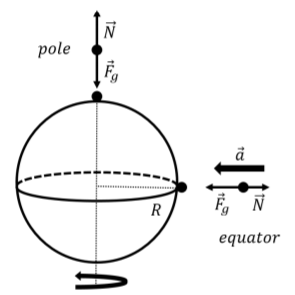
Consider, instead, a person standing on a spring scale at the equator (Figure \(\PageIndex{2}\)). That person is accelerating because they are undergoing uniform circular motion as they rotate along with the Earth. Again, the only forces acting on the person are their weight and the normal force exerted by the scale. The sum of the forces must now be equal to the person’s mass, \(m\), times the radial acceleration, \(a_r\), that is necessary for them to follow the surface of the Earth as the Earth rotates about its axis. Newton’s Second Law allows us to find the magnitude of the normal force acting on the person:
\[\begin{aligned} \sum F &= F_g-N=ma_r=m\frac{v^2}{R}\\[4pt] \therefore N &= F_g - m\frac{v^2}{R}\\[4pt] &=G\frac{Mm}{R^2} - m\frac{v^2}{R}\\[4pt] &=m\left(G\frac{M}{R^2} - \frac{v^2}{R} \right)\\[4pt] &=m\left(g - \frac{v^2}{R} \right)\end{aligned}\]
where \(M\) is the mass of the Earth, \(R\) is the radius of the Earth, and \(v\) is the speed at the surface of the Earth due to the Earth’s rotation. In the last line, we used the result from Example 9.2.3 where we determined the value of \(g\) in terms of the mass and radius of the Earth.
We see that the normal force is reduced compared to what it would be if the Earth were not rotating (\(v=0\)) or if one is standing at one of the poles. Your apparent weight, which you can measure by standing on a spring scale, is thus smaller at the equator than it is at the poles. The quantity in parenthesis can be thought of as a modified or “effective” value of \(g\) at the equator.
What is the effective value of \(g\) at the equator?
- \(9.80 \text{m/s}^2\)
- \(9.78 \text{m/s}^2\)
- \(9.70 \text{m/s}^2\)
- \(9.51 \text{m/s}^2\)
- Answer
If you are circling the Earth a distance \(R\) from the center of the Earth at a constant speed \(v\), it is possible for your apparent weight to be zero. Imagine standing on a scale in an aircraft that is circling the Earth and measuring your apparent weight with the spring scale. As the speed of the aircraft increases, your apparent weight, \(N\), decreases according to the formula that we just found:
\[\begin{aligned} N=m\left(G\frac{M}{R^2} - \frac{v^2}{R} \right)\end{aligned}\]
At a certain speed, \(v\), your apparent weight is zero and you feel weightless:
\[\begin{aligned} G\frac{M}{R^2} &= \frac{v^2}{R}\\[4pt] \therefore v&= \sqrt{G\frac{M}{R} }\end{aligned}\]
This speed corresponds to a centripetal acceleration that is exactly equal to that due to gravity. This makes sense, since gravity is the only force that is acting on you (the normal force is now zero), which is exactly what we call being in orbit.
Earth’s rotation has some interesting consequences for stationary objects. At any position on Earth that is not at the equator or the poles, the sum of the forces on any stationary object (meaning stationary relative to the Earth’s surface) cannot be zero. This is because the object must rotate along with the Earth, so the net force on the object must point toward the center of the circle about which that location on Earth is rotating.
Take, for example, a plumb line, which consists of a mass hanging from a string. The two forces acting on the mass are gravity and tension. The force of gravity must point towards the center of the Earth. We would expect that the force of tension, and therefore the string, would point directly away from the center of the Earth. However, we find that if the plumb line is located at some angle \(\theta\) from the equator (but not at the equator or poles), as in Figure \(\PageIndex{3}\), then the string will point slightly away from the center of the Earth. In order for the mass to remain stationary relative to the ground, it must rotate along with the Earth (radius \(R\)) around a circle of radius \(R\cos\theta\). Thus, the tension from the string cannot point away from the center of the Earth, because the net force must point towards the center of the circle of radius \(R\cos\theta\).
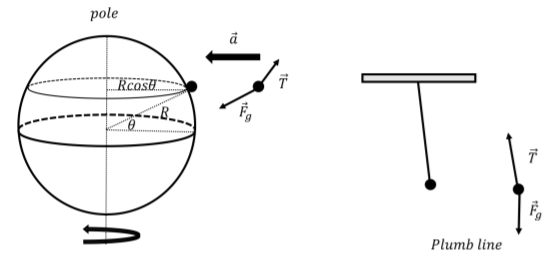
You cut the string of the plumb line. Where does the mass land relative to its initial latitude (the angle \(\theta\) in Figure \(\PageIndex{3}\))?
- At the same latitude.
- Closer to the nearest pole.
- Closer to the equator.
- Answer
The gravitational field
The gravitational force exerted on a mass \(m\) by a mass \(M\) can be written as:
\[\begin{aligned} \vec F(\vec r) = -G\frac{Mm}{r^2}\hat r\end{aligned}\]
if we define a coordinate system with the origin located at the center of mass \(M\) so that \(\vec r\) is the position of \(m\) relative to \(M\). We can define the “gravitational field”, \(\vec g(\vec r)\), at position, \(\vec r\), due to the presence of mass \(M\) as the gravitational force per unit mass exerted by \(M\):
\[\vec g(\vec r)=\frac{\vec F(\vec r)}{m}=-G\frac{Mm}{r^{2}}\hat r\]
The word “field” is just a mathematical term for a function that depends on position. Since \(\vec g(\vec r)\) is a vector, we would refer to it as a “vector field”.
Defining the gravitational field makes it easy to calculate the force of gravity from \(M\) on any mass \(m\):
\[\begin{aligned} \vec F_g = m\vec g(\vec r)\end{aligned}\]
At the surface of the Earth, the magnitude of the gravitational field is given by:
\[\begin{aligned} g(R_\oplus)=\frac{GM}{R_\oplus^2}=9.81\text{N/kg}\end{aligned}\]
where \(R_\oplus\) is the radius of the Earth. Of course, this also corresponds to the acceleration of objects in free-fall near the surface of the Earth, which we can find from Newton’s Second Law:
\[\begin{aligned} \sum \vec F &= \vec F_g = m\vec a\\[4pt] m\vec g(R_\oplus)&= m\vec a\\[4pt] \therefore \vec a &= \vec g(R_\oplus)\end{aligned}\]
but we see here why it more precise to refer to \(g\) as the “magnitude of the gravitational field at the surface of the Earth” rather than “the acceleration due to Earth’s gravity”. It is also worth noting that the two are only equal if the gravitational mass (on the left of the equation in the second line) is the same as the inertial mass (on the right of the equation). The gravitational mass is the mass that appears in the gravitational force defined by Newton, whereas the inertial mass is the mass that appears with the acceleration in Newton’s Second Law.
Two small objects with different masses, \(m_1\) and \(m_2\), are located a distance \(r\) from a nearby star. What can you say about the magnitude of the gravitational field and the magnitude of the gravitational force on \(m_1\) and \(m_2\)?
- The field is different and the forces are different.
- The field is different but the forces are the same.
- The field is the same but the forces are different.
- The field is the same and the forces are the same.
- Answer
Suppose that there are two large mass bodies, \(M_1\) and \(M_2\), and a smaller mass body, \(m\). We can calculate the net gravitational force on \(m\) by summing the gravitational force vectors from \(M_1\) and \(M_2\) separately. If the gravitational fields from \(M_1\) and \(M_2\) are given by \(\vec g_1(\vec r)\) and \(\vec g_2(\vec r)\), respectively, then the total gravitational force on \(m\) is given by:
\[\begin{aligned} \vec F &= m\vec g_1(\vec r) + m\vec g_2(\vec r)=m(\vec g_1(\vec r)+\vec g_2(\vec r))\\[4pt] &=m \vec g(\vec r)\end{aligned}\]
where we have introduced the total gravitational field:
\[\begin{aligned} \vec g(\vec r) = \vec g_1(\vec r)+\vec g_2(\vec r)\end{aligned}\]
In other words, if there are multiple bodies that result in a non-negligible force of gravity, we can calculate their gravitational fields independently and sum them together to define a net gravitational field, \(\vec g(\vec r)\), that models the net force of gravity from all of the bodies. The net gravitational force on a new body of mass \(m'\) is then simply given by \(m'\vec g(\vec r)\), and we do not need to add any more vectors together. For example, when calculating the motion of satellites that can be influenced by the force of gravity from both the Earth and the Moon, we simply need to calculate the net gravitational field from the Earth and Moon, and the motion of any satellite can then be modeled using that net gravitational field.
There are two planets with equal mass located a distance \(d\) apart. Position \(A\) is located midway between the two planets. Position \(B\) is located a distance \(d/2\) from one of the planets, in the position shown in Figure \(\PageIndex{4}\). How does the field at \(A\) compare to the field at \(B\)?
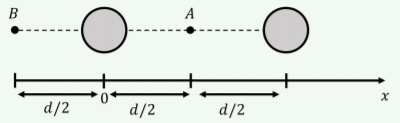
- The magnitude of the field is the same at \(A\) and \(B\).
- The magnitude of the field is greater at \(A\) than at \(B\).
- The magnitude of the field is greater at \(B\) than at \(A\).
- Answer
Gauss’ Law
Newton’s Universal Theory of Gravity postulates that the force of gravity between two bodies decreases as the squared of the distance between those two bodies. Using the terminology of a field, we would say that the strength of the gravitational field from an object decreases as the inverse of the square of the distance to that object. This is an example of a what we generally call an “inverse-square law”. The electric force between two charges is also given by an inverse-square law, and we now understand that these forces behave as if they were “transmitted” by waves or particles.
If a force is given by an inverse-square law, then Gauss’ Law gives a way to determine the strength of the field that is associated with that force. In the case of gravity, Gauss’ Law states that:
\[\begin{aligned} \oint \vec g(\vec r) \cdot d\vec A = 4\pi G M^{enc}\end{aligned}\]
where the integral on the left is an integral over a “closed surface” that completely surrounds the mass for which we want to determine the gravitational field. To evaluate the integral, imagine taking a closed surface, \(S\), that surrounds the mass. The vector \(d\vec A\) is defined as the vector that goes with a small element of that surface and points outwards from the closed surface. The magnitude of the vector is equal to the area of that small surface (\(dA\)), as illustrated in Figure \(\PageIndex{5}\). You can then take the scalar product of \(d\vec A\) with the gravitational field, \(\vec g(\vec r)\), at that point on the surface. If you sum all of those scalar products, you get the value of the integral on the left. Gauss’ Law states that the value of that integral is equal \(4 \pi G\) times the total mass that is enclosed by the surface.
If you want to know if a surface is closed, ask yourself if you could put water inside the surface and not be worried about it spilling out. For example, if you put water in a sphere or a cube , the water would not spill out even if you shook it around, so they are closed surfaces. A flat square is an open surface because there is no “inside” to even put the water in. A bowl is an open surface because, though you can put water in it, the water could spill out.
We will go into more detail about Gauss’ Law when we cover electromagnetism, but it is worth seeing how to use it in a simple scenario. Figure \(\PageIndex{5}\) shows a spherical body of mass \(M\) and radius \(R\) for which we would like to determine the value of the gravitational field at a distance \(r\) from the center of the body.
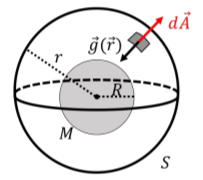
To do so, we draw a “Gaussian surface”, \(S\), that is a sphere with a radius \(r\), and centered about the body. At any point on the surface, the area element vector \(d\vec A\) points away from the center of the spherical surface. The gravitational field vector, \(\vec g(\vec r)\) will always point towards the center of the spherical surface, as illustrated. Furthermore, by symmetry, the magnitude of \(\vec g(\vec r)\) is constant along the whole Gaussian surface. Thus, the scalar product \(\vec g(\vec r) \cdot d\vec A=-g(r)dA\) everywhere along the surface (it is negative because the two vectors are anti-parallel). The integral is thus given by:
\[\begin{aligned} \oint \vec g(\vec r) \cdot d\vec A = -g(r)\oint dA \end{aligned}\]
where we factored \(g(r)\) out of the integral, since the magnitude of \(\vec g(\vec r)\) is constant for all of the area elements \(dA\) on the sphere. Remember that an integral is a sum. The integral \(\oint dA\) thus means “sum all of the area elements \(dA\) over the entire surface \(S\)”. Thus, the integral is the total area of the spherical surface \(S\)2:
\[\begin{aligned} \oint \vec g(\vec r) \
d\vec A = -g(r)\oint dA =-g(r)(4\pi r^2)\end{aligned}\]
Inserting this into Gauss’ Law, we find:
\[\begin{aligned} \oint \vec g(\vec r) \cdot d\vec A &= 4\pi G M^{enc}\\[4pt] -g(r)(4\pi r^2) &= 4\pi G M^{enc}\\[4pt] \therefore g(r) &= - \frac{GM}{r^2}\end{aligned}\]
where \(M^{enc}=M\) is the total mass enclosed by the Gaussian surface (in this case, the entire mass \(M\) is enclosed). This is of course the result that we expected and obtained earlier from Newton’s formulation. Note that Gauss’ Law is only easy to use if the system is highly symmetric (e.g. spherically symmetric), and that it does not give the direction of the field vector, which must be obtained from symmetry arguments.
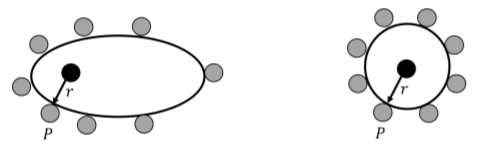
Here’s an analogy to describe Gauss’s Law for gravity: A famous celebrity is doing an event, and they attract a certain number of fans who want to get as close to the celebrity as possible. You put up a barricade around the celebrity. The gravitational field is represented by how crowded it is somewhere along the barricade. If a second celebrity is at the event, they will attract their own fans, so there will be more people around the barricade. The number of celebrities is kind of like the enclosed mass \(M^{enc}\).
A photographer is coming to the event, and you told him to stand at some location that is a distance \(r\) from the celebrities. The photographer wants to know how crowded it will be when he is standing behind the barricade at that location. Gauss’s law gives us a way to figure this out. If you know which celebrities are at the event (\(M^{enc}\)), you can determine how many people will be there (this is like finding \(4\pi GM^{enc}\)). Then, if you can build a barricade such that the fans are evenly distributed around it, and you know how long that barricade is (\(\oint dA\)), you can easily calculate how crowded it will be at some point along the barricade (you can just divide the number of people by the length of the barricade). The barricade represents our Gaussian surface and, like a Gaussian surface, it can be whatever shape we want as long as it encloses the celebrities and passes through the point we are interested in. If we want to make sure the people are spread out evenly, the shape of the barricade is going to depend on the specific case. Let’s take the example of our single spherical body. This is analagous to having one celebrity at the event.
Figure \(\PageIndex{6}\) shows two possible barricades we could build. Although we can technically build the barricade on the left, it doesn’t help us because the areas closer to the celebrity will be more crowded. Instead, we want to build the barricade on the right, which is a circle of radius \(r\), because the fans are evenly spread out. This is why we use a spherical Gaussian surface when we’re considering the field due to a spherical body - at any point a distance \(r\) from the body, the field will be the same. (Note: Remember that, unlike the barricade, the Gaussian surface isn’t a physical thing, so it won’t affect the gravitational field. It is just a mathematical tool that allows us to take advantage of what the field already looks like.)
We can also use Gauss’ Law to determine the gravitational field inside of the body of mass \(M\) and radius \(R\). This is illustrated in Figure \(\PageIndex{7}\), which shows a spherical Gaussian surface of radius \(r\) that is inside of the body of mass \(M\).
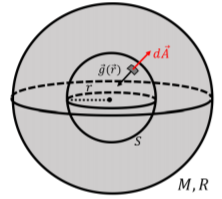
The gravitational field inside of the body of mass \(M\) is also symmetric and constant in magnitude across the whole surface, so that the integral is the same as before:
\[\begin{aligned} \oint \vec g(\vec r) \cdot d\vec A=-g(r)(4\pi r^2)\end{aligned}\]
However, in order to use Gauss’ Law, we need to determine the mass of the body that is enclosed within the spherical surface, which will be less than \(M\). If we assume that the mass density, \(\rho\), of the object is constant (the body is made of a uniform material), then the density is simply the mass of the object over its volume:
\[\begin{aligned} \rho = \frac{M}{\frac{4}{3}\pi R^3}\end{aligned}\]
The amount of mass enclosed by the spherical surface of radius \(r\) is the density multiplied by the volume of a sphere of radius \(r\):
\[\begin{aligned} M^{enc} = \rho \frac{4}{3}\pi r^3 = M\frac{r^3}{R^3}\end{aligned}\]
Applying Gauss’ Law, we can now find the magnitude of the gravitational field inside of the spherical body at a distance \(r\) from the center:
\[\begin{aligned} \oint \vec g(\vec r) \cdot d\vec A &= 4\pi G M^{enc}\\[4pt] -g(r)(4\pi r^2) &= 4\pi G M\frac{r^3}{R^3}\\[4pt] \therefore g(r) &= - \frac{G M}{R^3}r\end{aligned}\]
And we find that, inside a uniform spherical body of mass \(M\), the gravitational field increases linearly with radius as one moves out from the center. At the center of the body, the gravitational field is zero.
What can you say about the magnitude of the gravitational field inside a spherical shell of mass \(M\)?
- It increases as you move out from the center of the spherical shell.
- It decreases as you move out from the center of the spherical shell.
- It is equal to zero.
- It is nonzero and constant in magnitude.
- Answer

