9.3: Gravitational potential energy
( \newcommand{\kernel}{\mathrm{null}\,}\)
Consider a large spherical body of mass M with a coordinate system whose origin coincides with the center of the spherical body (for example, the large body could be the Earth). The force, →F(→r) on a body of mass m (for example, a satellite), located at a position →r is then given by:
→F(→r)=−GMmr2ˆr=−GMmr3→r
where in the second equality, we use the fact that the unit vector in the direction of →r is simply the vector →r divided by its magnitude. We can write the force out in Cartesian coordinates:
→r=xˆx+yˆy+zˆzr=√x2+y2+z2=(x2+y2+z2)12∴→F(x,y,z)=−GMm(x2+y2+z2)32(xˆx+yˆy+zˆz)
Mathematically, this is equivalent to the force that we considered in Example 8.1.2 of Chapter 8, which we showed was a conservative force. The force of gravity in Newton’s theory is thus a conservative force, for which we can determine a potential energy function.
In order to determine the gravitational potential energy function for the mass m in the presence of a mass M, we calculate the work done by the force of gravity on the mass m over a path where the integral for work will be “easy” to evaluate, namely a straight line. Figure 9.3.1 shows such a path in the radial direction, r, over which it will be easy to calculate the work done by the force of gravity from mass M when mass m moves from being a distance rA to a distance rB from the center of mass M.
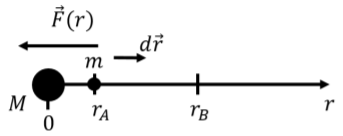
The work done by the force of gravity on m in going from rA to rB is given by:
W=∫rBrA→F(r)⋅d→r=∫rBrA(−GMmr2ˆr)⋅d→r=∫rBrA−GMmr2dr=[GMmr]rBrA=GMmrB−GMmrA
The difference in potential energy in going from position A to position B is given by the negative of the work done by the force:
ΔU=U(rB)−U(rA)=−W=GMmrA−GMmrB
By inspection, we can identify the potential energy function for gravity:
U(r)=−GMmr+C
which is determined only up to a constant, C.
A particularly useful choice of constant is C=0. This corresponds to choosing the potential energy to be zero only when r goes to infinity. That is, the potential energy of mass m is zero only when it is infinitely far away from mass M. The choice of constant C corresponds to the (arbitrary) value of the potential energy when mass m is infinitely far from mass M. When mass m is not infinitely far away, it has negative potential energy (if C=0). This is not a problem! Remember, the only thing that is meaningful is a difference in potential energy, so the specific value of the potential energy has no meaning. The kinetic energy of an object, on the other hand, has to be positive.
Recall that if there are no other forces acting on an object, that object will move in such a way to reduce its potential energy. If the object of mass m is located at some distance r from the object of mass M, the force of gravity will attract m so that r decreases. As r decreases in magnitude, the potential energy becomes more negative (larger in magnitude, but further away from zero), and the potential energy of m will indeed decrease as it accelerates due to the force of gravity.
Mechanical energy with gravity
Unless noted otherwise, we will continue our discussion of gravitational potential energy with the particular choice of constant C=0:
U(r)=−GMmr
Furthermore, we will assume that M is a large body, such as the Earth, which we can consider as fixed, and focus our discussion on describing the motion of mass m (e.g. a satellite). If M is much bigger than m, they will both experience a force of gravity from each other of the same magnitude (Newton’s Third Law), but because M is so much larger, its acceleration will be much smaller (Newton’s Second Law). Thus, it is a good approximation to assume that M is stationary and that only m moves when M>>m.
We can define the total mechanical energy of mass m when it has a speed v (relative to M) and is located at a distance r from the center of mass M:
E=U+K=−GMmr+12mv2
where the kinetic energy term is always positive. If gravity is the only force exerted on mass m, then the mechanical energy, E, as defined above, will be a constant. The mechanical energy of an object can give us insight into the possible motion of the object.
Imagine launching a rocket straight upwards from the surface of the Earth; once all of the fuel has burnt up, the rocket’s mechanical energy becomes constant as the rocket engine stops doing work on the rocket. As soon as the engine stops providing thrust, the rocket will start to slow down as the force of gravity attracts the rocket back to Earth. If the rocket is going fast enough, it will be able to completely escape the Earth’s gravitational pull and travel to infinity (we assume that there are no other planets or the Sun, just the Earth exists!). If, on the other hand, the rocket’s speed is too low, it will eventually stop and fall back to Earth. This is the same thing that happens to you when you try to jump vertically. If you could jump hard enough, you would be able to escape the Earth’s gravitational pull!
In terms of mechanical energy, we can ask ourselves if the mechanical energy of the rocket is large enough to escape the Earth’s gravitational pull. Specifically, we can ask ourselves what the value of the rocket’s kinetic energy would be when it reaches infinity. The kinetic energy of the rocket is given by:
K=E−U
If the rocket is infinitely far from the Earth, then its potential energy is zero, and the kinetic energy is equal to E.
If the mechanical energy, E, is negative, it is not possible for the rocket to ever make it to infinity because its kinetic energy would have to be negative. In other words, if the mechanical energy is negative, then the object of mass m can never escape the gravitational pull of object M. We say that m is “gravitationally bound” to M.
If the mechanical energy, E, is exactly zero, then the object’s kinetic energy will become zero just as it reaches infinity. In other words, it will just barely be able to escape the gravitational pull from mass M. The condition for this to happen is:
E=0K=−U12mv2=GMmr∴vesc=√2GMr
which we can interpret as a condition for the speed of the rocket. If at some distance r from M, the rocket has the speed given by the condition above, then it will have enough kinetic energy to escape the gravitational pull of M. We call this speed the “escape velocity”.
Finally, if the mechanical energy is greater than zero, then the rocket will have enough energy to escape the gravitational pull of M and have a non-zero speed when it reaches infinity.
What is the escape velocity from the surface of the Earth?
- 4.29×106km/s
- 1.25×105km/s
- 11.2×km/s
- 9.81×km/s
- Answer
Show that an object of mass m in a circular orbit of radius r around a body of mass M has half of the kinetic energy required to escape the gravitational pull of M.
Solution
The only force acting on the object is gravity, so it has a mechanical energy given by:
E=U+KE=−GMmr+12mv2
In order for the object to just escape the gravitational pull of M, it’s mechanical energy must be equal to zero:
E=0∴Kesc=−U
Since the object is in a circular orbit, we can use Newton’s Second Law to find an expression for v2:
Fnet=mv2rGMmr2=mv2rGMr=v2
where in the second line we used the fact that Fnet is equal to the force of gravity exerted by M on the object. The kinetic energy of the object is thus:
K=12mv2K=12GMmr
You will notice that this is very similar to our expression for U. In fact, we have:
K=−12U∴K=12Kesc
Note:
We can also see that the velocity of an object in a circular orbit is equal to √GM/r, which is half the escape velocity, vesc=√2GM/r
Types of orbits
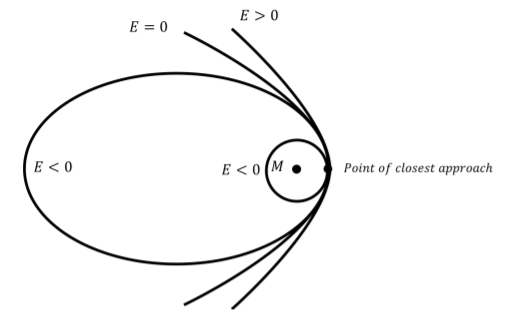
The mechanical energy of a body of mass m determines whether it is gravitationally bound to (i.e. cannot escape) the body of mass M. The path (orbit) that m will take depends on its velocity with respect to M. Clearly, if the velocity of m is directed at the center of M, then m will just collide with M. In all other cases, the orbit that m will take depends on the mechanical energy of m as well as the speed of m at the point of closest approach to M (see Figure 9.3.2). The velocity of m at the point of closest approach will always be perpendicular to the line joining the centers of m and M. The different possible orbits are:
- A circular orbit of radius R (where R is the distance of closest approach) if the mechanical energy is negative (i.e. it is bound) and the speed is exactly equal to the value necessary for the gravitational force to provide the required centripetal acceleration for uniform circular motion:
∑F=GMmR2=mv2R∴vcirc=√GMR
- An elliptical orbit if the mechanical energy is negative and the speed at the point of closest approach is different than that required for a circular orbit.
- A parabolic orbit if the mechanical energy is exactly zero.
- A hyperbolic orbit if the mechanical energy is bigger than zero.
The possible orbits are illustrated in Figure 9.3.2, and are curves in the family of “conic sections”, as they can be found by the intersection of a plane and a cone. All conic sections have at least one “focus” point (ellipses have two) that corresponds to the location of M.