13.1: The motion of a spring-mass system
- Page ID
- 19454
As an example of simple harmonic motion, we first consider the motion of a block of mass \(m\) that can slide without friction along a horizontal surface. The mass is attached to a spring with spring constant \(k\) which is attached to a wall on the other end. We introduce a one-dimensional coordinate system to describe the position of the mass, such that the \(x\) axis is co-linear with the motion, the origin is located where the spring is at rest, and the positive direction corresponds to the spring being extended. This “spring-mass system” is illustrated in Figure \(\PageIndex{1}\).
We assume that the force exerted by the spring on the mass is given by Hooke’s Law:
\[\begin{aligned} \vec F = -kx \hat x\end{aligned}\]
where \(x\) is the position of the mass. The only other forces exerted on the mass are its weight and the normal force from the horizontal surface, which are equal in magnitude and opposite in direction. Therefore, the net force on the mass is the force from the spring.
As we saw in Section 8.4, if the spring is compressed (or extended) by a distance \(A\) relative to the rest position, and the mass is then released, the mass will oscillate back and forth between \(x=\pm A\)1, which is illustrated in Figure \(\PageIndex{1}\). We call \(A\) the “amplitude of the motion”. When the mass is at \(x=\pm A\), its speed is zero, as these points correspond to the location where the mass “turns around”.
Description using energy
We can describe the motion of the mass using energy, since the mechanical energy of the mass is conserved. At any position, \(x\), the mechanical energy, \(E\), of the mass will have a term from the potential energy, \(U\), associated with the spring force, and kinetic energy, \(K\):
\[\begin{aligned} E = U + K =\frac{1}{2}kx^2 + \frac{1}{2}mv^2\end{aligned}\]
We can find the mechanical energy, \(E\), by evaluating the energy at one of the turning points. At these points, the kinetic energy of the mass is zero, so \(E=U(x=A)=1/2kA^2\). We can then write the expression for mechanical energy as:
\[\frac{1}{2}kx^{2}+\frac{1}{2}mv^{2}=\frac{1}{2}kA^{2}\]
We can thus always know the speed, \(v\), of the mass at any position, \(x\), if we know the amplitude \(A\):
\[\begin{aligned} v(x) = \sqrt{\frac{k(A^{2}-x^{2})}{m}}\end{aligned}\]
If you double the amplitude of the motion of a mass attached to a spring, its maximum speed will be:
- double.
- \(\sqrt 2\) times greater.
- the same.
- halved.
- Answer
Kinematics of simple harmonic motion
We can use Newton’s Second Law to obtain the position, \(x(t)\), velocity, \(v(t)\), and acceleration, \(a(t)\), of the mass as a function of time. The \(x\) component of Newton’s Second Law for the mass attached to the spring can be written:
\[\begin{aligned} \sum F_x = -kx = ma\end{aligned}\]
We can write the acceleration in Newton’s Second Law more explicitly as the second derivative of the position, \(x(t)\), with respect to time. If we do this, we can see that Newton’s Second Law for the mass attached to the spring is a differential equation for the function \(x(t)\) (we call it an “equation of motion”):
\[\begin{aligned} ma&=-kx \\[4pt] m\frac{d^{2}x}{dt^{2}}&=-kx \end{aligned}\]
\[\therefore \frac{d^{2}x}{dt^{2}}=-\frac{k}{m}x\]
We want to find the position function, \(x(t)\). Equation 13.1.2 tells us that the second derivative of \(x(t)\) with respect to time must equal the negative of the \(x(t)\) function multiplied by a constant, \(k/m\). Without having taken a course on differential equations, it might not be obvious what the function \(x(t)\) could be. Several, equivalent functions can satisfy this equation. One possible choice, which we present here as a guess, is2:
\[x(t)=A\cos(\omega t+\phi)\]
where \(A\), \(\omega\), and \(\phi\) are constants that we need to determine. We can take the second order derivative with respect to time of the function above to verify that it indeed “solves” the differential equation:
\[\begin{aligned} x(t) &= A \cos(\omega t + \phi)\\[4pt] \frac{d}{dt}x(t) &= -A\omega\sin(\omega t + \phi)\\[4pt] \frac{d^2}{dt^2}x(t) &=\frac{d}{dt}\left( -A\omega\sin(\omega t + \phi)\right)= -A\omega^2\cos(\omega t + \phi)\\[4pt] \therefore \frac{d^2}{dt^2}x(t) &= - \omega^2 x(t)\end{aligned}\]
The last equation has exactly the same form as Equation 13.1.2, which we obtained from Newton’s Second Law, if we define \(\omega\) as:
\[\omega = \sqrt{\frac{k}{m}}\]
We call \(\omega\) the “angular frequency” of the spring-mass system. We have found that our guess for \(x(t)\) satisfies the differential equation.
What is the SI unit for angular frequency?
- \(\text{Hz}\)
- \(\text{rad/s}\)
- \(\text{N}^{1/2}\text{m}^{-1/2}\text{kg}^{-1/2}\)
- All of the above
- Answer
-
All of the above
In Chapter3, we found, \(x(t)\), from a function, \(a(t\)), by using simple integration. You may be wondering why we can’t do the same thing in order to find \(x(t)\) for the mass-spring system. The difference is that, before, the acceleration was a function of time. Here, the acceleration is a function of \(x\). This means that we have to use a different method to solve for \(x(t)\), which is why we are making these “guesses” to solve a differential equation.
We still need to identify what the constants \(A\) and \(\phi\) have to do with the motion of the mass. The constant \(A\) is the maximal value that \(x(t)\) can take (when the cosine is equal to 1). This corresponds to the amplitude of the motion of the mass, which we already had labeled, \(A\). The constant, \(\phi\), is called the “phase” and depends on when we choose \(t=0\) to be. Suppose that we define time \(t=0\) to be when the mass is at \(x=A\); in that case:
\[\begin{aligned} x(t=0) &= A\\[4pt] A \cos(\omega t + \phi) &= A\\[4pt] A \cos(\omega (0) + \phi) &= A\\[4pt] \cos(\phi) &= 1\\[4pt] \therefore \phi = 0\end{aligned}\]
If we define \(t=0\) to be when the mass is at \(x=A\), then the phase, \(\phi\), is zero. In general, the value of \(\phi\) can take any value between \(-\pi\) and \(+\pi\)3 and, physically, corresponds to our choice of when \(t=0\) (i.e. the position of the mass when we choose \(t=0\)).
Since we have determined the position as a function of time for the mass, its velocity and acceleration as a function of time are easily found by taking the corresponding time derivatives:
\[\begin{aligned} x(t) &= A \cos(\omega t + \phi)\\[4pt] v(t) &= \frac{d}{dt}x(t) = -A\omega\sin(\omega t + \phi)\\[4pt] a(t)&= \frac{d}{dt}v(t) = -A\omega^2\cos(\omega t + \phi)\end{aligned}\]
What is the value of \(\phi\) if we choose \(t=0\) to be when the mass is at \(x=0\) and moving in the positive \(x\) direction?
- \(\pi\)
- \(-\pi\)
- \(\pi/2\)
- \(-\pi/2\)
- Answer
The position of the mass is described by a sinusoidal function of time; we call this type of motion “simple harmonic motion”. The position and velocity as a function of time for a spring-mass system with \(m=1\text{kg}\), \(k=4\text{N/m}\), \(A=10\text{m}\) are shown in Figure \(\PageIndex{2}\) for two different choices of the phase, \(\phi=0\) and \(\phi=\pi/2\).
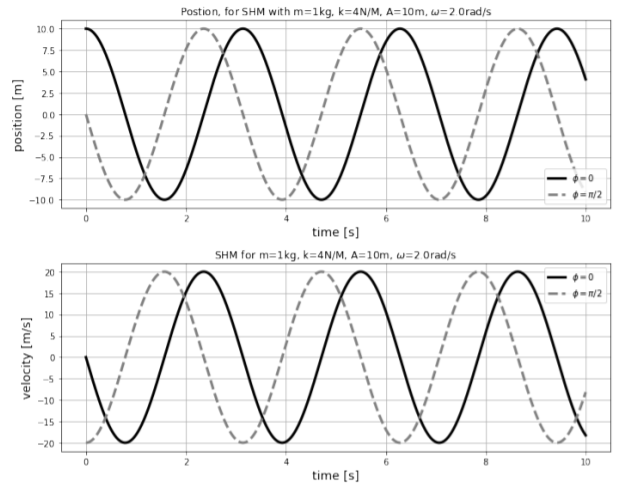
We can make a few observations about the position and velocity illustrated in Figure \(\PageIndex{2}\):
- Changing the phase, \(\phi\), results in an horizontal shift of the functions. A positive phase results in a shift of the functions to the left.
- The highest speed corresponds to a position of \(x=0\) and the largest position, \(x=\pm A\), corresponds to a speed of zero.
- \(\phi = 0\) corresponds to the “initial condition” at \(t=0\), where the position of the mass is \(x=A\) and its speed is \(v=0\).
- \(\phi = \pi/2\) corresponds to the “initial condition” at \(t=0\), where the position of the mass is \(x=0\) and its velocity is in the negative direction, and with maximal amplitude.
- The position is always between \(x=\pm A\), and the velocity is always between \(v=\pm A\omega\).
The motion of the spring is clearly periodic. If the period of the motion is \(T\), then the position of the mass at time \(t\) will be the same as its position at \(t+T\). The period of the motion, \(T\), is easily found:
\[T=\frac{2\pi}{\omega}=2\pi\sqrt{\frac{m}{k}}\]
And the corresponding frequency is given by:
\[f=\frac{1}{T}=\frac{\omega}{2\pi}=\frac{1}{2\pi}\sqrt{\frac{k}{m}}\]
It should now be clear why \(\omega\) is called the angular frequency, since it is related to the frequency of the motion.
In order to double the oscillation period of a spring-mass system, you can
- double the ratio of the mass over the spring constant.
- quadruple the mass.
- halve the spring constant.
- All of the above.
- Answer
Analogy with uniform circular motion
We can make an analogy between the mathematical description of the motion of a spring-mass system and that of uniform circular motion. Consider a particle that is moving along a circle of radius \(A\), with constant angular speed \(\omega\), as illustrated in Figure \(\PageIndex{3}\).
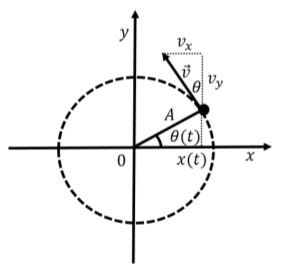
The angular position, \(\theta(t)\), of the particle is given by:
\[\begin{aligned} \theta(t) = \theta_0 + \omega t\end{aligned}\]
if the particle was located at an angular position \(\theta_0\) at \(t=0\) (\(\theta_0=0\) in Figure \(\PageIndex{3}\)). The \(x\) coordinate of the particle is given by:
\[\begin{aligned} x(t) = A\cos(\theta(t)) = A\cos(\theta_0 + \omega t)\end{aligned}\]
We can see that the \(x\) coordinate of the particle has the same functional form as the position for simple harmonic motion. The same is true for the particle’s velocity. The magnitude of the particle’s velocity is given by:
\[\begin{aligned} v = \omega r = \omega A\end{aligned}\]
where \(r=A\) is the radius of the circle. The \(x\) component of the particle’s velocity is easily found from the figure and is given by:
\[\begin{aligned} v_x(t) = -v\sin(\theta(t)) = -\omega A\sin(\theta_0 + \omega t)\end{aligned}\]
We can visualize simple harmonic motion as if it were the projection onto the \(x\) axis of uniform circular motion with angular speed \(\omega\) about a circle with radius \(A\). The phase \(\phi\) corresponds to the angular position of the particle around the circle, \(\theta_0\), at time \(t=0\). When the particle crosses the \(y\) axis (\(x=0\)), its velocity is in the \(x\) direction, so the \(x\) component of the velocity is maximal. When the particle crosses the \(x\) axis (\(x=\pm A\)), the \(x\) component of the velocity is zero.
Here’s a visualization of uniform circular motion projected onto the \(x\) axis:
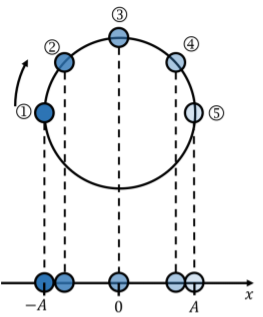
Figure \(\PageIndex{4}\) shows a ball moving at a constant speed around a circle of radius \(A\). In this diagram, I have taken snapshots of the ball’s motion at regular time intervals as the ball moves from Position 1 to Position 5. Since the speed is constant, the balls are evenly spaced out around the circle. At the bottom of the figure, you can see what it would look like if we only considered the motion in the \(x\) direction (this is the projection of the motion onto the \(x\) axis). You could also think of this as what the motion would look like if you looked up at the circle from below. As you can see, this projection looks a lot like the motion of a mass on a spring. The motion of the ball is constrained between \(-A\) and \(+A\) (the turning points), and the velocity of the ball, in the \(x\) direction, will be highest when \(x=0\). There are tons of videos online that show animations of this concept, just look up “SHM as a projection of circular motion” and you will get lots of different ways to visualize this.
Footnotes
1. As long as there is no friction to reduce the mechanical energy of the mass.
2. Other possible guesses that work are \(A \sin(\omega t + \phi)\), and \(x(t) = A\cos(\omega t) + B\sin(\omega t)\).
3. The argument to the cosine function is in radians, since the angular frequency is usually defined in radians per second. The value of \(\phi\) is constrained to be within that range, since the cosine function is periodic with a period \(2\pi\).