17.3: Charges in a Conductor
( \newcommand{\kernel}{\mathrm{null}\,}\)
We can use Gauss’ Law to understand how charges arrange themselves on a conductor. Consider (again) an infinite plane that carries a total charge per unit area, σ, similar to what we considered in Example 17.2.3. In this case, we explicitly consider the plane to be a conductor and to have a finite thickness. If we zoom into the plane, we can illustrate that the charges are located on the surface of the plane, as illustrated in Figure 17.3.1, where the plane is seen edge on. Thus, the charge density at the surface is half of the total charge density of the plane.
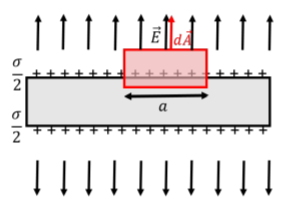
To determine the electric field near the plane, we choose a gaussian surface that is a box (as in Example 17.2.3), but require the lower end of the box to go through the plane, as illustrated in Figure 17.3.1. With this choice of gaussian surface, only the top surface (area a2) will have flux through it, since the electric field inside a conductor must be zero1. The total flux is given by:
∮→E⋅d→A=∫topEdA=Ea2
The charge enclosed is given by:
Qenc=σ2a2
where we used the fact that only half of the charges are inside the volume enclosed by our gaussian surface, so that the charge per unit area is half (σ2) of that for the entire plane. Applying Gauss’ Law, we find that the electric field is given by:
∮→E⋅d→A=Qencϵ0Ea2=σa22ϵ0∴E=σ2ϵ0(Field above an infinite plane)
as before, but the factor of 2 now came from the charge density, rather than from the fact that two of the faces of the box had non-zero flux (as was the case in Example 17.2.3). We can generalize this result to determine the electric field near the surface of any conductor. Very close to the surface of any object, one can consider the surface as being similar to an infinite plane. If that surface carries charge per unit area, σ, then the electric field just above the surface is given by:
E=σϵ0(Field near a conducting surface)
In this case, there is no factor of 2, because the charge density in this equation is the charge density of the conductor (not the charge density one side of the surface). In the previous equation, the charge density on the surface of the conducing plane was σ2.
Consider, now, a neutral spherical conducting shell, as shown from the side in the left panel of Figure 17.3.2. When a charge, +Q, is placed at the center of the shell (right panel), charges inside the shell will move until the field inside the conducting material of the shell is identically zero. The negative charges will move towards the inner surface (as they are attracted to +Q) and positive charges will be repelled onto the outer surface, under the influence of the electric field created by +Q (shown in the diagram as →EQ). Eventually, the separation of charges will lead to an electric field (shown in the diagram as →Eσ) in the opposite direction. The charges will stop moving once the total electric field in the conductor is zero (when the two fields cancel exactly everywhere in the conductor).
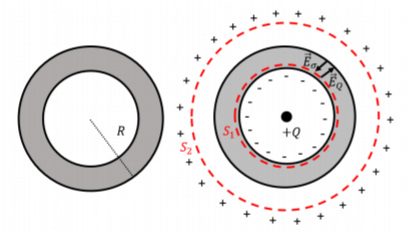
We can use Gauss’ Law to determine the amount of charge that has accumulated on the inner surface. Consider the gaussian spherical surface, S1, in Figure 17.3.2, that is concentric with the shell and has a radius such that the surface is just inside the shell. Since the electric field is zero inside the shell, the flux out of the gaussian surface must be zero. By Gauss’ Law, the amount of charge enclosed by the surface must also be zero. Thus, a total charge, −Q, will have accumulated on the inner surface of the conductor (since Qenc=−Q+Q=0). Because one cannot just create charge from nothing, there must be an equal amount of opposite charge, +Q, on the outer surface of the shell. This is true of any conducting material with a cavity inside of it: if you place a charge +Q in the cavity, a charge, −Q will accumulated on the inner surface and a charge, +Q, will accumulate on the outer surface.
If we now consider the flux out of the surface, S2, outside of the shell, the net charge enclosed will be Qenc=+Q−Q+Q=+Q. The flux out of the spherical surface of radius, say, r, is then given by:
∮→E⋅d→A=E(4πr2)
and the electric field, from Gauss’ Law, is simply that of a point charge, +Q:
E=14πϵ0Qr2
and the shell has no effect on the field in regions where there is no conducting material from the shell. Right at the surface of the shell (outer radius, R), the surface charge density is given by:
σ=Q4πr2
Above, we found the electric field at the surface of a conductor that carries charge per unit area, σ, to be:
E=σϵ0
which is clearly the same result that we obtained using the spherical surface, S2:
E=σϵ0=14πϵ0Qr2
Note that we found the electric field using Gauss’ Law only in this last case, and found it to be equal to the electric field that one obtains from Coulomb’s law. Thus, Gauss’ Law only works if the field has an “inverse square law” dependence. If Gauss’ Law does not provide the correct electric field, then the force does not depend on 1/r2. Gauss’ Law can be used to make extremely stringent tests of whether the force goes as 1/r2 or deviates from this model.
Footnotes
1. Since charges can freely move in a conductor, they will move until there is no reason to move. Eventually, the charges accumulate in such a way that the net field in the conductor is zero. For a plane, this means that half of the charges will move to each side, as illustrated.

