19.3: Ohm’s Law
( \newcommand{\kernel}{\mathrm{null}\,}\)
In the previous section, we developed a microscopic model of charges moving in a conductor, but did not describe how this motion is affected by the electric field in the conductor (or equivalently, the potential difference across the conductor). “Ohm’s Law” states that the current density, →j, at some position in the conductor is proportional to the electric field, →E, at that same position in the conductor:
→j∝→E
→j=σ→E
where we have introduced the “conductivity”, σ, as the constant of proportionality. Conductivity is a property of the material from which the conductor is made, and is a measure of how large a current density (and by extension, current) there will be in material given a certain electric field. Materials with a high conductivity are said to be good conductors, as a large current will result from a small electric field. Gold and copper are examples of materials with a high conductivity.
What is the conductivity of an ideal insulator?
- 0.
- Roughly 1.
- Infinite.
- Answer
-
Resistivity
For convenience, one often describes how well a material conducts charges using the “resistivity”, ρ, which is simply defined as the inverse of conductivity:
ρ=1σ
Materials with a high resistivity are poor conductors; they tend to “resist” the formation of a current when an electric field is applied. Insulators have high resistivity.
The resistivity of most (but not all) materials has been observed to increase linearly with the temperature of the material. One can picture that, as atoms in the material vibrate more, it is more difficult for electrons to conduct through the material as they will interact with more atoms. The resistivity, ρ, at a certain temperature, T, is usually modeled as follows:
ρ(T)=ρ0[1+α(T−T0)]
where, ρ0, is a “reference resistivity” measured at a “reference temperature”, T0 (usually \SI20\degreeC). α is the “temperature coefficient” of the material. The temperature dependence of the resistivity is illustrated in Figure 19.3.1.
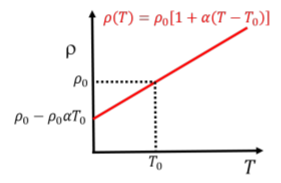
This “linear model” (since resistivity increases linearly with temperature) is empirically found to be valid for many materials over a large range of temperatures, although it is not expected to hold at extreme temperatures (either very low or very high). Furthermore, for semi-conducting materials (such as silicon and germanium), resistivity is found to decrease as a function of temperature.
What is the slope of the resistivity vs temperature as shown in Figure 19.3.1?
- α.
- ρ0αT.
- ρ0T.
- ρ0α.
- Answer
Table 19.3.1 shows a list of common materials and their conductivity, resistivity, and temperature coefficients (defined at a reference temperature T0=20∘C).
| Material | Resistivity [Ω⋅m] | Temperature coefficient [∘C−1] | Free electron density [m−3] |
|---|---|---|---|
| Silver | 1.59×10−8 | 0.0038 | 5.86×1028 |
| Copper | 1.68×10−8 | 0.0040 | 8.46×1028 |
| Gold | 2.44×10−8 | 0.0034 | 5.90×1028 |
| Aluminum | 2.74×10−8 | 0.0039 | 18.1×1028 |
| Iron | 9.70×10−8 | 0.0050 | 17.0×1028 |
| Silicon | 0.1−1000 | −0.0750 | 0 |
| Rubber | (1−100)×1013 | 0 | 0 |
| Quartz | 7.5×1017 | 0 | 0 |
Table 19.3.1: Resistivity, free electron density and temperature coefficients of common materials. All properties are listed for a reference temperature of 20∘C.

