22.4: Solenoids and Toroids
- Page ID
- 19536
In order to create strong magnetic fields, the most practical method is to combine many loops of current together into a “solenoid” (a coil). Electromagnets function on this principle and are ubiquitous in our lives. Figure \(\PageIndex{1}\) shows the magnetic field from a single loop of current.
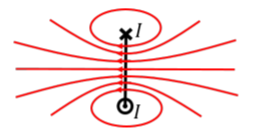
When several loops of current are brought close together, as in Figure \(\PageIndex{2}\), the magnetic field inside the solenoid becomes uniform, and the magnetic field just outside the solenoid approaches zero.
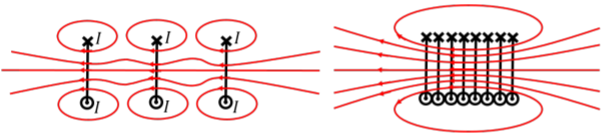
We can use Ampere’s Law to determine the strength of the magnetic field inside of a solenoid, under the assumption that the magnetic field is uniform in the volume of the solenoid and zero just outside. Consider a solenoid with current, \(I\), going through it, that contains \(n\) loops per unit length. In order to determine the magnetic field, \(B\), inside of the solenoid, consider the rectangular Amperian loop, abcd, of length, \(l\), illustrated in Figure \(\PageIndex{3}\).
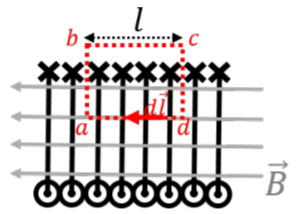
In order to evaluate the circulation of the magnetic field around the loop, abcd, we divide the loop up into segments, and evaluate the path integral (\(\int\vec B\cdot d\vec l\)) over each segment, then add those together to obtain the integral over the closed path:
\[\begin{aligned} \oint_{abcd} \vec{B}\cdot d\vec l=\int_{a}^{b}\vec B\cdot d\vec l+\int_{b}^{c}\vec B\cdot d\vec l+\int_{c}^{d}\vec B\cdot d\vec l+\int_{d}^{a}\vec B\cdot d\vec l \end{aligned}\]
Over each segment, the vector \(d \vec l\) will be parallel to that segment. Only the last term is non-zero. The integrals over the segments \(ab\) and \(cd\) are zero because the magnetic field is perpendicular to \(d \vec l\) over those segments (so the scalar product is zero). The integral over the segment \(bc\) is zero because the magnetic field is zero just outside the solenoid. The integral over the last segment, where \(d \vec l\) and \(\vec B\) are parallel, is simply given by:
\[\begin{aligned} \oint_{abcd}\vec B\cdot d\vec l=\int_{d}^{a}\vec B\cdot d\vec l=B\int_{d}^{a}dl=Bl \end{aligned}\]
since the length of the segment is \(l\), and the magnetic field is constant in magnitude.
In order to apply Ampere’s Law, we must determine the current that is enclosed by our Amperian loop. Since the rectangular loop has a length, \(l\), it will enclose \(N = nl\) loops of current, \(I\), since there are \(n\) loops per unit length. Thus the enclosed current is \(I^{enc} = nlI\). Applying Ampere’s Law, we find the magnetic field inside a solenoid:
\[\begin{aligned} \oint \vec B\cdot d\vec l&=\mu_{0}I^{enc} \\ Bl&=\mu_{0}nIl \end{aligned}\]
\[\therefore B=\mu_{0}nI\quad\text{(Field inside a solenoid)}\]
which does not depend on our (arbitrary) choice of making an Amperian loop with an arbitrary length of \(l\). In practice, when solenoids are used as electromagnets, they are typically filled with a ferromagnetic material, which will magnetize when there is a current, resulting in a stronger magnetic field. This is usually done by winding a wire around an iron rod.
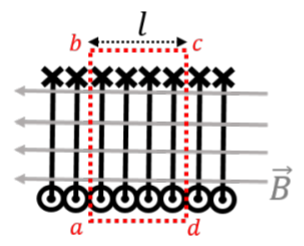
Note that if we extend the Amperian loop so that the bottom segment is also outside the solenoid, as in Figure \(\PageIndex{4}\), it is easy to show that the magnetic field immediately outside of the solenoid must be zero. Indeed, in this case, there are an equal number of currents coming out of the page as there are going into the page, so that the net current that is enclosed by the Amperian loop (the net current that crosses the plane of the loop) is identically zero, so that the circulation must be zero, implying that the magnetic field is zero just outside the solenoid.
A toroid can be thought of as a solenoid that has been bent into the shape of a circle (or rather, a torus), as illustrated in Figure \(\PageIndex{5}\). Inside the toroid, the magnetic field forms concentric circles (not shown).
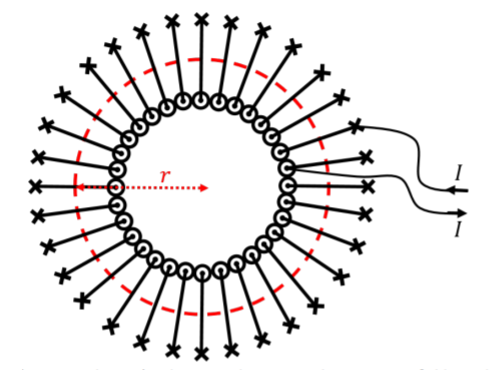
Again, we can use Ampere’s Law to determine the strength of the magnetic field inside the toroid. Consider the circular Amperian loop of radius \(r\) that is illustrated in Figure \(\PageIndex{5}\). Since the magnetic field is parallel to the Amperial loop everywhere along the loop, and the magnetic field does not change magnitude (by symmetry), the circulation is given by:
\[\begin{aligned} \oint\vec B\cdot d\vec l=B(2\pi r) \end{aligned}\]
If the toroid contains \(N\) loops of current, then the enclosed current is given by \(I^{enc} = NI\), since the Amperian loop include \(N\) times the current \(I\) coming out of the page. Ampere’s Law thus gives the magnitude of the magnetic field as:
\[\begin{aligned} \oint\vec B\cdot d\vec l&=\mu_{0}I^{enc} \\ B(2\pi r)&=\mu_{0}NI \\ \therefore B&=\frac{\mu_{0}NI}{2\pi r} \end{aligned}\]
which decreases in magnitude with increasing radius, as long as we are inside the toroid. It is easy to show, by using Amperian loops that are either smaller or bigger than the toroid, that the magnetic field everywhere outside of the toroid is exactly zero (as those Amperian loops will enclose no net current). In a toroid, the magnetic field lines form closed circles. For a solenoid, there must exist a magnetic field somewhere outside the solenoid, in order for the field lines inside the solenoid to close. We can usually ignore these if the solenoid is long, as the field outside will be very weak, and very close to zero very close the solenoid (as we showed with Amp`ere’s Law above).
In Figure \(\PageIndex{5}\), the magnetic field makes concentric circles. What direction do the field lines point?:
- Clockwise.
- Counter clockwise.
- Upwards.
- Not enough information to tell.
- Answer

