23.4: The induced electric field and eddy currents
( \newcommand{\kernel}{\mathrm{null}\,}\)
So far, we have described electromagnetic induction in terms of the voltage that is induced by a changing magnetic field. This voltage is related to an electric field, which we discuss in this section. In Faraday’s Law, the voltage is induced across a closed loop (and can be thought of as an ideal battery placed in the loop). This is illustrated in Figure 23.4.1 which shows a loop in the plane of the page, and a magnetic field out of the plane of the page.
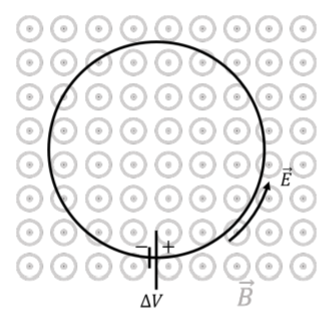
In Figure 23.4.1, with the induced voltage as shown, is the magnetic field increasing or decreasing?
- The magnetic field is increasing.
- The magnetic field is decreasing.
- Answer
-
As you recall, the electric potential difference between two points, A and B, is obtained from the electric field:
ΔV=∫BA→E⋅d→l
In the case of an induced voltage across a loop, the points A and B are the same. The integral is thus over a closed path:
ΔV=∮→E⋅d→l
We can include this into Faraday’s Law by using the electric field instead of the potential difference:
ΔV=−dΦBdt
∴∮→E⋅d→l=−dΦBdt
where the last line is a more general form of Faraday’s Law. Note that in the case of electrostatics, where the electric field is produced by a distribution of charges, the integral ∮→E⋅d→l must be zero, since the electric force is conservative; the work done by the electric field on a charge q over a closed path, which is just a charge q multiplied by that integral, must be zero. The force from an electric field that is induced by a time-varying magnetic field is not conservative!
Faraday’s Law as expressed with the electric field is much more general, and implies that a time-varying magnetic field will induce an electric field. This is true, independently of there existing a physical wire to carry the induced current.
A circular region with radius, R, of space contains a magnetic field that is uniform, and decreasing in magnitude with time:
→B(t)=B0(1−at)ˆz
where a and B0 are positive constants. Determine the electric field at a distance, r, from the center of the region, inside and outside of the region with the magnetic field.
Solution
Figure 23.4.2 shows the circular region of magnetic field, as well as a circular path of radius, r, that defines the region over which we calculate the flux of the magnetic field.
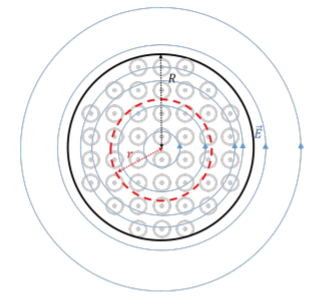
First, we consider the induced electric field in the region with a magnetic field, where r<R. We choose a circle of radius r to calculate the flux of the magnetic field. Since the magnetic field is uniform within that region, the flux is given by:
ΦB=→B⋅→A=BA=B0(1−at)πr2
The circulation of the electric field is easily found, since the electric field forms concentric circles (by symmetry):
∮→E⋅d→l=∮Edl=E∮dl=E(2πr)
Applying Faraday’s Law, the electric field is found to be:
∮→E⋅d→l=−dΦBdtE(2πr)=−ddtB0(1−at)πr22E=B0ar∴E=B0a2r(inside the region of magnetic field)
and we see that, inside the region with the magnetic field, the strength of the induced electric field is proportional to the distance from the center of the region (i.e. it increases linearly with r).
For the region where the magnetic field is zero, we again calculate the circulation of the electric field around a circular loop of radius r>R:
∮→E⋅d→l=∮Edl=E∮dl=E(2πr)
The flux of the magnetic field through that loop is however related to the area of the region with the magnetic field (of radius, R):
ΦB=→B⋅→A=BA=B0(1−at)πR2
Again, applying Faraday’s Law:
∮→E⋅d→l=−dΦBdtE(2πr)=−ddtB0(1−at)πR22Er=B0aR2∴E=B0aR22r(outside the region of magnetic field)
Outside the region with a magnetic field, the magnitude of the electric field decreases with the distance from the center of the region.
Discussion
In this example, we determined the electric field that is induced by a varying magnetic field. In this case, the electric field lines form closed circles and result in a non-conservative force. When the electric field is formed by a distribution of electric charges, the field lines begin and end on charges, which is not the case for an induced electric field.
Magnetic braking
When a conducting material moves into a region of magnetic field, an electric field forming closed loops is induced in the material, thus inducing small current loops, called “eddy currents”. The magnetic field can then exert a force on those currents, effectively resulting in a force on the material. This is the principle behind magnetic braking, which is used in some trains and in other applications.
Figure 23.4.3 illustrates how a magnetic brake can be used to slow a rotating wheel made of a conducting material (the material must conduct or the induced electric field will not produce any current). A magnetic field is produced (e.g. by a fixed permanent magnet) in a direction perpendicular to the wheel, over a small area (shown at the bottom of the wheel in Figure 23.4.3).
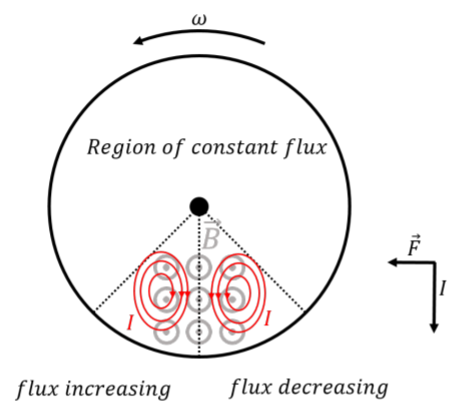
For material located at the bottom left of the wheel, the magnetic flux is increasing, since the material is moving from a region with no magnetic field into a region with a magnetic field. In that part of the region, clockwise eddy currents will form, as those result in a magnetic field into the page, to counter the increasing magnetic flux (Lenz’s Law). The bottom right side of the wheel is leaving the magnetic field, and will thus have eddy currents in the opposite direction. The currents from both sides add up in the center, resulting in a net downwards current. The magnetic force on that downwards current is to the left, resulting in a torque that slows the wheel. This is magnetic braking.
Again, this is no more than conservation of energy at play. Since we induce currents by making the wheel move into/out of a region of magnetic field, the electrical energy in those currents must come from somewhere (either we do work to keep the wheel rotating, or the wheel loses kinetic energy). Any time that we try to move a conductor through a magnetic field, in a way that current is induced, we will have to exert a force and do work. In the case of magnetic braking, the wheel will convert its rotational kinetic energy into heat (the eddy currents will heat up the wheel). The main issue with magnetic braking is that one needs to be able to dissipate the heat. The main advantage is that there are no parts that wear out, as opposed to braking with friction. In addition, magnetic braking is very smooth, and only acts when there is motion. As soon as the wheel stops rotating, the magnetic flux is constant everywhere and the eddy currents disappear.
Suppose that the magnetic field in Figure 23.4.3 pointed into the page. Would the magnetic break still work?
- Yes.
- No.
- Answer

