03. Analysis Tools 2
( \newcommand{\kernel}{\mathrm{null}\,}\)
Force and Motion
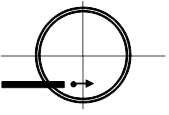
Protons are injected at 2.0 x 105 m/s into a 2000 turn-per-meter solenoid carrying 3.0 A clockwise in the diagram at right. Determine the protons' orbit radius.
A solenoid is a very useful device for generating a uniform magnetic field. A solenoid consists of a wire carrying current i wrapped N times around a hollow core of radius R and length L. Typically, L is substantially larger than R (much larger than illustrated below). Contrast this with a coil of wire, in which R is typically larger than L.
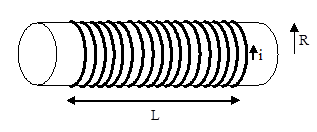
In a solenoid, the magnetic field inside the core is extremely uniform. In a sense, the small radius and long length "concentrate" the magnetic field within the core leading to an approximately constant value. Again, this contrasts with a coil of wire, in which the field varies at different locatoins inside and outside the coil.
By using Ampere's Law, and a few simplifying approximations, it can be shown that the field inside the solenoid is given by:
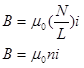
where n is the turn density, the number of loops of wire, or turns, per meter. Therefore, the solenoid described in the problem creates a magnetic field
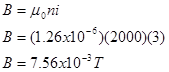
This field is directed into the page since the current flows clockwise.
This magnetic field will create a magnetic force on the proton. When the proton first enters the device the magnetic force will be directed upward, causing the path of the proton to bend upward. As the proton begins to move upward the direction of the magnetic force changes, and when the proton is moving directly upward the force will be to the left. This will cause the proton to bend toward the left. When the proton is moving directly leftward the magnetic force will be directed downward, causing the proton to begin to bend downward. And so on...
Since the magnetic force is always perpendicular to the direction of travel of the proton, the magnetic force causes the proton to make a non-stop left-hand turn! The proton will begin moving in circles due to this force, and since the force has no component along the direction of travel of the proton it does no work on the proton and the proton moves at constant speed. Basically, magnetic fields "steer" charged particles but don't make them speed up or slow down.
With this in mind, let's apply Newton's Second Law to the proton the instant it enters the solenoid:
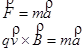
It enters the solenoid traveling in the +x-direction, and it will accelerate toward the center of its circular path, the +y-direction. (Remember that this radial acceleration can be expressed as v2/r.)
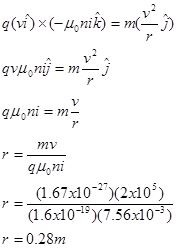
The proton will circle at constant speed at this radius.


