5.6: The Lorentz Transformation
- Page ID
- 4517
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Describe the Galilean transformation of classical mechanics, relating the position, time, velocities, and accelerations measured in different inertial frames
- Derive the corresponding Lorentz transformation equations, which, in contrast to the Galilean transformation, are consistent with special relativity
- Explain the Lorentz transformation and many of the features of relativity in terms of four-dimensional space-time
We have used the postulates of relativity to examine, in particular examples, how observers in different frames of reference measure different values for lengths and the time intervals. We can gain further insight into how the postulates of relativity change the Newtonian view of time and space by examining the transformation equations that give the space and time coordinates of events in one inertial reference frame in terms of those in another. We first examine how position and time coordinates transform between inertial frames according to the view in Newtonian physics. Then we examine how this has to be changed to agree with the postulates of relativity. Finally, we examine the resulting Lorentz transformation equations and some of their consequences in terms of four-dimensional space-time diagrams, to support the view that the consequences of special relativity result from the properties of time and space itself, rather than electromagnetism.
The Galilean Transformation Equations
An event is specified by its location and time \((x, y, z, t)\) relative to one particular inertial frame of reference \(S\). As an example, \((x, y, z, t)\) could denote the position of a particle at time \(t\), and we could be looking at these positions for many different times to follow the motion of the particle. Suppose a second frame of reference \(S'\) moves with velocity \(v\) with respect to the first. For simplicity, assume this relative velocity is along the x-axis. The relation between the time and coordinates in the two frames of reference is then
\[\begin{align} x &= x' + vt \label{eq1} \\[4pt] y &= y' \label{eq2} \\[4pt] x &= z'. \label{eq3} \end{align} \]
Implicit in these equations is the assumption that time measurements made by observers in both \(S\) and \(S'\) are the same. That is,
\[t = t' \label{eq4} \]
Equations \ref{eq1}-\ref{eq4} are known collectively as the Galilean transformation.
We can obtain the Galilean velocity and acceleration transformation equations by differentiating these equations with respect to time. We use \(u\) for the velocity of a particle throughout this chapter to distinguish it from \(v\), the relative velocity of two reference frames. Note that, for the Galilean transformation, the increment of time used in differentiating to calculate the particle velocity is the same in both frames, \(dt = dt'\). Differentiation yields
\[u_x = u'_x + v, \,u_y = u'_y, \,u_z = u'_z \nonumber \]
and
\[a_x = a'_x, \,a_y = a'_y, \,a_z = a'_z. \nonumber \]
We denote the velocity of the particle by \(u\) rather than \(v\) to avoid confusion with the velocity \(v\) of one frame of reference with respect to the other. Velocities in each frame differ by the velocity that one frame has as seen from the other frame. Observers in both frames of reference measure the same value of the acceleration. Because the mass is unchanged by the transformation, and distances between points are uncharged, observers in both frames see the same forces \(F = ma\) acting between objects and the same form of Newton’s second and third laws in all inertial frames. The laws of mechanics are consistent with the first postulate of relativity.
The Lorentz Transformation Equations
The Galilean transformation nevertheless violates Einstein’s postulates, because the velocity equations state that a pulse of light moving with speed \(c\) along the x-axis would travel at speed \(c - v\) in the other inertial frame. Specifically, the spherical pulse has radius \(r = ct\) at time \(t\) in the unprimed frame, and also has radius \(r' = ct'\) at time t' in the primed frame. Expressing these relations in Cartesian coordinates gives
\[ \begin{align} x^2 + y^2 + z^2 - c^2t^2 &= 0 \label{eq21} \\[4pt] x'^2 + y'^2 + z'^2 - c^2t'^2 &= 0. \label{eq22} \end{align} \]
The left-hand sides Equations \ref{eq21} and \ref{eq22} can be set equal because both are zero. Because \(y = y'\) and \(z = z'\), we obtain
\[x^2 - c^2t^2 = x'^2 - c^2t'^2. \nonumber \]
This cannot be satisfied for nonzero relative velocity \(v\) of the two frames if we assume the Galilean transformation results in \(t = t'\) with \(x = x' + vt'\).
To find the correct set of transformation equations, assume the two coordinate systems \(S\) and \(S'\) in Figure \(\PageIndex{1}\). First suppose that an event occurs at \((x', 0, 0, t')\) in \(S'\) and at \((x, 0, 0, t)\) in \(S\), as depicted in Figure \(\PageIndex{1}\).
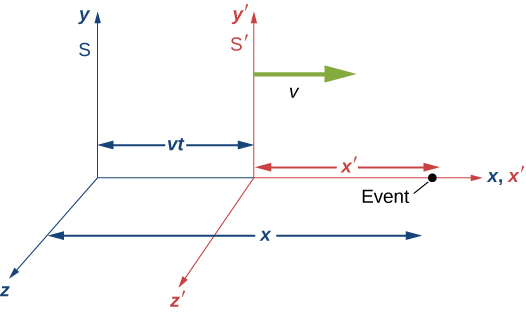
Suppose that at the instant that the origins of the coordinate systems in S and S' coincide, a flash bulb emits a spherically spreading pulse of light starting from the origin. At time t, an observer in S finds the origin of S' to be at \(x = vt\). With the help of a friend in S, the S' observer also measures the distance from the event to the origin of S' and finds it to be \(x'\sqrt{1 - v^2/c^2}\). This follows because we have already shown the postulates of relativity to imply length contraction. Thus the position of the event in S is
\[x = vt + x'\sqrt{1 - v^2/c^2} \nonumber \]
and
\[x' = \dfrac{x - vt}{\sqrt{1 - v^2/c^2}}. \label{eq10} \]
The postulates of relativity imply that the equation relating distance and time of the spherical wave front:
\[x^2 + y^2 + z^2 - c^2t^2 = 0 \nonumber \]
must apply both in terms of primed and unprimed coordinates, which was shown above to lead to Equation:
\[x^2 - c^2t^2 = x'^2 - c^2t'^2. \nonumber \]
We combine this with Equation \ref{eq10} that relates \(x\) and \(x′\) to obtain the relation between \(t\) and \(t'\):
\[t' = \dfrac{t - vx/c^2}{\sqrt{1 - v^2/c^2}}. \nonumber \]
The equations relating the time and position of the events as seen in \(S\) are then
\[ \begin{align*} t &= \dfrac{t' + vx'/c^2}{\sqrt{1 - v^2/c^2}}. \\[4pt] x &= \dfrac{x' + vt'}{\sqrt{1 - v^2/c^2}}. \\[4pt] y &= y' \\[4pt] z &= z'. \end {align*} \]
This set of equations, relating the position and time in the two inertial frames, is known as the Lorentz transformation. They are named in honor of H.A. Lorentz (1853–1928), who first proposed them. Interestingly, he justified the transformation on what was eventually discovered to be a fallacious hypothesis. The correct theoretical basis is Einstein’s special theory of relativity.
The reverse transformation expresses the variables in \(S\) in terms of those in S'. Simply interchanging the primed and unprimed variables and substituting gives:
\[\begin{align*} t'& = \dfrac{t - vx/c^2}{\sqrt{1 - v^2/c^2}} \\[4pt] x' &= \dfrac{x - vt}{\sqrt{1 - v^2/c^2}} \\[4pt] y' &= y \\[4pt] z' &= z. \end{align*} \nonumber \]
Spacecraft S' is on its way to Alpha Centauri when Spacecraft S passes it at relative speed \(c/2\). The captain of S' sends a radio signal that lasts 1.2 s according to that ship’s clock. Use the Lorentz transformation to find the time interval of the signal measured by the communications officer of spaceship S.
Solution
- Identify the known: \(\Delta t' = t'_2 - t'_1 = 1.2 s; \,\Delta x' = x'_2 - x'_1 = 0.\)
- Identify the unknown: \(\Delta t = t_2 - t_1\).
- Express the answer as an equation. The time signal starts as (\(x', t'_1\)) and stops at (\(x', t'_1\)). Note that the x' coordinate of both events is the same because the clock is at rest in S'. Write the first Lorentz transformation equation in terms of \(\Delta t = t_2 - t_1\), \(\Delta x = x_2 - x_1\), and similarly for the primed coordinates, as: \[\Delta t = \dfrac{\Delta t' + v\Delta x'/c^2}{\sqrt{1 - \dfrac{v^2}{c^2}}}. \nonumber \] Because the position of the clock in S' is fixed, \(\Delta x' = 0\), and the time interval \(\Delta t\) becomes: \[\Delta t = \dfrac{\Delta t'}{\sqrt{1 - \dfrac{v^2}{c^2}}}. \nonumber \]
- Do the calculation.
With \(\Delta t' = 1.2 \,s\) this gives: \[\begin{align*} \Delta t &= \dfrac{1.2 \,s}{\sqrt{1 - \left(\dfrac{1}{2}\right)^2}} \\[4pt] &= 1.4 \,s. \end{align*} \nonumber \] Note that the Lorentz transformation reproduces the time dilation equation.
A surveyor measures a street to be \(L = 100 \,m\) long in Earth frame \(S\). Use the Lorentz transformation to obtain an expression for its length measured from a spaceship \(S'\), moving by at speed \(0.20c\), assuming the \(x\) coordinates of the two frames coincide at time \(t = 0\).
Solution
- Identify the known: \(L = 100 \,m\); \(v = 0.20 c\); \(\Delta \tau = 0\).
- Identify the unknown: \(L'\).
- Express the answer as an equation. The surveyor in frame S has measured the two ends of the stick simultaneously, and found them at rest at \(x_2\) and \(x_1\) a distance \(L = x_2 - x_1 = 100 \,m\) apart. The spaceship crew measures the simultaneous location of the ends of the sticks in their frame. To relate the lengths recorded by observers in S' and S, respectively, write the second of the four Lorentz transformation equations as: \[\begin{align*} x_2 - x_1 &= \dfrac{x'_2 - vt}{\sqrt{1 - v^2/c^2}} - \dfrac{x'_1 - vt}{\sqrt{1 - v^2/c^2}} \\[4pt] &= \dfrac{x'_2 - x'_1}{\sqrt{1 - v^2/c^2}}. \end{align*} \nonumber \]
- Do the calculation. Because \(x_2 - x_1 = 100 \,m\), the length of the moving stick is equal to: \[\begin{align*} L' &= x'_2-x'_1 \\[4pt] &= (L)\sqrt{1 - v^2/c^2}\\[4pt] &= (100 \,m)\sqrt{1 - (0.20)^2} \\[4pt] &= 98.0 \,m. \end{align*} \nonumber \] Note that the Lorentz transformation gave the length contraction equation for the street.
The observer shown in Figure \(\PageIndex{2}\) standing by the railroad tracks sees the two bulbs flash simultaneously at both ends of the 26 m long passenger car when the middle of the car passes him at a speed of \(c/2\). Find the separation in time between when the bulbs flashed as seen by the train passenger seated in the middle of the car.
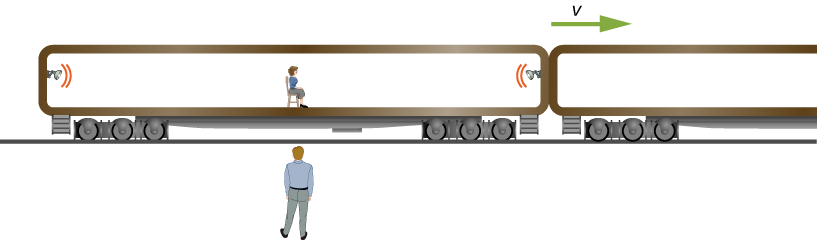
Solution
- Identify the known: \(\Delta t = 0\).
Note that the spatial separation of the two events is between the two lamps, not the distance of the lamp to the passenger.
- Identify the unknown: \(\Delta t' = t'_2 - t'_1.\).
Again, note that the time interval is between the flashes of the lamps, not between arrival times for reaching the passenger.
- Express the answer as an equation:
\[\Delta t = \dfrac{\Delta t' + v\Delta x'/c^2}{\sqrt{1 - v^2/c^2}}. \nonumber \]
- Do the calculation:
\[\begin{align*} 0 &= \dfrac{\Delta t' + \dfrac{c}{2} (26 \,m)/c^2}{\sqrt{1 - v^2/c^2}} \\[4pt] \Delta t' &= - \dfrac{26 \,m/s}{2c} = - \dfrac{26 \,m/s}{2(3.00 \times 10^8 \,m/s)} \\[4pt] &= -4.33 \times 10^{-8}\,s. \end{align*} \]
Significance
The sign indicates that the event with the larger \(x'_2\) namely, the flash from the right, is seen to occur first in the \(S′\) frame, as found earlier for this example, so that \(t_2 < t_1\).
Space-Time
Relativistic phenomena can be analyzed in terms of events in a four-dimensional space-time. When phenomena such as the twin paradox, time dilation, length contraction, and the dependence of simultaneity on relative motion are viewed in this way, they are seen to be characteristic of the nature of space and time, rather than specific aspects of electromagnetism.
In three-dimensional space, positions are specified by three coordinates on a set of Cartesian axes, and the displacement of one point from another is given by:
\[(\Delta x, \,\Delta y, \,\Delta z) = (x_2 - x_1, \,y_2 - y-1, \,z_2 - z_1). \nonumber \]
The distance \(\Delta r\) between the points is
\[\Delta r^2 = (\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2. \nonumber \]
The distance \(\Delta r\) is invariant under a rotation of axes. If a new set of Cartesian axes rotated around the origin relative to the original axes are used, each point in space will have new coordinates in terms of the new axes, but the distance \(\Delta r'\) given by
\[\Delta r'^2 = (\Delta x')^2 + (\Delta y')^2 + (\Delta z')^2. \nonumber \]
That has the same value that \(\Delta r^2\) had. Something similar happens with the Lorentz transformation in space-time.
Define the separation between two events, each given by a set of x, y, z¸ and ct along a four-dimensional Cartesian system of axes in space-time, as
\[(\Delta x, \,\Delta y, \,\Delta z, \,c\Delta t) = (x_2 - x_1, \,y_2 - y_1, \,z_2 - z_1, \,c(t_2 - t_1)). \nonumber \]
Also define the space-time interval \(Δs\) between the two events as
\[\Delta s^2 = (\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2 - (c\Delta t)^2. \nonumber \]
If the two events have the same value of ct in the frame of reference considered, \(\Delta s\) would correspond to the distance \(\Delta r\) between points in space.
The path of a particle through space-time consists of the events (x, y, z¸ ct) specifying a location at each time of its motion. The path through space-time is called the world line of the particle. The world line of a particle that remains at rest at the same location is a straight line that is parallel to the time axis. If the particle moves at constant velocity parallel to the x-axis, its world line would be a sloped line \(x = vt\), corresponding to a simple displacement vs. time graph. If the particle accelerates, its world line is curved. The increment of s along the world line of the particle is given in differential form as
\[ds^2 = (dx)^2 + (dy)^2 + (dz)^2 - c^2(dt)^2. \nonumber \]
Just as the distance \(\Delta r\) is invariant under rotation of the space axes, the space-time interval:
\[\Delta s^2 = (\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2 - (c\Delta t)^2. \nonumber \]
is invariant under the Lorentz transformation. This follows from the postulates of relativity, and can be seen also by substitution of the previous Lorentz transformation equations into the expression for the space-time interval:
\[\begin{align*} \Delta s^2 &= (\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2 - (c\Delta t)^2. \\[4pt] &=\left(\dfrac{\Delta x' + v\Delta t'}{\sqrt{1 - v^2/c^2}}\right)^2 + (\Delta y')^2 + (\Delta z')^2 - \left(c\dfrac{\Delta t' + \dfrac{v\Delta x'}{c^2}}{\sqrt{1 - v^2/c^2}}\right)^2 \\[4pt] &= (\Delta x')^2 + (\Delta y')^2 + (\Delta z')^2 - (c\Delta t')^2 \\[4pt] &= \Delta s'^2. \end{align*} \]
In addition, the Lorentz transformation changes the coordinates of an event in time and space similarly to how a three-dimensional rotation changes old coordinates into new coordinates:
|
Lorentz transformation (x, t coordinates): |
Axis–rotation around z - a axis (x, t coordinates): |
|---|---|
|
\(x' = (γ)x + (−βγ)ct\) |
\(x' = (\cos θ)x + (\sin θ)y\) |
| \(ct' = (−βγ)x + (γ)ct\) | \(y' = (−\sin θ)x + (\cos θ)y\) |
where \(\gamma = \dfrac{1}{\sqrt{1 - \beta^2}}\) and \(\beta = v/c\).
Lorentz transformations can be regarded as generalizations of spatial rotations to space-time. However, there are some differences between a three-dimensional axis rotation and a Lorentz transformation involving the time axis, because of differences in how the metric, or rule for measuring the displacements \(\Delta r\) and \(\Delta s\), differ. Although \(\Delta r\) is invariant under spatial rotations and \(\Delta s\) is invariant also under Lorentz transformation, the Lorentz transformation involving the time axis does not preserve some features, such as the axes remaining perpendicular or the length scale along each axis remaining the same.
Note that the quantity \(\Delta s^2\) can have either sign, depending on the coordinates of the space-time events involved. For pairs of events that give it a negative sign, it is useful to define \(c^2 \Delta \tau^2\) as \(-\Delta s^2\). The significance of \(c^2 \Delta \tau\) as just defined follows by noting that in a frame of reference where the two events occur at the same location, we have \(\Delta x = \Delta y = \Delta z = 0\) and therefore (from the equation for \(\Delta s^2 = - c^2 \Delta \tau^2\)):
\[c^2 \Delta \tau^2 = - \Delta s^2 = (c^2 \Delta t)^2. \nonumber \]
Therefore \(c^2 \Delta \tau\) is the time interval \(c^2 \Delta t\) in the frame of reference where both events occur at the same location. It is the same interval of proper time discussed earlier. It also follows from the relation between \(\Delta s\) and that \(c^2 \Delta \tau\) that because \(\Delta s\) is Lorentz invariant, the proper time is also Lorentz invariant. All observers in all inertial frames agree on the proper time intervals between the same two events.
Show that if a time increment \(dt\) elapses for an observer who sees the particle moving with velocity \(v\), it corresponds to a proper time particle increment for the particle of \(d\tau = \gamma dt\).
- Answer
-
Start with the definition of the proper time increment:
\[d\tau = \sqrt{-(ds)^2 /c^2} = \sqrt{dt^2 - (dx^2 + dx^2 + dx^2)/c^2}. \nonumber \]
where \((dx, dy, dx, cdt)\) are measured in the inertial frame of an observer who does not necessarily see that particle at rest. This therefore becomes
\[d\tau = \sqrt{-(ds)^2/c^2} = \sqrt{dt^2 - [(dx)^2 + (dy)^2 + (dz)^2]/c^2} \nonumber \]
\[dt\sqrt{1 - \left[ \left(\dfrac{dx}{dt}\right)^2 + \left(\dfrac{dy}{dt}\right)^2 + \left(\dfrac{dz}{dt}\right)^2\right] /c^2} \nonumber \]\[dt\sqrt{1 - v^2/c^2} \nonumber \]\[dt = \gamma d\tau. \nonumber \]
The Light Cone
We can deal with the difficulty of visualizing and sketching graphs in four dimensions by imagining the three spatial coordinates to be represented collectively by a horizontal axis, and the vertical axis to be the ct-axis. Starting with a particular event in space-time as the origin of the space-time graph shown, the world line of a particle that remains at rest at the initial location of the event at the origin then is the time axis. Any plane through the time axis parallel to the spatial axes contains all the events that are simultaneous with each other and with the intersection of the plane and the time axis, as seen in the rest frame of the event at the origin.
It is useful to picture a light cone on the graph, formed by the world lines of all light beams passing through the origin event A, as shown in Figure \(\PageIndex{3}\). The light cone, according to the postulates of relativity, has sides at an angle of 45° if the time axis is measured in units of ct, and, according to the postulates of relativity, the light cone remains the same in all inertial frames. Because the event A is arbitrary, every point in the space-time diagram has a light cone associated with it.
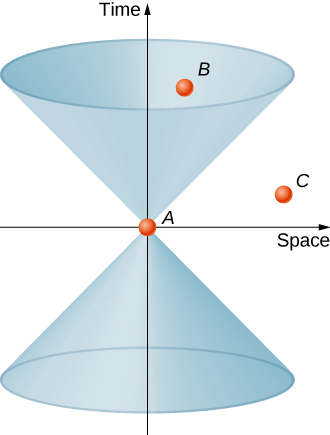
Consider now the world line of a particle through space-time. Any world line outside of the cone, such as one passing from A through C, would involve speeds greater than c, and would therefore not be possible. Events such as C that lie outside the light cone are said to have a space-like separation from event A. They are characterized by:
\[\Delta s_{AC}^2 = (x_A - x_C)^2 + (y_A - y_C)^2 + (z_A - z_C)^2 - (c\Delta t)^2 > 0. \nonumber \]
An event like B that lies in the upper cone is reachable without exceeding the speed of light in vacuum, and is characterized by
\[\Delta s_{AB}^2 = (x_A - x_B)^2 + (y_A - y_B)^2 + (z_A - z_B)^2 - (c\Delta t)^2 <0. \nonumber \]
The event is said to have a time-like separation from A. Time-like events that fall into the upper half of the light cone occur at greater values of t than the time of the event A at the vertex and are in the future relative to A. Events that have time-like separation from A and fall in the lower half of the light cone are in the past, and can affect the event at the origin. The region outside the light cone is labeled as neither past nor future, but rather as “elsewhere.”
For any event that has a space-like separation from the event at the origin, it is possible to choose a time axis that will make the two events occur at the same time, so that the two events are simultaneous in some frame of reference. Therefore, which of the events with space-like separation comes before the other in time also depends on the frame of reference of the observer. Since space-like separations can be traversed only by exceeding the speed of light; this violation of which event can cause the other provides another argument for why particles cannot travel faster than the speed of light, as well as potential material for science fiction about time travel. Similarly for any event with time-like separation from the event at the origin, a frame of reference can be found that will make the events occur at the same location. Because the relations
\[\Delta s_{AC}^2 = (x_A - x_C)^2 + (y_A - x_C)^2 + (z_A - z_C)^2 - (c\Delta t)^2 > 0. \nonumber \]
and
\[\Delta s_{AB}^2 = (x_A - x_B)^2 + (y_A - y_B)^2 + (z_A - z_B)^2 - (c\Delta t)^2 <0. \nonumber \]
are Lorentz invariant, whether two events are time-like and can be made to occur at the same place or space-like and can be made to occur at the same time is the same for all observers. All observers in different inertial frames of reference agree on whether two events have a time-like or space-like separation.
The twin paradox seen in space-time
The twin paradox discussed earlier involves an astronaut twin traveling at near light speed to a distant star system, and returning to Earth. Because of time dilation, the space twin is predicted to age much less than the earthbound twin. This seems paradoxical because we might have expected at first glance for the relative motion to be symmetrical and naively thought it possible to also argue that the earthbound twin should age less.
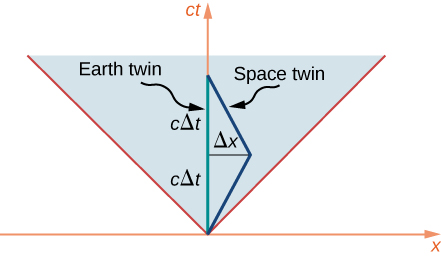
To analyze this in terms of a space-time diagram, assume that the origin of the axes used is fixed in Earth. The world line of the earthbound twin is then along the time axis.
The world line of the astronaut twin, who travels to the distant star and then returns, must deviate from a straight line path in order to allow a return trip. As seen in Figure \(\PageIndex{4}\), the circumstances of the two twins are not at all symmetrical. Their paths in space-time are of manifestly different length. Specifically, the world line of the earthbound twin has length \(2c\Delta t\), which then gives the proper time that elapses for the earthbound twin as \(2\Delta t\). The distance to the distant star system is \(\Delta x = v\Delta t\). The proper time that elapses for the space twin is \(2\Delta \tau\) where
\[c^2\Delta \tau^2 = - \Delta s^2 = (c\Delta t)^2 - (\Delta x)^2. \nonumber \]
This is considerably shorter than the proper time for the earthbound twin by the ratio
\[\dfrac{c\Delta \tau}{c\Delta t} = \sqrt{\dfrac{(c\Delta t)^2 - (\Delta x)^2}{(c\Delta t)^2}} = \sqrt{\dfrac{(c\Delta t)^2 - (v\Delta t)^2}{(c\Delta t)^2}} = \sqrt{1 - \dfrac{v^2}{c^2}} = \dfrac{1}{\gamma}. \nonumber \]
consistent with the time dilation formula. The twin paradox is therefore seen to be no paradox at all. The situation of the two twins is not symmetrical in the space-time diagram. The only surprise is perhaps that the seemingly longer path on the space-time diagram corresponds to the smaller proper time interval, because of how \(\Delta \tau\) and \(\Delta s\) depend on \(\Delta x\) and \(\Delta t\).
Lorentz Transformations in Space-time
We have already noted how the Lorentz transformation leaves
\[\Delta s^2 = (\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2 - (c\Delta t)^2. \nonumber \]
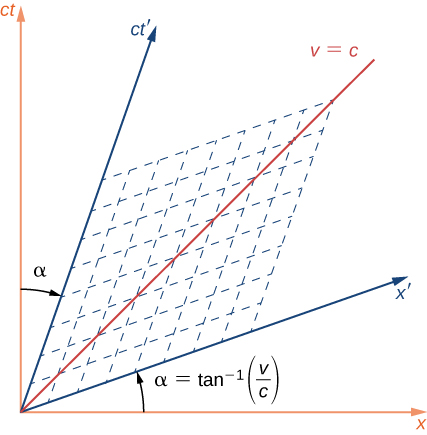
unchanged and corresponds to a rotation of axes in the four-dimensional space-time. If the S and S' frames are in relative motion along their shared x-direction the space and time axes of S' are rotated by an angle αα as seen from S, in the way shown in shown in Figure \(\PageIndex{5}\), where:
\[tan \,\alpha = \dfrac{v}{c} = \beta. \nonumber \]
This differs from a rotation in the usual three-dimension sense, insofar as the two space-time axes rotate toward each other symmetrically in a scissors-like way, as shown. The rotation of the time and space axes are both through the same angle. The mesh of dashed lines parallel to the two axes show how coordinates of an event would be read along the primed axes. This would be done by following a line parallel to the x' and one parallel to the t'-axis, as shown by the dashed lines. The length scale of both axes are changed by:
\[ct' = ct\sqrt{\dfrac{1 + \beta^2}{1 - \beta^2}}; \,x' = x\sqrt{\dfrac{1 + \beta^2}{1 - \beta^2}}. \nonumber \]
The line labeled “v = c” at 45° to the x-axis corresponds to the edge of the light cone, and is unaffected by the Lorentz transformation, in accordance with the second postulate of relativity. The “v = c” line, and the light cone it represents, are the same for both the S and S' frame of reference.
Simultaneity
Simultaneity of events at separated locations depends on the frame of reference used to describe them, as given by the scissors-like “rotation” to new time and space coordinates as described. If two events have the same \(t\) values in the unprimed frame of reference, they need not have the same values measured along the \(ct'\)-axis, and would then not be simultaneous in the primed frame.
As a specific example, consider the near-light-speed train in which flash lamps at the two ends of the car have flashed simultaneously in the frame of reference of an observer on the ground. The space-time graph is shown Figure \(\PageIndex{6}\). The flashes of the two lamps are represented by the dots labeled “Left flash lamp” and “Right flash lamp” that lie on the light cone in the past. The world line of both pulses travel along the edge of the light cone to arrive at the observer on the ground simultaneously. Their arrival is the event at the origin. They therefore had to be emitted simultaneously in the unprimed frame, as represented by the point labeled as \(t\) (both). But time is measured along the ct'-axis in the frame of reference of the observer seated in the middle of the train car. So in her frame of reference, the emission event of the bulbs labeled as \(t'\) (left) and \(t'\) (right) were not simultaneous.
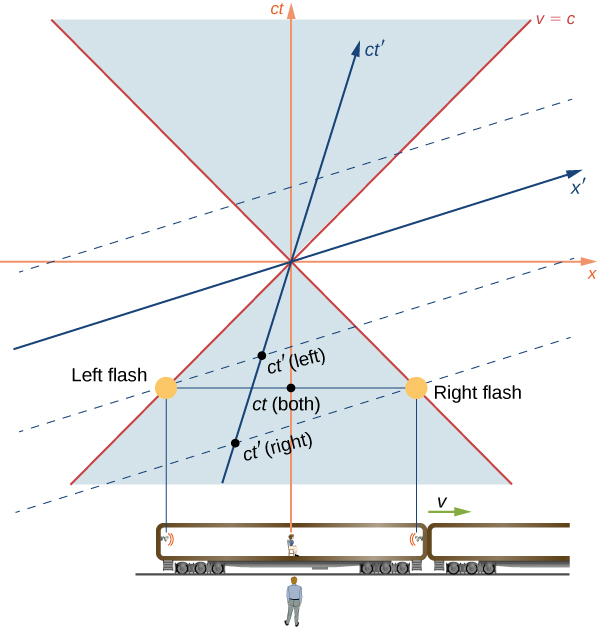
In terms of the space-time diagram, the two observers are merely using different time axes for the same events because they are in different inertial frames, and the conclusions of both observers are equally valid. As the analysis in terms of the space-time diagrams further suggests, the property of how simultaneity of events depends on the frame of reference results from the properties of space and time itself, rather than from anything specifically about electromagnetism.


