1.3: Thermometers and Temperature Scales
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of this section, you will be able to:
- Describe several different types of thermometers
- Convert temperatures between the Celsius, Fahrenheit, and Kelvin scales
Any physical property that depends consistently and reproducibly on temperature can be used as the basis of a thermometer. For example, volume increases with temperature for most substances. This property is the basis for the common alcohol thermometer and the original mercury thermometers. Other properties used to measure temperature include electrical resistance, color, and the emission of infrared radiation (Figure 1.3.1).
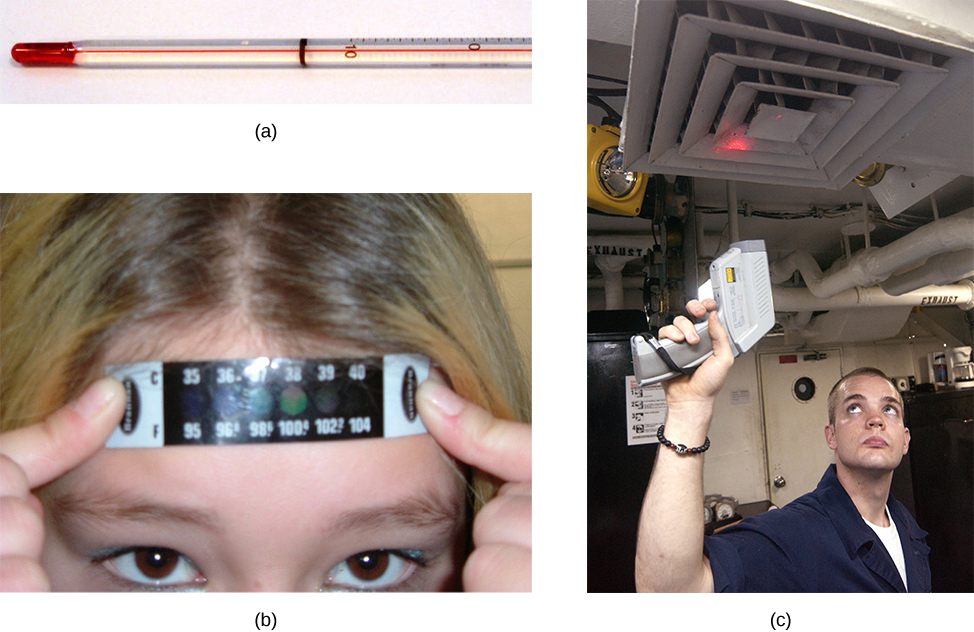
Thermometers measure temperature according to well-defined scales of measurement. The three most common temperature scales are Fahrenheit, Celsius, and Kelvin. Temperature scales are created by identifying two reproducible temperatures. The freezing and boiling temperatures of water at standard atmospheric pressure are commonly used.
On the Celsius scale, the freezing point of water is 0oC and the boiling point is 100oC. The unit of temperature on this scale is the degree Celsius (oC). The Fahrenheit scale (still the most frequently used for common purposes in the United States) has the freezing point of water at 32oF and the boiling point a. 212oF Its unit is the degree Fahrenheit (oF). You can see that 100 Celsius degrees span the same range as 180 Fahrenheit degrees. Thus, a temperature difference of one degree on the Celsius scale is 1.8 times as large as a difference of one degree on the Fahrenheit scale, or
ΔTF=95ΔTC.
The definition of temperature in terms of molecular motion suggests that there should be a lowest possible temperature, where the average kinetic energy of molecules is zero (or the minimum allowed by quantum mechanics). Experiments confirm the existence of such a temperature, called absolute zero. An absolute temperature scale is one whose zero point is absolute zero. Such scales are convenient in science because several physical quantities, such as the volume of an ideal gas, are directly related to absolute temperature.
The Kelvin scale is the absolute temperature scale that is commonly used in science. The SI temperature unit is the kelvin, which is abbreviated K (not accompanied by a degree sign). Thus 0 K is absolute zero. The freezing and boiling points of water are 273.15 K and 373.15 K, respectively. Therefore, temperature differences are the same in units of kelvins and degrees Celsius, or ΔTC=ΔTK.

The relationships between the three common temperature scales are shown in Figure 1.3.2. Temperatures on these scales can be converted using the equations in Table 1.3.1.
| To convert from… | Use this equation… |
|---|---|
| Celsius to Fahrenheit | TF=95TC+32 |
| Fahrenheit to Celsius | TC=59(TF−32) |
| Celsius to Kelvin | TK=TC+273.15 |
| Kelvin to Celsius | TC=TK−273.15 |
| Fahrenheit to Kelvin | TK=59(TF−32)+273.15 |
| Kelvin to Fahrenheit | TF=95(TK−273.15)+32 |
To convert between Fahrenheit and Kelvin, convert to Celsius as an intermediate step.
“Room temperature” is generally defined in physics to be 25oC. (a) What is room temperature in oF? (b) What is it in K?
Strategy To answer these questions, all we need to do is choose the correct conversion equations and substitute the known values.
Solution
To convert from oC to oF, use the equation
TF=95TC+32.
Substitute the known value into the equation and solve:
TF=95(25oC)+32=77oF.
Similarly, we find that TK=TC+273.15=298K.
The Kelvin scale is part of the SI system of units, so its actual definition is more complicated than the one given above. First, it is not defined in terms of the freezing and boiling points of water, but in terms of the triple point. The triple point is the unique combination of temperature and pressure at which ice, liquid water, and water vapor can coexist stably. As will be discussed in the section on phase changes, the coexistence is achieved by lowering the pressure and consequently the boiling point to reach the freezing point. The triple-point temperature is defined as 273.16 K. This definition has the advantage that although the freezing temperature and boiling temperature of water depend on pressure, there is only one triple-point temperature.
Second, even with two points on the scale defined, different thermometers give somewhat different results for other temperatures. Therefore, a standard thermometer is required. Metrologists (experts in the science of measurement) have chosen the constant-volume gas thermometer for this purpose. A vessel of constant volume filled with gas is subjected to temperature changes, and the measured temperature is proportional to the change in pressure. Using “TP” to represent the triple point,
T=ppTPTTP.
The results depend somewhat on the choice of gas, but the less dense the gas in the bulb, the better the results for different gases agree. If the results are extrapolated to zero density, the results agree quite well, with zero pressure corresponding to a temperature of absolute zero.
Constant-volume gas thermometers are big and come to equilibrium slowly, so they are used mostly as standards to calibrate other thermometers.


