13.2: Faraday’s Law
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of this section, you will be able to:
- Determine the magnetic flux through a surface, knowing the strength of the magnetic field, the surface area, and the angle between the normal to the surface and the magnetic field
- Use Faraday’s law to determine the magnitude of induced emf in a closed loop due to changing magnetic flux through the loop
The first productive experiments concerning the effects of time-varying magnetic fields were performed by Michael Faraday in 1831. One of his early experiments is represented in Figure 13.2.1. An emf is induced when the magnetic field in the coil is changed by pushing a bar magnet into or out of the coil. Emfs of opposite signs are produced by motion in opposite directions, and the directions of emfs are also reversed by reversing poles. The same results are produced if the coil is moved rather than the magnet—it is the relative motion that is important. The faster the motion, the greater the emf, and there is no emf when the magnet is stationary relative to the coil.
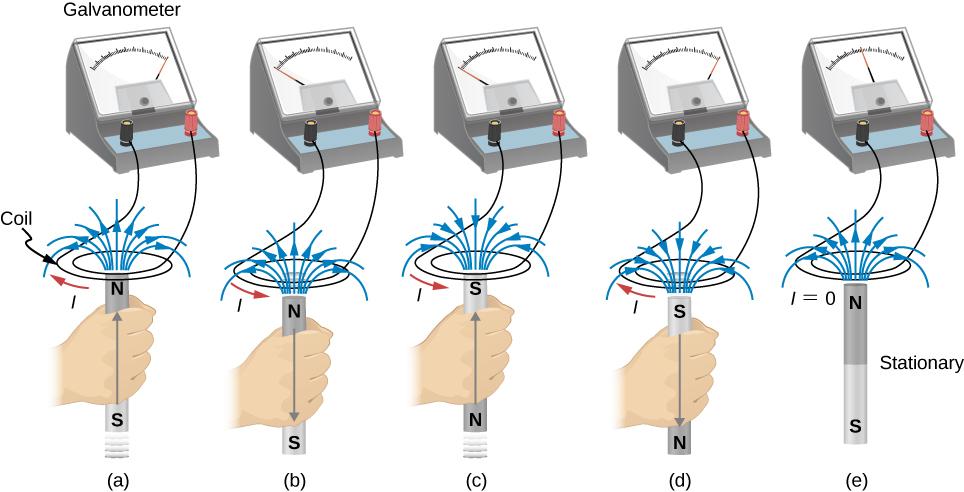
Faraday also discovered that a similar effect can be produced using two circuits—a changing current in one circuit induces a current in a second, nearby circuit. For example, when the switch is closed in circuit 1 of Figure 13.2.1a, the ammeter needle of circuit 2 momentarily deflects, indicating that a short-lived current surge has been induced in that circuit. The ammeter needle quickly returns to its original position, where it remains. However, if the switch of circuit 1 is now suddenly opened, another short-lived current surge in the direction opposite from before is observed in circuit 2.
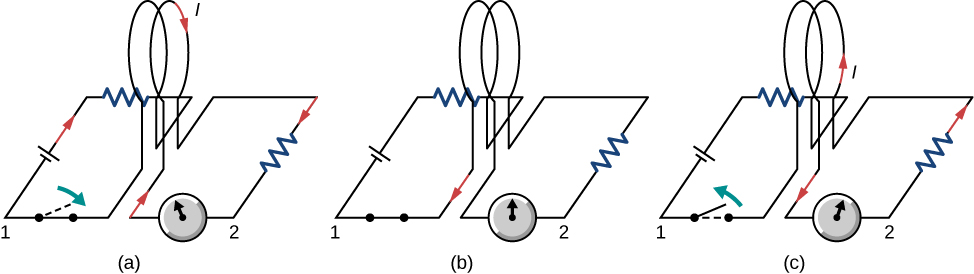
Faraday realized that in both experiments, a current flowed in the circuit containing the ammeter only when the magnetic field in the region occupied by that circuit was changing. As the magnet of the figure was moved, the strength of its magnetic field at the loop changed; and when the current in circuit 1 was turned on or off, the strength of its magnetic field at circuit 2 changed. Faraday was eventually able to interpret these and all other experiments involving magnetic fields that vary with time in terms of the following law.
The emf ϵ induced is the negative change in the magnetic flux Φm per unit time. Any change in the magnetic field or change in orientation of the area of the coil with respect to the magnetic field induces a voltage (emf).
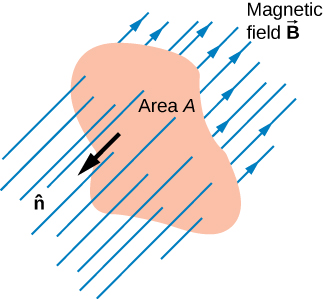
The magnetic flux is a measurement of the amount of magnetic field lines through a given surface area, as seen in Figure 13.2.3. This definition is similar to the electric flux studied earlier. This means that if we have
Φm=∫S→B⋅ˆndA,
then the induced emf or the voltage generated by a conductor or coil moving in a magnetic field is
ϵ=−ddt∫S→B⋅ˆndA=−dΦmdt.
The negative sign describes the direction in which the induced emf drives current around a circuit. However, that direction is most easily determined with a rule known as Lenz’s law, which we will discuss shortly.
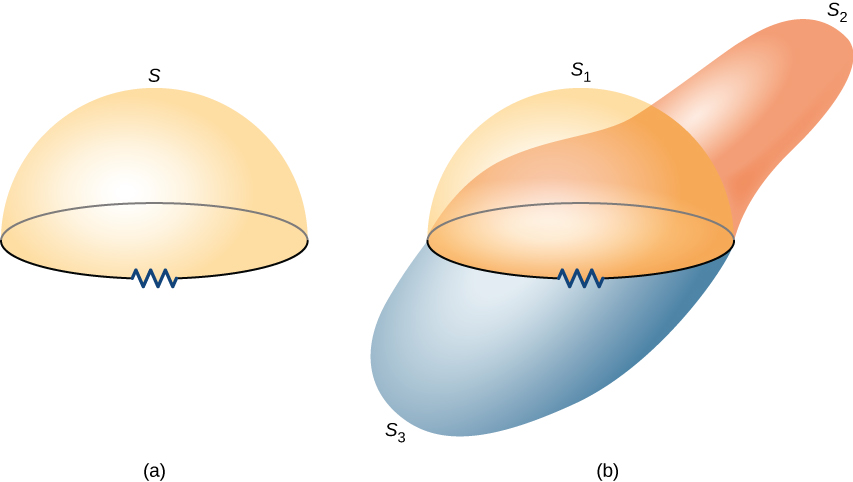
13.2.1a depicts a circuit and an arbitrary surface S that it bounds. Notice that S is an open surface. It can be shown that any open surface bounded by the circuit in question can be used to evaluate Φm. For example, Φm is the same for the various surfaces S1,S2,... of part (b) of the figure.
The SI unit for magnetic flux is the weber (Wb),
1Wb=1T⋅m2.
Occasionally, the magnetic field unit is expressed as webers per square meter ( Wb/m2) instead of teslas, based on this definition. In many practical applications, the circuit of interest consists of a number N of tightly wound turns (Figure 13.2.5). Each turn experiences the same magnetic flux. Therefore, the net magnetic flux through the circuits is N times the flux through one turn, and Faraday’s law is written as
ϵ=−ddt(NΦm)=−NdΦmdt.
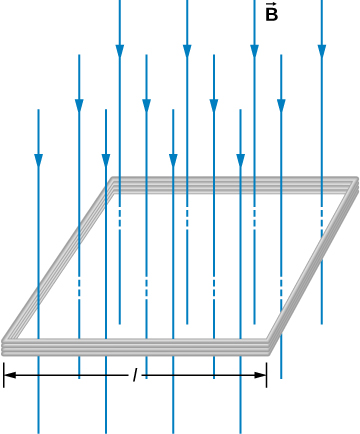
The square coil of Figure 13.2.1 has sides l=0.25m long and is tightly wound with N=200 turns of wire. The resistance of the coil is R=5.0Ω The coil is placed in a spatially uniform magnetic field that is directed perpendicular to the face of the coil and whose magnitude is decreasing at a rate dB/dt=−0.040T/s. (a) What is the magnitude of the emf induced in the coil? (b) What is the magnitude of the current circulating through the coil?
Strategy
The area vector, or ˆn direction, is perpendicular to area covering the loop. We will choose this to be pointing downward so that →B is parallel to ˆn and that the flux turns into multiplication of magnetic field times area. The area of the loop is not changing in time, so it can be factored out of the time derivative, leaving the magnetic field as the only quantity varying in time. Lastly, we can apply Ohm’s law once we know the induced emf to find the current in the loop.
Solution
- The flux through one turn is Φm=BA=Bt2,
so we can calculate the magnitude of the emf from Faraday’s law. The sign of the emf will be discussed in the next section, on Lenz’s law: |ϵ|=|−NdΦmdt|=Nl2dBdt
- The magnitude of the current induced in the coil is I=ϵR=0.50V5.0Ω=0.10A.
Significance
If the area of the loop were changing in time, we would not be able to pull it out of the time derivative. Since the loop is a closed path, the result of this current would be a small amount of heating of the wires until the magnetic field stops changing. This may increase the area of the loop slightly as the wires are heated.
A closely wound coil has a radius of 4.0 cm, 50 turns, and a total resistance of 40Ω. At what rate must a magnetic field perpendicular to the face of the coil change in order to produce Joule heating in the coil at a rate of 2.0 mW?
Solution
1.1 T/s


