15.3: Simple AC Circuits
- Page ID
- 4443
By the end of the section, you will be able to:
- Interpret phasor diagrams and apply them to ac circuits with resistors, capacitors, and inductors
- Define the reactance for a resistor, capacitor, and inductor to help understand how current in the circuit behaves compared to each of these devices
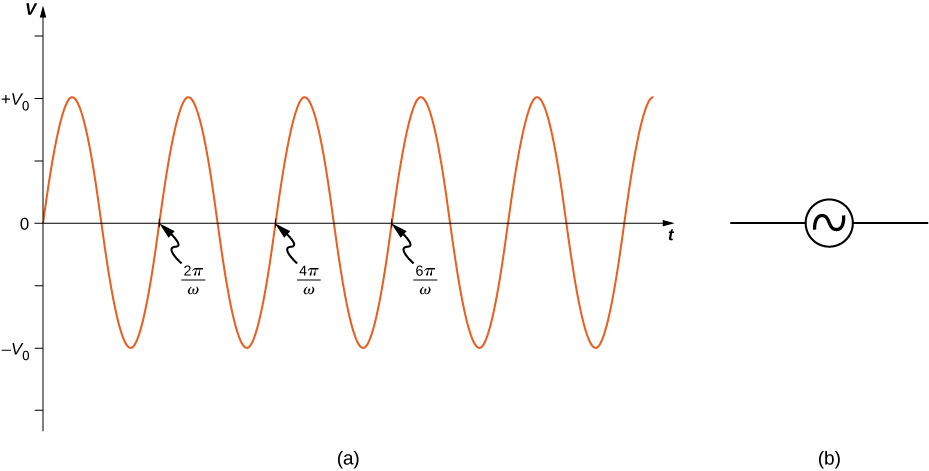
In this section, we study simple models of ac voltage sources connected to three circuit components: (1) a resistor, (2) a capacitor, and (3) an inductor. The power furnished by an ac voltage source has an emf given by
\[v(t) = V_0 \, sin \, \omega t,\]
as shown in Figure \(\PageIndex{1}\). This sine function assumes we start recording the voltage when it is \(v = 0 \, V\) at a time of \(t = 0 \, s\). A phase constant may be involved that shifts the function when we start measuring voltages, similar to the phase constant in the waves we studied in Waves. However, because we are free to choose when we start examining the voltage, we can ignore this phase constant for now. We can measure this voltage across the circuit components using one of two methods: (1) a quantitative approach based on our knowledge of circuits, or (2) a graphical approach that is explained in the coming sections.
Resistor
First, consider a resistor connected across an ac voltage source. From Kirchhoff’s loop rule, the instantaneous voltage across the resistor of Figure \(\PageIndex{2a}\) is
\[v_R(t) = V_0 \, sin \, \omega t\]
and the instantaneous current through the resistor is
\[i_R(t) = \frac{v_R(t)}{R} = \frac{V_0}{R} \, sin \, \omega t = I_0 \, sin \, \omega t.\]
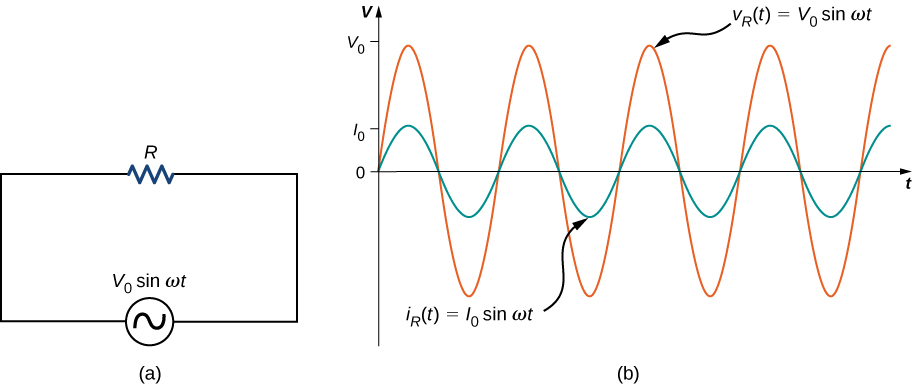
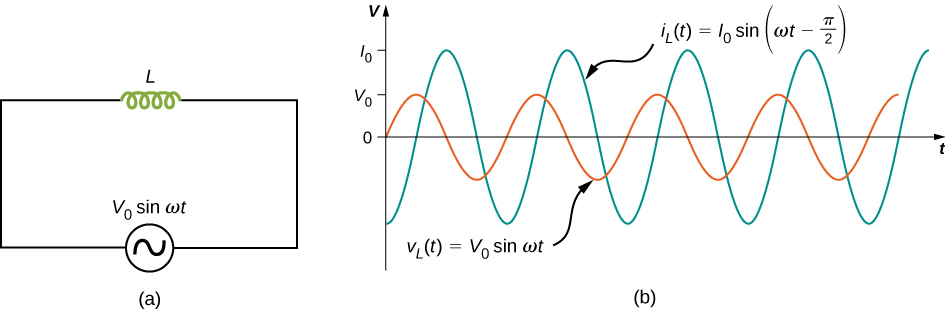
Here, \(I_0 = V_0/R\) is the amplitude of the time-varying current. Plots of \(i_R(t)\) and \(v_R(t)\) are shown in Figure \(\PageIndex{2b}\). Both curves reach their maxima and minima at the same times, that is, the current through and the voltage across the resistor are in phase.
Graphical representations of the phase relationships between current and voltage are often useful in the analysis of ac circuits. Such representations are called phasor diagrams. The phasor diagram for \(i_R(t)\) is shown in Figure \(\PageIndex{3a}\), with the current on the vertical axis. The arrow (or phasor) is rotating counterclockwise at a constant angular frequency \(\omega\), so we are viewing it at one instant in time. If the length of the arrow corresponds to the current amplitude \(I_0\), the projection of the rotating arrow onto the vertical axis is \(i_R(t) = I_0 \, sin \, \omega t\), which is the instantaneous current.
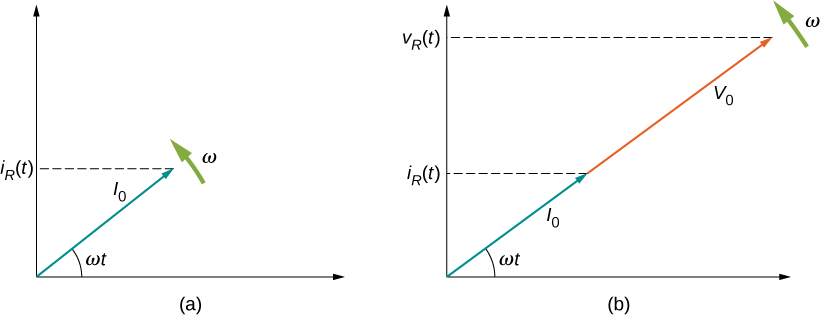
The vertical axis on a phasor diagram could be either the voltage or the current, depending on the phasor that is being examined. In addition, several quantities can be depicted on the same phasor diagram. For example, both the current \(i_R(t)\) and the voltage \(v_R(t)\) are shown in the diagram of Figure \(\PageIndex{3b}\). Since they have the same frequency and are in phase, their phasors point in the same direction and rotate together. The relative lengths of the two phasors are arbitrary because they represent different quantities; however, the ratio of the lengths of the two phasors can be represented by the resistance, since one is a voltage phasor and the other is a current phasor.
Capacitor
Now let’s consider a capacitor connected across an ac voltage source. From Kirchhoff’s loop rule, the instantaneous voltage across the capacitor of Figure \(\PageIndex{4a}\) is
\[v_C(t) = V_0 \, sin \, \omega t.\]
Recall that the charge in a capacitor is given by \(Q = CV\). This is true at any time measured in the ac cycle of voltage. Consequently, the instantaneous charge on the capacitor is
\[q(t) = Cv_C(t) = CV_0 \, sin \, \omega t.\]
Since the current in the circuit is the rate at which charge enters (or leaves) the capacitor,
\[i_C(t) = \frac{dq(t)}{dt} = \omega CV_0 \, cos \, \omega t = I_0 \, cos \, \omega t,\]
where \(I_0 = \omega CV_0\) is the current amplitude. Using the trigonometric relationship \(cos \, \omega t = sin (\omega t + \pi/2)\), we may express the instantaneous current as
\[i_C(t) = I_0 \, sin \left(\omega t + \frac{\pi}{2}\right).\]
Dividing \(V_0\) by \(I_0\), we obtain an equation that looks similar to Ohm’s law:
\[\frac{V_0}{I_0} = \frac{1}{\omega C} = X_C. \label{15.3}\]
The quantity \(X_C\) is analogous to resistance in a dc circuit in the sense that both quantities are a ratio of a voltage to a current. As a result, they have the same unit, the ohm. Keep in mind, however, that a capacitor stores and discharges electric energy, whereas a resistor dissipates it. The quantity \(X_C\) is known as the capacitive reactance of the capacitor, or the opposition of a capacitor to a change in current. It depends inversely on the frequency of the ac source—high frequency leads to low capacitive reactance.
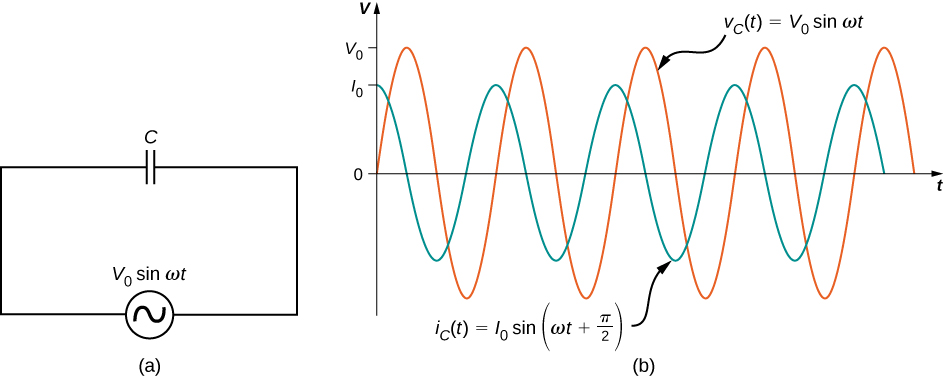
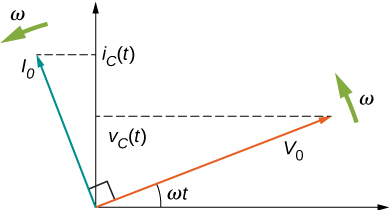
A comparison of the expressions for \(v_C(t)\) and \(i_C(t)\) shows that there is a phase difference of \(\pi/2\) rad between them. When these two quantities are plotted together, the current peaks a quarter cycle (or \(\pi/2\) rad) ahead of the voltage, as illustrated in Figure \(\PageIndex{4b}\). The current through a capacitor leads the voltage across a capacitor by \(\pi/2\) rad, or a quarter of a cycle.
The corresponding phasor diagram is shown in Figure \(\PageIndex{5}\). Here, the relationship between \(i_C(t)\) and \(v_C(t)\) is represented by having their phasors rotate at the same angular frequency, with the current phasor leading by \(\pi/2\) rad.
To this point, we have exclusively been using peak values of the current or voltage in our discussion, namely, \(I_0\) and \(V_0\). However, if we average out the values of current or voltage, these values are zero. Therefore, we often use a second convention called the root mean square value, or rms value, in discussions of current and voltage. The rms operates in reverse of the terminology. First, you square the function, next, you take the mean, and then, you find the square root. As a result, the rms values of current and voltage are not zero. Appliances and devices are commonly quoted with rms values for their operations, rather than peak values. We indicate rms values with a subscript attached to a capital letter (such as \(I_{rms}\)).
Although a capacitor is basically an open circuit, an rms current, or the root mean square of the current, appears in a circuit with an ac voltage applied to a capacitor. Consider that
\[I_{rms} = \frac{I_0}{\sqrt{2}},\]
where \(I_0\) is the peak current in an ac system. The rms voltage, or the root mean square of the voltage, is
\[V_{rms} = \frac{V_0}{\sqrt{2}},\]
where \(V_0\) is the peak voltage in an ac system. The rms current appears because the voltage is continually reversing, charging, and discharging the capacitor. If the frequency goes to zero, which would be a dc voltage, \(X_C\) tends to infinity, and the current is zero once the capacitor is charged. At very high frequencies, the capacitor’s reactance tends to zero—it has a negligible reactance and does not impede the current (it acts like a simple wire).
Inductor
Lastly, let’s consider an inductor connected to an ac voltage source. From Kirchhoff’s loop rule, the voltage across the inductor L of Figure \(\PageIndex{6a}\) is
\[v_L(t) = V_0 \, sin \, \omega t. \label{15.6}\]
The emf across an inductor is equal to \(\epsilon = - L(di_L/dt)\); however, the potential difference across the inductor is \(v_L(t) = Ldi_L(t)/dt\), because if we consider that the voltage around the loop must equal zero, the voltage gained from the ac source must dissipate through the inductor. Therefore, connecting this with the ac voltage source, we have
\[\frac{di_L(t)}{dt} = \frac{V_0}{L} \, sin \, \omega t.\]
The current \(i_L(t)\) is found by integrating this equation. Since the circuit does not contain a source of constant emf, there is no steady current in the circuit. Hence, we can set the constant of integration, which represents the steady current in the circuit, equal to zero, and we have
\[i_L(t) = - \frac{V_0}{\omega L} cos \, \omega t = \frac{V_0}{\omega L} sin \left(\omega t - \frac{\pi}{2}\right) = I_0 \, sin \left(\omega t - \frac{\pi}{2}\right), \label{15.7}\]
where \(I_0 = V_0/\omega L\). The relationship between \(V_0\) and \(I_0\) may also be written in a form analogous to Ohm’s law:
\[\frac{V_0}{I_0} = \omega L = X_L. \label{15.8}\]
The quantity \(X_L\) is known as the inductive reactance of the inductor, or the opposition of an inductor to a change in current; its unit is also the ohm. Note that \(X_L\) varies directly as the frequency of the ac source—high frequency causes high inductive reactance.
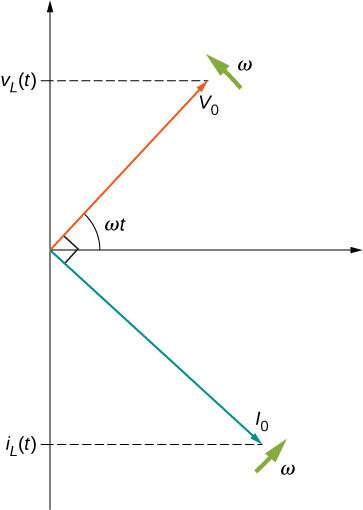
A phase difference of \(\pi/2\) rad occurs between the current through and the voltage across the inductor. From Equation \ref{15.6} and Equation \ref{15.7}, the current through an inductor lags the potential difference across an inductor by \(\pi/2\) rad, or a quarter of a cycle. The phasor diagram for this case is shown in Figure \(\PageIndex{7}\).
An animation from the University of New South Wales AC Circuits illustrates some of the concepts we discuss in this chapter. They also include wave and phasor diagrams that evolve over time so that you can get a better picture of how each changes over time.
An ac generator produces an emf of amplitude 10 V at a frequency \(f = 60 \, Hz\). Determine the voltages across and the currents through the circuit elements when the generator is connected to (a) a \(100 \, \Omega\) resistor, (b) a \(10 \, \mu F\) capacitor, and (c) a 15-mH inductor.
Strategy
The entire AC voltage across each device is the same as the source voltage. We can find the currents by finding the reactance X of each device and solving for the peak current using \(I_0 = V_0/X\).
Solution
The voltage across the terminals of the source is
\[v(t) = V_0 \, sin \, \omega t = (10 \, V) sin \, 120 \pi t,\]
where \(\omega = 2\pi f = 120 \pi \, rad/s\) is the angular frequency. Since v(t) is also the voltage across each of the elements, we have
\[v(t) = v_R(t) = v_C(t) = v_L(t) = (10 \, V) sin \, 120 \pi t.\]
a. When \(R = 100 \, \Omega\), the amplitude of the current through the resistor is
\[I_0 = V_0/R = 10 \, V/100 \, \Omega = 0.10 \, A,\] so
\[i_R(t) = (0.10 \, A) sin \, 120 \pi t.\]
b. From Equation \ref{15.3}, the capacitive reactance is
\[X_C = \frac{1}{\omega C} = \frac{1}{(120 \pi \, rad/s)(10 \times 10^{-6}F)} = 265 \, \Omega,\]
so the maximum value of the current is
\[I_0 = \frac{V_0}{X_C} = \frac{10 \, V}{265 \, \Omega} = 3.8 \times 10^{-2} \, A\]
and the instantaneous current is given by
\[i_C(t) = (3.8 \times 10^{-2} \, A) \, sin \, \left(120 \pi t + \frac{\pi}{2}\right).\]
c. From Equation \ref{15.8}, the inductive reactance is
\[ X_L = \omega L = (120 \pi \, rad/s)(15 \times 10^{-3} H) = 5.7 \, \Omega.\]
The maximum current is therefore
\[I_0 = \frac{10 \, V}{5.7 \, \Omega} = 1.8 \, A\]
and the instantaneous current is
\[i_L(t) = (1.8 \, A) \, sin \left(120 \pi t - \frac{\pi}{2}\right).\]
Significance
Although the voltage across each device is the same, the peak current has different values, depending on the reactance. The reactance for each device depends on the values of resistance, capacitance, or inductance.
Repeat Example \(\PageIndex{1}\) for an ac source of amplitude 20 V and frequency 100 Hz.
- Answer
-
a. \((20 \, V) \, sin \, 200 \pi t\), \((0.20 \, A) \, sin \, 200 \pi t\);
b. \((20 \, V) \, sin \, 200 \pi t\), \((0.13 \, A) \, sin \, (200\pi t + \pi /2)\);
c. \((20 \, V) \, sin \, 200 \pi t\), \((2.1 \, A) \, sin \, (200 \pi t - \pi/2)\)
Contributors and Attributions
Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University), and Bill Moebs with many contributing authors. This work is licensed by OpenStax University Physics under a Creative Commons Attribution License (by 4.0).


