8.2: Potential Energy of a System
( \newcommand{\kernel}{\mathrm{null}\,}\)
- Relate the difference of potential energy to work done on a particle for a system without friction or air drag
- Explain the meaning of the zero of the potential energy function for a system
- Calculate and apply the gravitational potential energy for an object near Earth’s surface and the elastic potential energy of a mass-spring system
In Work, we saw that the work done on an object by the constant gravitational force, near the surface of Earth, over any displacement is a function only of the difference in the positions of the end-points of the displacement. This property allows us to define a different kind of energy for the system than its kinetic energy, which is called potential energy. We consider various properties and types of potential energy in the following subsections.
Potential Energy Basics
In Motion in Two and Three Dimensions, we analyzed the motion of a projectile, like kicking a football in Figure 8.2.1. For this example, let’s ignore friction and air resistance. As the football rises, the work done by the gravitational force on the football is negative, because the ball’s displacement is positive vertically and the force due to gravity is negative vertically. We also noted that the ball slowed down until it reached its highest point in the motion, thereby decreasing the ball’s kinetic energy. This loss in kinetic energy translates to a gain in gravitational potential energy of the football-Earth system.
As the football falls toward Earth, the work done on the football is now positive, because the displacement and the gravitational force both point vertically downward. The ball also speeds up, which indicates an increase in kinetic energy. Therefore, energy is converted from gravitational potential energy back into kinetic energy.
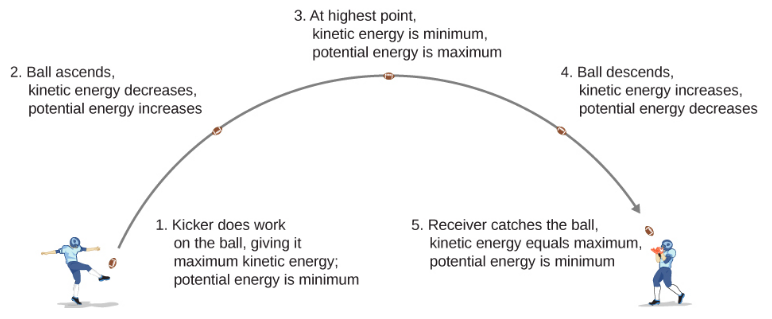
Based on this scenario, we can define the difference of potential energy from point A to point B as the negative of the work done:
ΔUAB=UB−UA=−WAB
This formula explicitly states a potential energy difference, not just an absolute potential energy. Therefore, we need to define potential energy at a given position in such a way as to state standard values of potential energy on their own, rather than potential energy differences. We do this by rewriting the potential energy function in terms of an arbitrary constant,
ΔU=U(→r)−U(→r0)
The choice of the potential energy at a starting location of →r0 is made out of convenience in the given problem. Most importantly, whatever choice is made should be stated and kept consistent throughout the given problem. There are some well-accepted choices of initial potential energy. For example, the lowest height in a problem is usually defined as zero potential energy, or if an object is in space, the farthest point away from the system is often defined as zero potential energy. Then, the potential energy, with respect to zero at →r0, is just U(→r).
As long as there is no friction or air resistance, the change in kinetic energy of the football equals negative of the change in gravitational potential energy of the football. This can be generalized to any potential energy:
ΔKAB=−ΔUAB
Let’s look at a specific example, choosing zero potential energy for gravitational potential energy at convenient points.
A particle moves along the x-axis under the action of a force given by F = -ax2, where a = 3 N/m2. (a) What is the difference in its potential energy as it moves from xA = 1 m to xB = 2 m? (b) What is the particle’s potential energy at x = 1 m with respect to a given 0.5 J of potential energy at x=0?
Strategy
(a) The difference in potential energy is the negative of the work done, as defined by Equation ???. The work is defined in the previous chapter as the dot product of the force with the distance. Since the particle is moving forward in the x-direction, the dot product simplifies to a multiplication (ˆi⋅ˆi = 1). To find the total work done, we need to integrate the function between the given limits. After integration, we can state the work or the change in potential energy. (b) The potential energy function, with respect to zero at x=0, is the indefinite integral encountered in part (a), with the constant of integration determined from Equation ???. Then, we substitute the x-value into the function of potential energy to calculate the potential energy at x = 1.
Solution
a. The work done by the given force as the particle moves from coordinate x to x + dx in one dimension is
dW=→F⋅d→r=Fdx=−ax2dx
Substituting this expression into Equation ???, we obtain
ΔU=−W=∫x2x1ax2dx=13(3N/m2)x3|2m1m=7J
b. The indefinite integral for the potential energy function in part (a) is
U(x)=13ax3+ const. ,
and we want the constant to be determined by
U(0)=0.5J.
Thus, the potential energy with respect to zero at x = 0 is just
U(x)=13ax3+0.5J
Therefore, the potential energy at x = 1 m is
U(1m)=13(3N/m2)(1m)3+0.5J=1.5J.
Significance
In this one-dimensional example, any function we can integrate, independent of path, is conservative. Notice how we applied the definition of potential energy difference to determine the potential energy function with respect to zero at a chosen point. Also notice that the potential energy, as determined in part (b), at x = 1 m is U(1 m) = 1 J and at x = 2 m is U(2 m) = 8 J; their difference is the result in part (a).
In Example 8.2.1, what are the potential energies of the particle at x = 1 m and x = 2 m with respect to zero at x = 1.5 m? Verify that the difference of potential energy is still 7 J.
Systems of Several Particles
In general, a system of interest could consist of several particles. The difference in the potential energy of the system is the negative of the work done by gravitational or elastic forces, which, as we will see in the next section, are conservative forces. The potential energy difference depends only on the initial and final positions of the particles, and on some parameters that characterize the interaction (like mass for gravity or the spring constant for a Hooke’s law force).
It is important to remember that potential energy is a property of the interactions between objects in a chosen system, and not just a property of each object. This is especially true for electric forces, although in the examples of potential energy we consider below, parts of the system are either so big (like Earth, compared to an object on its surface) or so small (like a massless spring), that the changes those parts undergo are negligible when included in the system.
Types of Potential Energy
For each type of interaction present in a system, you can label a corresponding type of potential energy. The total potential energy of the system is the sum of the potential energies of all the types. (This follows from the additive property of the dot product in the expression for the work done.) Let’s look at some specific examples of types of potential energy discussed in Work. First, we consider each of these forces when acting separately, and then when both act together.
Gravitational Potential Energy Near Earth's Surface
The system of interest consists of our planet, Earth, and one or more particles near its surface (or bodies small enough to be considered as particles, compared to Earth). The gravitational force on each particle (or body) is just its weight mg near the surface of Earth, acting vertically down. According to Newton’s third law, each particle exerts a force on Earth of equal magnitude but in the opposite direction. Newton’s second law tells us that the magnitude of the acceleration produced by each of these forces on Earth is mg divided by Earth’s mass. Since the ratio of the mass of any ordinary object to the mass of Earth is vanishingly small, the motion of Earth can be completely neglected. Therefore, we consider this system to be a group of single-particle systems, subject to the uniform gravitational force of Earth.
In Work, the work done on a body by Earth’s uniform gravitational force, near its surface, depended on the mass of the body, the acceleration due to gravity, and the difference in height the body traversed, as given by Equation 7.2.4. By definition, this work is the negative of the difference in the gravitational potential energy, so that difference is
ΔUgrav=−Wgrav,AB=mg(yB−yA).
You can see from this that the gravitational potential energy function, near Earth’s surface, is
U(y)=mgy+ const.
You can choose the value of the constant, as described in the discussion of Equation ???; however, for solving most problems, the most convenient constant to choose is zero for when y=0, which is the lowest vertical position in the problem.
The summit of Great Blue Hill in Milton, MA, is 147 m above its base and has an elevation above sea level of 195 m (Figure 8.2.2). (Its Native American name, Massachusett, was adopted by settlers for naming the Bay Colony and state near its location.) A 75-kg hiker ascends from the base to the summit. What is the gravitational potential energy of the hiker-Earth system with respect to zero gravitational potential energy at base height, when the hiker is (a) at the base of the hill, (b) at the summit, and (c) at sea level, afterward?
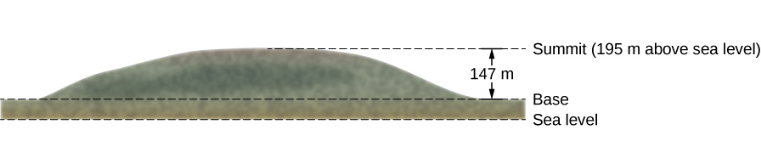
Strategy
First, we need to pick an origin for the y-axis and then determine the value of the constant that makes the potential energy zero at the height of the base. Then, we can determine the potential energies from Equation ???, based on the relationship between the zero potential energy height and the height at which the hiker is located.
Solution
a. Let’s choose the origin for the y-axis at base height, where we also want the zero of potential energy to be. This choice makes the constant equal to zero and
U( base )=U(0)=0
b. At the summit, y = 147 m, so
U( summit )=U(147m)=mgh=(75×9.8N)(147m)=108kJ.
c. At sea level, y = (147 - 195) m = -48 m, so
U (sea-level) =(75×9.8N)(−48m)=−35.3kJ.
Significance
Besides illustrating the use of Equation ??? and Equation ???, the values of gravitational potential energy we found are reasonable. The gravitational potential energy is higher at the summit than at the base, and lower at sea level than at the base. Gravity does work on you on your way up, too! It does negative work and not quite as much (in magnitude), as your muscles do. But it certainly does work. Similarly, your muscles do work on your way down, as negative work. The numerical values of the potential energies depend on the choice of zero of potential energy, but the physically meaningful differences of potential energy do not. [Note that since Equation ??? is a difference, the numerical values do not depend on the origin of coordinates.]
What are the values of the gravitational potential energy of the hiker at the base, summit, and sea level, with respect to a sea-level zero of potential energy?
Elastic Potential Energy
In Work, we saw that the work done by a perfectly elastic spring, in one dimension, depends only on the spring constant and the squares of the displacements from the unstretched position, as given in Equation 7.2.5. This work involves only the properties of a Hooke’s law interaction and not the properties of real springs and whatever objects are attached to them. Therefore, we can define the difference of elastic potential energy for a spring force as the negative of the work done by the spring force in this equation, before we consider systems that embody this type of force. Thus,
ΔU=−WAB=12k(x2B−x2A)
where the object travels from point A to point B. The potential energy function corresponding to this difference is
U(x)=12kx2+ const.
If the spring force is the only force acting, it is simplest to take the zero of potential energy at x = 0, when the spring is at its unstretched length. Then, the constant is Equation ??? is zero. (Other choices may be more convenient if other forces are acting.)
A system contains a perfectly elastic spring, with an unstretched length of 20 cm and a spring constant of 4 N/cm. (a) How much elastic potential energy does the spring contribute when its length is 23 cm? (b) How much more potential energy does it contribute if its length increases to 26 cm?
Strategy
When the spring is at its unstretched length, it contributes nothing to the potential energy of the system, so we can use Equation ??? with the constant equal to zero. The value of x is the length minus the unstretched length. When the spring is expanded, the spring’s displacement or difference between its relaxed length and stretched length should be used for the x-value in calculating the potential energy of the spring.
Solution
- The displacement of the spring is x = 23 cm − 20 cm = 3 cm, so the contributed potential energy is U = 12kx2 = 12(4 N/cm)(3 cm)2 = 0.18 J.
- When the spring’s displacement is x = 26 cm − 20 cm = 6 cm, the potential energy is U = 12kx2 = 12(4 N/cm)(6 cm)2 = 0.72 J, which is a 0.54-J increase over the amount in part (a).
Significance
Calculating the elastic potential energy and potential energy differences from Equation ??? involves solving for the potential energies based on the given lengths of the spring. Since U depends on x2, the potential energy for a compression (negative x) is the same as for an extension of equal magnitude.
When the length of the spring in Example 8.2.3 changes from an initial value of 22.0 cm to a final value, the elastic potential energy it contributes changes by −0.0800J. Find the final length.
Gravitational and Elastic Potential Energy
A simple system embodying both gravitational and elastic types of potential energy is a one-dimensional, vertical mass-spring system. This consists of a massive particle (or block), hung from one end of a perfectly elastic, massless spring, the other end of which is fixed, as illustrated in Figure 8.2.3.
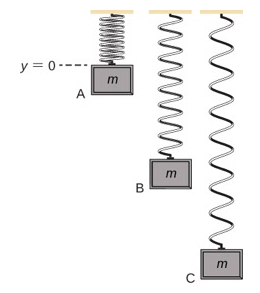
First, let's consider the potential energy of the system. We need to define the constant in the potential energy function of Equation ???. Often, the ground is a suitable choice for when the gravitational potential energy is zero; however, in this case, the highest point or when y = 0 is a convenient location for zero gravitational potential energy. Note that this choice is arbitrary, and the problem can be solved correctly even if another choice is picked.
We must also define the elastic potential energy of the system and the corresponding constant, as detailed in Equation ???. This is where the spring is unstretched, or at the y = 0 position.
If we consider that the total energy of the system is conserved, then the energy at point A equals point C. The block is placed just on the spring so its initial kinetic energy is zero. By the setup of the problem discussed previously, both the gravitational potential energy and elastic potential energy are equal to zero. Therefore, the initial energy of the system is zero. When the block arrives at point C, its kinetic energy is zero. However, it now has both gravitational potential energy and elastic potential energy. Therefore, we can solve for the distance y that the block travels before coming to a stop:
KA+UA=KC+UC0=0+mgyC+12k(yC)2yC=−2mgk

A block weighing 1.2 N is hung from a spring with a spring constant of 6.0 N/m, as shown in Figure 8.2.3. (a) What is the maximum expansion of the spring, as seen at point C? (b) What is the total potential energy at point B, halfway between A and C? (c) What is the speed of the block at point B?
Strategy
In part (a) we calculate the distance yC as discussed in the previous text. Then in part (b), we use half of the y value to calculate the potential energy at point B using equations Equation ??? and Equation ???. This energy must be equal to the kinetic energy, Equation 7.3.1, at point B since the initial energy of the system is zero. By calculating the kinetic energy at point B, we can now calculate the speed of the block at point B.
Solution
a. Since the total energy of the system is zero at point A as discussed previously, the maximum expansion of the spring is calculated to be:
yC=−2mgkyC=−2(1.2N)(6.0N/m)=−0.40m
b. The position of yB is half of the position at yC or -0.20 m. The total potential energy at point B would therefore be:
UB=mgyB+(12kyB)2UB=(1.2N)(−0.20m)+12(6N/m)(−0.20m)2UB=−0.12J
c. The mass of the block is the weight divided by gravity.
m=Fwg=1.2N9.8m/s2=0.12kg
The kinetic energy at point B therefore is 0.12 J because the total energy is zero. Therefore, the speed of the block at point B is equal to
K=12mv2v=√2Km=√2(0.12J)(0.12kg)=1.4m/s
Significance
Even though the potential energy due to gravity is relative to a chosen zero location, the solutions to this problem would be the same if the zero energy points were chosen at different locations.
Suppose the mass in Equation ??? is doubled while keeping the all other conditions the same. Would the maximum expansion of the spring increase, decrease, or remain the same? Would the speed at point B be larger, smaller, or the same compared to the original mass?
View this simulation to learn about conservation of energy with a skater! Build tracks, ramps and jumps for the skater and view the kinetic energy, potential energy and friction as he moves. You can also take the skater to different planets or even space!
A sample chart of a variety of energies is shown in Table 8.2.1 to give you an idea about typical energy values associated with certain events. Some of these are calculated using kinetic energy, whereas others are calculated by using quantities found in a form of potential energy that may not have been discussed at this point.
| Object/phenomenon | Energy in joules |
|---|---|
| Big Bang | 1068 |
| Annual world energy use | 4.0 x 1020 |
| Large fusion bomb (9 megaton) | 3.8 x 1016 |
| Hiroshima-size fission bomb (10 kiloton) | 4.2 x 1013 |
| 1 barrel crude oil | 5.9 x 109 |
| 1 ton TNT | 4.2 x 109 |
| 1 gallon of gasoline | 1.2 x 108 |
| Daily adult food intake (recommended) | 1.2 x 107 |
| 1000-kg car at 90 km/h | 3.1 x 105 |
| Tennis ball at 100 km/h | 22 |
| Mosquito (10−2 g at 0.5 m/s) | 1.3 x 10-6 |
| Single electron in a TV tube beam | 4.0 x 10-15 |
| Energy to break one DNA strand | 10-19 |


