10.5: Moment of Inertia and Rotational Kinetic Energy
( \newcommand{\kernel}{\mathrm{null}\,}\)
- Describe the differences between rotational and translational kinetic energy
- Define the physical concept of moment of inertia in terms of the mass distribution from the rotational axis
- Explain how the moment of inertia of rigid bodies affects their rotational kinetic energy
- Use conservation of mechanical energy to analyze systems undergoing both rotation and translation
- Calculate the angular velocity of a rotating system when there are energy losses due to nonconservative forces
So far in this chapter, we have been working with rotational kinematics: the description of motion for a rotating rigid body with a fixed axis of rotation. In this section, we define two new quantities that are helpful for analyzing properties of rotating objects: moment of inertia and rotational kinetic energy. With these properties defined, we will have two important tools we need for analyzing rotational dynamics.
Rotational Kinetic Energy
Any moving object has kinetic energy. We know how to calculate this for a body undergoing translational motion, but how about for a rigid body undergoing rotation? This might seem complicated because each point on the rigid body has a different velocity. However, we can make use of angular velocity—which is the same for the entire rigid body—to express the kinetic energy for a rotating object. Figure 10.5.1 shows an example of a very energetic rotating body: an electric grindstone propelled by a motor. Sparks are flying, and noise and vibration are generated as the grindstone does its work. This system has considerable energy, some of it in the form of heat, light, sound, and vibration. However, most of this energy is in the form of rotational kinetic energy.
Energy in rotational motion is not a new form of energy; rather, it is the energy associated with rotational motion, the same as kinetic energy in translational motion. However, because kinetic energy is given by K=12mv2, and velocity is a quantity that is different for every point on a rotating body about an axis, it makes sense to find a way to write kinetic energy in terms of the variable ω, which is the same for all points on a rigid rotating body. For a single particle rotating around a fixed axis, this is straightforward to calculate. We can relate the angular velocity to the magnitude of the translational velocity using the relation vt=ωr, where r is the distance of the particle from the axis of rotation and vt is its tangential speed. Substituting into the equation for kinetic energy, we find
K=12mv2t=12m(ωr)2=12(mr2)ω2.
In the case of a rigid rotating body, we can divide up any body into a large number of smaller masses, each with a mass mj and distance to the axis of rotation rj, such that the total mass of the body is equal to the sum of the individual masses: M=∑jmj. Each smaller mass has tangential speed vj, where we have dropped the subscript t for the moment. The total kinetic energy of the rigid rotating body is
K=∑j12mjv2j=∑j12mj(rjωj)2
and since ωj=ω for all masses,
K=12(∑jmjr2j)ω2.
The units of Equation ??? are joules (J). The equation in this form is complete, but awkward; we need to find a way to generalize it.
Moment of Inertia
If we compare Equation ??? to the way we wrote kinetic energy in Work and Kinetic Energy, (12mv2), this suggests we have a new rotational variable to add to our list of our relations between rotational and translational variables. The quantity ∑jmjr2j is the counterpart for mass in the equation for rotational kinetic energy. This is an important new term for rotational motion. This quantity is called the moment of inertia I, with units of kg·m2:
I=∑jmjr2j.
For now, we leave the expression in summation form, representing the moment of inertia of a system of point particles rotating about a fixed axis. We note that the moment of inertia of a single point particle about a fixed axis is simply mr2, with r being the distance from the point particle to the axis of rotation. In the next section, we explore the integral form of this equation, which can be used to calculate the moment of inertia of some regular-shaped rigid bodies.
The moment of inertia is the quantitative measure of rotational inertia, just as in translational motion, and mass is the quantitative measure of linear inertia—that is, the more massive an object is, the more inertia it has, and the greater is its resistance to change in linear velocity. Similarly, the greater the moment of inertia of a rigid body or system of particles, the greater is its resistance to change in angular velocity about a fixed axis of rotation. It is interesting to see how the moment of inertia varies with r, the distance to the axis of rotation of the mass particles in Equation ???. Rigid bodies and systems of particles with more mass concentrated at a greater distance from the axis of rotation have greater moments of inertia than bodies and systems of the same mass, but concentrated near the axis of rotation. In this way, we can see that a hollow cylinder has more rotational inertia than a solid cylinder of the same mass when rotating about an axis through the center. Substituting Equation ??? into Equation ???, the expression for the kinetic energy of a rotating rigid body becomes
K=12Iω2.
We see from this equation that the kinetic energy of a rotating rigid body is directly proportional to the moment of inertia and the square of the angular velocity. This is exploited in flywheel energy-storage devices, which are designed to store large amounts of rotational kinetic energy. Many carmakers are now testing flywheel energy storage devices in their automobiles, such as the flywheel, or kinetic energy recovery system, shown in Figure 10.5.2.

The rotational and translational quantities for kinetic energy and inertia are summarized in Table 10.4. The relationship column is not included because a constant doesn’t exist by which we could multiply the rotational quantity to get the translational quantity, as can be done for the variables in Table 10.3.
| Rotational | Translational |
|---|---|
| I=∑jmjr2j | m |
| K=12Iω2 | K=12mv2 |
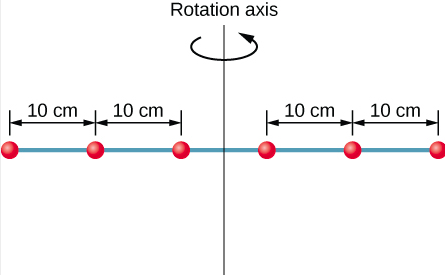
Six small washers are spaced 10 cm apart on a rod of negligible mass and 0.5 m in length. The mass of each washer is 20 g. The rod rotates about an axis located at 25 cm, as shown in Figure 10.5.3. (a) What is the moment of inertia of the system? (b) If the two washers closest to the axis are removed, what is the moment of inertia of the remaining four washers? (c) If the system with six washers rotates at 5 rev/s, what is its rotational kinetic energy?
Strategy
- We use the definition for moment of inertia for a system of particles and perform the summation to evaluate this quantity. The masses are all the same so we can pull that quantity in front of the summation symbol.
- We do a similar calculation.
- We insert the result from (a) into the expression for rotational kinetic energy.
Solution
- I=∑mjr2j=(0.02kg)(2×(0.25m)2+2×(0.15m)2+2×(0.05m)2)=0.0035kg⋅m2
- I=∑jmjr2j=(0.02kg)(2×(0.25m)2+2×(0.15m)2)=0.0034kg⋅m2
- K=12Iω2=12(0.0035kg⋅m2)(5.0×2πrad/s)2=1.73J
Significance
We can see the individual contributions to the moment of inertia. The masses close to the axis of rotation have a very small contribution. When we removed them, it had a very small effect on the moment of inertia.
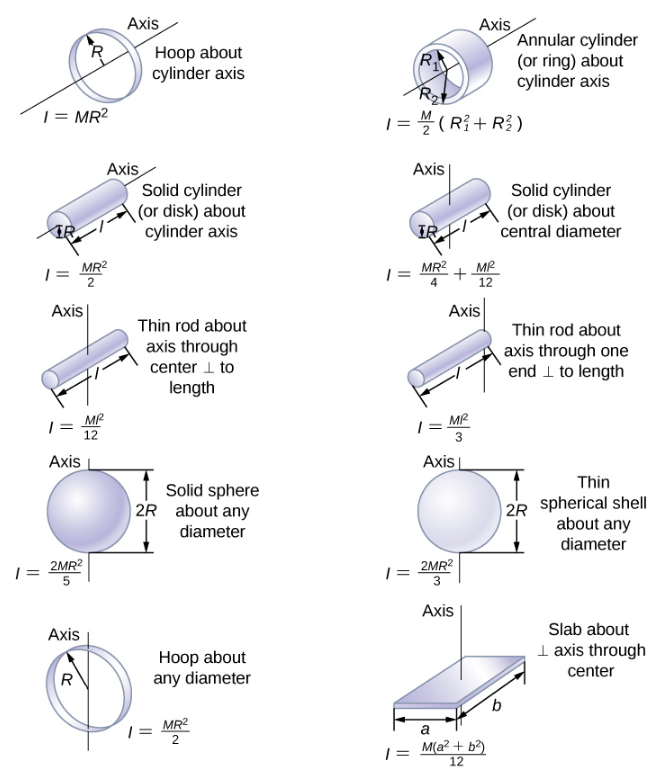
In the next section, we generalize the summation equation for point particles and develop a method to calculate moments of inertia for rigid bodies. For now, though, Figure 10.5.4 gives values of rotational inertia for common object shapes around specified axes.
Applying Rotational Kinetic Energy
Now let’s apply the ideas of rotational kinetic energy and the moment of inertia table to get a feeling for the energy associated with a few rotating objects. The following examples will also help get you comfortable using these equations. First, let’s look at a general problem-solving strategy for rotational energy.
- Determine that energy or work is involved in the rotation.
- Determine the system of interest. A sketch usually helps.
- Analyze the situation to determine the types of work and energy involved.
- If there are no losses of energy due to friction and other nonconservative forces, mechanical energy is conserved, that is, Ki+Ui=Kf+Uf.
- If nonconservative forces are present, mechanical energy is not conserved, and other forms of energy, such as heat and light, may enter or leave the system. Determine what they are and calculate them as necessary.
- Eliminate terms wherever possible to simplify the algebra.
- Evaluate the numerical solution to see if it makes sense in the physical situation presented in the wording of the problem.
A typical small rescue helicopter has four blades: Each is 4.00 m long and has a mass of 50.0 kg (Figure 10.5.5). The blades can be approximated as thin rods that rotate about one end of an axis perpendicular to their length. The helicopter has a total loaded mass of 1000 kg. (a) Calculate the rotational kinetic energy in the blades when they rotate at 300 rpm. (b) Calculate the translational kinetic energy of the helicopter when it flies at 20.0 m/s, and compare it with the rotational energy in the blades.

Strategy
Rotational and translational kinetic energies can be calculated from their definitions. The wording of the problem gives all the necessary constants to evaluate the expressions for the rotational and translational kinetic energies.
Solution
a. The rotational kinetic energy is
K=12Iω2
We must convert the angular velocity to radians per second and calculate the moment of inertia before we can find K. The angular velocity ω is
ω=300 rev 1.00min2π rad 1 rev 1.00min60.0s=31.4rads.
The moment of inertia of one blade is that of a thin rod rotated about its end, listed in Figure 10.5.4. The total I is four times this moment of inertia because there are four blades. Thus,
I=4Ml23=4×(50.0kg)(4.00m)23=1067.0kg⋅m2.
Entering ω and I into the expression for rotational kinetic energy gives
K=0.5(1067kg⋅m2)(31.4rad/s)2=5.26×105J.
b. Entering the given values into the equation for translational kinetic energy, we obtain
K=12mv2=(0.5)(1000.0kg)(20.0m/s)2=2.00×105J.
To compare kinetic energies, we take the ratio of translational kinetic energy to rotational kinetic energy. This ratio is
2.00×105J5.26×105J=0.380.
Significance
The ratio of translational energy to rotational kinetic energy is only 0.380. This ratio tells us that most of the kinetic energy of the helicopter is in its spinning blades.
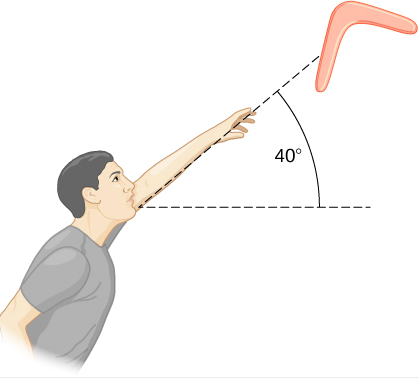
A person hurls a boomerang into the air with a velocity of 30.0 m/s at an angle of 40.0° with respect to the horizontal (Figure 10.5.6). It has a mass of 1.0 kg and is rotating at 10.0 rev/s. The moment of inertia of the boomerang is given as I=112mL2 where L = 0.7 m. (a) What is the total energy of the boomerang when it leaves the hand? (b) How high does the boomerang go from the elevation of the hand, neglecting air resistance?
Strategy
We use the definitions of rotational and linear kinetic energy to find the total energy of the system. The problem states to neglect air resistance, so we don’t have to worry about energy loss. In part (b), we use conservation of mechanical energy to find the maximum height of the boomerang.
Solution
a. Moment of inertia: I=112mL2=112(1.0kg)(0.7m)2=0.041kg⋅m2.
Angular Velocity: ω=(10.0rev/s)(2π)=62.83rad/s
The rotational kinetic energy is therefore
KR=12(0.041kg⋅m2)(62.83rad/s)2=80.93J
The translational kinetic energy is
KT=12mv2=12(1.0kg)(30.0m/s)2=450.0J
Thus, the total energy in the boomerang is
KTotal =KR+KT=80.93+450.0=530.93J.
b. We use conservation of mechanical energy. Since the boomerang is launched at an angle, we need to write the total energies of the system in terms of its linear kinetic energies using the velocity in the x- and y-directions. The total energy when the boomerang leaves the hand is
EBefore =12mv2x+12mv2y+12Iω2
The total energy at maximum height is
EFinal =12mv2x+12Iω2+mgh
By conservation of mechanical energy, EBefore=EFinal so we have, after canceling like terms,
12mv2y=mgh.
Since vy = 30.0 m/s (sin40∘) = 19.28 m/s, we find
h=(19.28m/s)22(9.8m/s2)=18.97m
Significance
In part (b), the solution demonstrates how energy conservation is an alternative method to solve a problem that normally would be solved using kinematics. In the absence of air resistance, the rotational kinetic energy was not a factor in the solution for the maximum height.
A nuclear submarine propeller has a moment of inertia of 800.0 kg • m2. If the submerged propeller has a rotation rate of 4.0 rev/s when the engine is cut, what is the rotation rate of the propeller after 5.0 s when water resistance has taken 50,000 J out of the system?


