14.4: Measuring Pressure
- Page ID
- 4056
- Define gauge pressure and absolute pressure
- Explain various methods for measuring pressure
- Understand the working of open-tube barometers
- Describe in detail how manometers and barometers operate
In the preceding section, we derived a formula for calculating the variation in pressure for a fluid in hydrostatic equilibrium. As it turns out, this is a very useful calculation. Measurements of pressure are important in daily life as well as in science and engineering applications. In this section, we discuss different ways that pressure can be reported and measured.
Gauge Pressure vs. Absolute Pressure
Suppose the pressure gauge on a full scuba tank reads 3000 psi, which is approximately 207 atmospheres. When the valve is opened, air begins to escape because the pressure inside the tank is greater than the atmospheric pressure outside the tank. Air continues to escape from the tank until the pressure inside the tank equals the pressure of the atmosphere outside the tank. At this point, the pressure gauge on the tank reads zero, even though the pressure inside the tank is actually 1 atmosphere—the same as the air pressure outside the tank.
Most pressure gauges, like the one on the scuba tank, are calibrated to read zero at atmospheric pressure. Pressure readings from such gauges are called gauge pressure, which is the pressure relative to the atmospheric pressure. When the pressure inside the tank is greater than atmospheric pressure, the gauge reports a positive value. Some gauges are designed to measure negative pressure. For example, many physics experiments must take place in a vacuum chamber, a rigid chamber from which some of the air is pumped out. The pressure inside the vacuum chamber is less than atmospheric pressure, so the pressure gauge on the chamber reads a negative value. Unlike gauge pressure, absolute pressure accounts for atmospheric pressure, which in effect adds to the pressure in any fluid not enclosed in a rigid container.
The absolute pressure, or total pressure, is the sum of gauge pressure and atmospheric pressure:
\[p_{abs} = p_{g} + p_{atm} \label{14.11}\]
where pabsis absolute pressure, pg is gauge pressure, and patm is atmospheric pressure.
For example, if a tire gauge reads 34 psi, then the absolute pressure is 34 psi plus 14.7 psi (patm in psi), or 48.7 psi (equivalent to 336 kPa).
In most cases, the absolute pressure in fluids cannot be negative. Fluids push rather than pull, so the smallest absolute pressure in a fluid is zero (a negative absolute pressure is a pull). Thus, the smallest possible gauge pressure is pg = −patm (which makes pabs zero). There is no theoretical limit to how large a gauge pressure can be.
Measuring Pressure
A host of devices are used for measuring pressure, ranging from tire gauges to blood pressure monitors. Many other types of pressure gauges are commonly used to test the pressure of fluids, such as mechanical pressure gauges. We will explore some of these in this section.
Any property that changes with pressure in a known way can be used to construct a pressure gauge. Some of the most common types include strain gauges, which use the change in the shape of a material with pressure; capacitance pressure gauges, which use the change in electric capacitance due to shape change with pressure; piezoelectric pressure gauges, which generate a voltage difference across a piezoelectric material under a pressure difference between the two sides; and ion gauges, which measure pressure by ionizing molecules in highly evacuated chambers. Different pressure gauges are useful in different pressure ranges and under different physical situations. Some examples are shown in Figure \(\PageIndex{1}\).

Manometers
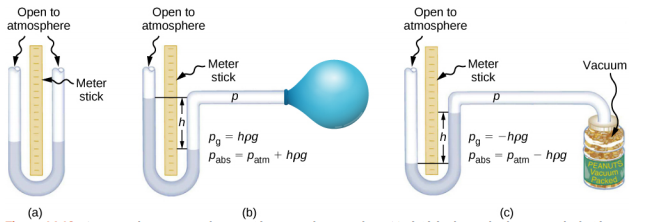
One of the most important classes of pressure gauges applies the property that pressure due to the weight of a fluid of constant density is given by p = h\(\rho\)g. The U-shaped tube shown in Figure \(\PageIndex{2}\) is an example of a manometer; in part (a), both sides of the tube are open to the atmosphere, allowing atmospheric pressure to push down on each side equally so that its effects cancel.
A manometer with only one side open to the atmosphere is an ideal device for measuring gauge pressures. The gauge pressure is pg = h\(\rho\)g and is found by measuring h. For example, suppose one side of the U-tube is connected to some source of pressure pabs, such as the balloon in part (b) of the figure or the vacuum-packed peanut jar shown in part (c). Pressure is transmitted undiminished to the manometer, and the fluid levels are no longer equal. In part (b), pabs is greater than atmospheric pressure, whereas in part (c), pabs is less than atmospheric pressure. In both cases, pabs differs from atmospheric pressure by an amount h\(\rho\)g, where \(\rho\) is the density of the fluid in the manometer. In part (b), pabs can support a column of fluid of height h, so it must exert a pressure h\(\rho\)g greater than atmospheric pressure (the gauge pressure pg is positive). In part (c), atmospheric pressure can support a column of fluid of height h, so pabsis less than atmospheric pressure by an amount h\(\rho\)g (the gauge pressure pg is negative).
Barometers
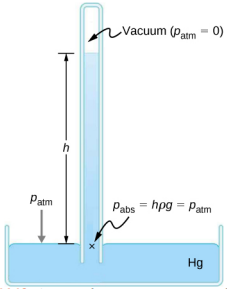
Manometers typically use a U-shaped tube of a fluid (often mercury) to measure pressure. A barometer (Figure \(\PageIndex{3}\)) is a device that typically uses a single column of mercury to measure atmospheric pressure. The barometer, invented by the Italian mathematician and physicist Evangelista Torricelli (1608–1647) in 1643, is constructed from a glass tube closed at one end and filled with mercury. The tube is then inverted and placed in a pool of mercury. This device measures atmospheric pressure, rather than gauge pressure, because there is a nearly pure vacuum above the mercury in the tube. The height of the mercury is such that h\(\rho\)g = patm. When atmospheric pressure varies, the mercury rises or falls.
Weather forecasters closely monitor changes in atmospheric pressure (often reported as barometric pressure), as rising mercury typically signals improving weather and falling mercury indicates deteriorating weather. The barometer can also be used as an altimeter, since average atmospheric pressure varies with altitude. Mercury barometers and manometers are so common that units of mm Hg are often quoted for atmospheric pressure and blood pressures.
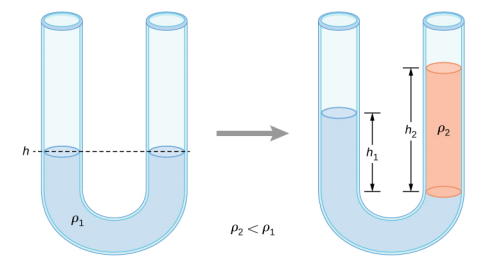
A U-tube with both ends open is filled with a liquid of density \(\rho_{1}\) to a height h on both sides (Figure \(\PageIndex{1}\)). A liquid of density \(\rho_{2} < \rho_{1}\) is poured into one side and Liquid 2 settles on top of Liquid 1. The heights on the two sides are different. The height to the top of Liquid 2 from the interface is h2 and the height to the top of Liquid 1 from the level of the interface is h1. Derive a formula for the height difference.
Strategy
The pressure at points at the same height on the two sides of a U-tube must be the same as long as the two points are in the same liquid. Therefore, we consider two points at the same level in the two arms of the tube: One point is the interface on the side of the Liquid 2 and the other is a point in the arm with Liquid 1 that is at the same level as the interface in the other arm. The pressure at each point is due to atmospheric pressure plus the weight of the liquid above it.
Pressure on the side with Liquid 1 = p0 + \(\rho_{1}\) gh1
Pressure on the side with Liquid 2 = p0 + \(\rho_{2}\) gh2
Solution
Since the two points are in Liquid 1 and are at the same height, the pressure at the two points must be the same. Therefore, we have
\[p_{0} + \rho_{1} gh_{1} = p_{0} + \rho_{2} gh_{2} \ldotp \nonumber\]
Hence,
\[\rho_{1} h_{1} = \rho_{2} h_{2} \ldotp \nonumber\]
This means that the difference in heights on the two sides of the U-tube is
\[h_{2} - h_{1} = \left(1 - \dfrac{p_{1}}{p_{2}}\right) h_{2} \ldotp \nonumber\]
The result makes sense if we set \(\rho_2 = \rho_1\), which gives h2 = h1. If the two sides have the same density, they have the same height.
Mercury is a hazardous substance. Why do you suppose mercury is typically used in barometers instead of a safer fluid such as water?
Units of pressure
As stated earlier, the SI unit for pressure is the pascal (Pa), where
\[1\; Pa = 1\; N/m^{2} \ldotp\]
In addition to the pascal, many other units for pressure are in common use (Table \(\PageIndex{1}\)). In meteorology, atmospheric pressure is often described in the unit of millibars (mb), where
\[1000\; mb = 1 \times 10^{5}\; Pa \ldotp\]
The millibar is a convenient unit for meteorologists because the average atmospheric pressure at sea level on Earth is 1.013 x 105 Pa = 1013 mb = 1 atm. Using the equations derived when considering pressure at a depth in a fluid, pressure can also be measured as millimeters or inches of mercury. The pressure at the bottom of a 760-mm column of mercury at 0 °C in a container where the top part is evacuated is equal to the atmospheric pressure. Thus, 760 mm Hg is also used in place of 1 atmosphere of pressure. In vacuum physics labs, scientists often use another unit called the torr, named after Torricelli, who, as we have just seen, invented the mercury manometer for measuring pressure. One torr is equal to a pressure of 1 mm Hg.
| Unit | Definition |
|---|---|
| SI unit: the Pascal | $$1\; Pa = 1\; N/m^{2}$$ |
| English unit: pounds per square inch ( lb/in.2 or psi) | $$1\; psi = 7.015 \times 10^{3}\; Pa$$ |
| Other units of pressure | $$\begin{split} 1\; atm & = 760\; mm\; Hg \\ & = 1.013 \times 10^{5}\; Pa \\ & = 14.7\; psi \\ & = 29.9\; inches\; of\; Hg \\ & = 1013\; mb \end{split}$$ |
| $$1\; bar = 10^{5}\; Pa$$ | |
| $$1\; torr = 1\; mm\; Hg = 122.39\; Pa$$ |


