17.2: Sound Waves
( \newcommand{\kernel}{\mathrm{null}\,}\)
- Explain the difference between sound and hearing
- Describe sound as a wave
- List the equations used to model sound waves
- Describe compression and rarefactions as they relate to sound
The physical phenomenon of sound is a disturbance of matter that is transmitted from its source outward. Hearing is the perception of sound, just as seeing is the perception of visible light. On the atomic scale, sound is a disturbance of atoms that is far more ordered than their thermal motions. In many instances, sound is a periodic wave, and the atoms undergo simple harmonic motion. Thus, sound waves can induce oscillations and resonance effects (Figure 17.2.2).
This video shows waves on the surface of a wine glass, being driven by sound waves from a speaker. As the frequency of the sound wave approaches the resonant frequency of the wine glass, the amplitude and frequency of the waves on the wine glass increase. When the resonant frequency is reached, the glass shatters.
Video 17.2.1: Breaking a wine glass using resonance by playing sound at its resonance frequency. https://www.youtube.com/watch?v=17tqXgvCN0E
A speaker produces a sound wave by oscillating a cone, causing vibrations of air molecules. In Figure 17.2.2, a speaker vibrates at a constant frequency and amplitude, producing vibrations in the surrounding air molecules. As the speaker oscillates back and forth, it transfers energy to the air, mostly as thermal energy. But a small part of the speaker’s energy goes into compressing and expanding the surrounding air, creating slightly higher and lower local pressures. These compressions (high-pressure regions) and rarefactions (low-pressure regions) move out as longitudinal pressure waves having the same frequency as the speaker—they are the disturbance that is a sound wave. (Sound waves in air and most fluids are longitudinal, because fluids have almost no shear strength. In solids, sound waves can be both transverse and longitudinal.)
Figure 17.2.2a shows the compressions and rarefactions, and also shows a graph of gauge pressure versus distance from a speaker. As the speaker moves in the positive x-direction, it pushes air molecules, displacing them from their equilibrium positions. As the speaker moves in the negative x-direction, the air molecules move back toward their equilibrium positions due to a restoring force. The air molecules oscillate in simple harmonic motion about their equilibrium positions, as shown Figure 17.2.2b. Note that sound waves in air are longitudinal, and in the figure, the wave propagates in the positive x-direction and the molecules oscillate parallel to the direction in which the wave propagates.
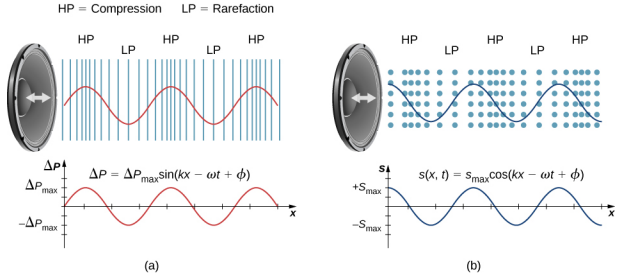
Sound can be modeled as a pressure wave by considering the change in pressure from average pressure,
ΔP=ΔPmaxsin(kx∓ωt+ϕ).
This equation is similar to the periodic wave equations seen in Waves, where ΔP is the change in pressure, ΔPmax is the maximum change in pressure, k=2πλ is the wave number, ω=2πT=2πf is the angular frequency, and ϕ is the initial phase. The wave speed can be determined from
v=ωk=λT.
Sound waves can also be modeled in terms of the displacement of the air molecules. The displacement of the air molecules can be modeled using a cosine function:
s(x,t)=smaxcos(kx∓ωt+ϕ).
In this equation, s is the displacement and smax is the maximum displacement.
Not shown in the figure is the amplitude of a sound wave as it decreases with distance from its source, because the energy of the wave is spread over a larger and larger area. The intensity decreases as it moves away from the speaker, as discussed in Waves. The energy is also absorbed by objects and converted into thermal energy by the viscosity of the air. In addition, during each compression, a little heat transfers to the air; during each rarefaction, even less heat transfers from the air, and these heat transfers reduce the organized disturbance into random thermal motions. Whether the heat transfer from compression to rarefaction is significant depends on how far apart they are—that is, it depends on wavelength. Wavelength, frequency, amplitude, and speed of propagation are important characteristics for sound, as they are for all waves.



