17.8: The Doppler Effect
( \newcommand{\kernel}{\mathrm{null}\,}\)
- Explain the change in observed frequency as a moving source of sound approaches or departs from a stationary observer
- Explain the change in observed frequency as an observer moves toward or away from a stationary source of sound
The characteristic sound of a motorcycle buzzing by is an example of the Doppler effect. Specifically, if you are standing on a street corner and observe an ambulance with a siren sounding passing at a constant speed, you notice two characteristic changes in the sound of the siren. First, the sound increases in loudness as the ambulance approaches and decreases in loudness as it moves away, which is expected. But in addition, the high-pitched siren shifts dramatically to a lower-pitched sound. As the ambulance passes, the frequency of the sound heard by a stationary observer changes from a constant high frequency to a constant lower frequency, even though the siren is producing a constant source frequency. The closer the ambulance brushes by, the more abrupt the shift. Also, the faster the ambulance moves, the greater the shift. We also hear this characteristic shift in frequency for passing cars, airplanes, and trains.
The Doppler effect is an alteration in the observed frequency of a sound due to motion of either the source or the observer. Although less familiar, this effect is easily noticed for a stationary source and moving observer. For example, if you ride a train past a stationary warning horn, you will hear the horn’s frequency shift from high to low as you pass by. The actual change in frequency due to relative motion of source and observer is called a Doppler shift. The Doppler effect and Doppler shift are named for the Austrian physicist and mathematician Christian Johann Doppler (1803–1853), who did experiments with both moving sources and moving observers. Doppler, for example, had musicians play on a moving open train car and also play standing next to the train tracks as a train passed by. Their music was observed both on and off the train, and changes in frequency were measured.
What causes the Doppler shift? Figure 17.8.1 illustrates sound waves emitted by stationary and moving sources in a stationary air mass. Each disturbance spreads out spherically from the point at which the sound is emitted. If the source is stationary, then all of the spheres representing the air compressions in the sound wave are centered on the same point, and the stationary observers on either side hear the same wavelength and frequency as emitted by the source (case a). If the source is moving, the situation is different. Each compression of the air moves out in a sphere from the point at which it was emitted, but the point of emission moves. This moving emission point causes the air compressions to be closer together on one side and farther apart on the other. Thus, the wavelength is shorter in the direction the source is moving (on the right in case b), and longer in the opposite direction (on the left in case b). Finally, if the observers move, as in case (c), the frequency at which they receive the compressions changes. The observer moving toward the source receives them at a higher frequency, and the person moving away from the source receives them at a lower frequency.
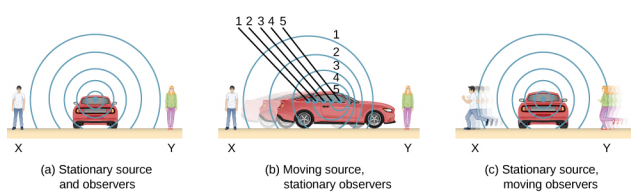
We know that wavelength and frequency are related by v = fλ, where v is the fixed speed of sound. The sound moves in a medium and has the same speed v in that medium whether the source is moving or not. Thus, f multiplied by λ is a constant. Because the observer on the right in case (b) receives a shorter wavelength, the frequency she receives must be higher. Similarly, the observer on the left receives a longer wavelength, and hence he hears a lower frequency. The same thing happens in case (c). A higher frequency is received by the observer moving toward the source, and a lower frequency is received by an observer moving away from the source. In general, then, relative motion of source and observer toward one another increases the received frequency. Relative motion apart decreases frequency. The greater the relative speed, the greater the effect.
The Doppler effect occurs not only for sound, but for any wave when there is relative motion between the observer and the source. Doppler shifts occur in the frequency of sound, light, and water waves, for example. Doppler shifts can be used to determine velocity, such as when ultrasound is reflected from blood in a medical diagnostic. The relative velocities of stars and galaxies is determined by the shift in the frequencies of light received from them and has implied much about the origins of the universe. Modern physics has been profoundly affected by observations of Doppler shifts.
Derivation of the Observed Frequency due to the Doppler Shift
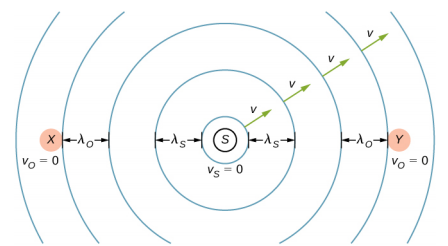
Consider two stationary observers X and Y in Figure 17.8.2, located on either side of a stationary source. Each observer hears the same frequency, and that frequency is the frequency produced by the stationary source.
Now consider a stationary observer X with a source moving away from the observer with a constant speed vs < v (Figure 17.8.3). At time t = 0 , the source sends out a sound wave, indicated in black. This wave moves out at the speed of sound v. The position of the sound wave at each time interval of period Ts is shown as dotted lines. After one period, the source has moved Δx = vsTs and emits a second sound wave, which moves out at the speed of sound. The source continues to move and produce sound waves, as indicated by the circles numbered 3 and 4. Notice that as the waves move out, they remained centered at their respective point of origin.
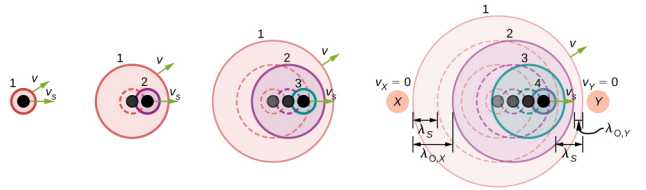
Using the fact that the wavelength is equal to the speed times the period, and the period is the inverse of the frequency, we can derive the observed frequency:
λo=λs+ΔxvTo=vTs+vsTsvfo=vfs+vsfs=v+vsfsfo=fs(vv+vs).
As the source moves away from the observer, the observed frequency is lower than the source frequency.
Now consider a source moving at a constant velocity vs, moving toward a stationary observer Y, also shown in Figure 17.8.3. The wavelength is observed by Y as λo=λs−Δx=λs−vsTs. Once again, using the fact that the wavelength is equal to the speed times the period, and the period is the inverse of the frequency, we can derive the observed frequency:
λo=λs−ΔxvTo=vTs−vsTsvfo=vfs−vsfs=v−vsfsfo=fs(vv−vs).
When a source is moving and the observer is stationary, the observed frequency is
fo=fs(vv∓vs),
where fo is the frequency observed by the stationary observer, fs is the frequency produced by the moving source, v is the speed of sound, vs is the constant speed of the source, and the top sign is for the source approaching the observer and the bottom sign is for the source departing from the observer.
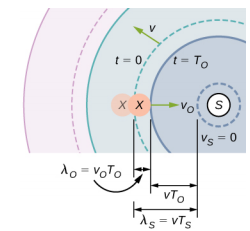
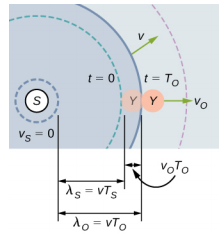
What happens if the observer is moving and the source is stationary? If the observer moves toward the stationary source, the observed frequency is higher than the source frequency. If the observer is moving away from the stationary source, the observed frequency is lower than the source frequency. Consider observer X in Figure 17.8.4 as the observer moves toward a stationary source with a speed vo. The source emits a tone with a constant frequency fs and constant period Ts. The observer hears the first wave emitted by the source. If the observer were stationary, the time for one wavelength of sound to pass should be equal to the period of the source Ts. Since the observer is moving toward the source, the time for one wavelength to pass is less than Ts and is equal to the observed period To = Ts − Δt. At time t = 0, the observer starts at the beginning of a wavelength and moves toward the second wavelength as the wavelength moves out from the source. The wavelength is equal to the distance the observer traveled plus the distance the sound wave traveled until it is met by the observer:
λs=vTo+voTovTs=(v+vo)Tov(1fs)=(v+vo)(1fo)fo=fs(v+vov).
If the observer is moving away from the source (Figure 17.8.5), the observed frequency can be found:
λs=vTo−voTovTs=(v−vo)Tov(1fs)=(v−vo)(1fo)fo=fs(v−vov).
The equations for an observer moving toward or away from a stationary source can be combined into one equation:
fo=fs(v±vov),
where fo is the observed frequency, fs is the source frequency, v is the speed of sound, vo is the speed of the observer, the top sign is for the observer approaching the source and the bottom sign is for the observer departing from the source. Equation ??? and Equation ??? can be summarized in one equation (the top sign is for approaching) and is further illustrated in Table 17.8.1, where fo is the observed frequency, fs is the source frequency, v is the speed of sound, vo is the speed of the observer, vs is the speed of the source, the top sign is for approaching and the bottom sign is for departing.
fo=fs(v±vov∓vs),
| Doppler shift fo=fs(v±vov∓vs) | Stationary observer | Observer moving towards source | Observer moving away from source |
|---|---|---|---|
| Stationary source | fo=fs |
fo=fs(v+vov) |
fo=fs(v−vov) |
| Source moving towards observer | fo=fs(vv−vs) |
fo=fs(v+vov−vs) |
fo=fs(v−vov−vs) |
| Source moving away from observer | fo=fs(vv+vs) |
fo=fs(v+vov+vs) |
fo=fs(v−vov+vs) |
The Doppler effect involves motion and this video will help visualize the effects of a moving observer or source. The video shows a moving source and a stationary observer, and a moving observer and a stationary source. It also discusses the Doppler effect and its application to light.
Suppose a train that has a 150-Hz horn is moving at 35.0 m/s in still air on a day when the speed of sound is 340 m/s.
- What frequencies are observed by a stationary person at the side of the tracks as the train approaches and after it passes?
- What frequency is observed by the train’s engineer traveling on the train?
Strategy
To find the observed frequency in (a), we must use fobs = fs(vv∓vs) because the source is moving. The minus sign is used for the approaching train, and the plus sign for the receding train. In (b), there are two Doppler shifts—one for a moving source and the other for a moving observer.
Solution
- Enter known values into fo = fs(vv−vs): fo=fs(vv−vs)=(150Hz)(340m/s340m/s−35.0m/s).Calculate the frequency observed by a stationary person as the train approaches: fo=(150Hz)(1.11)=167Hz.Use the same equation with the plus sign to find the frequency heard by a stationary person as the train recedes: fo=fs(vv+vs)=(150Hz)(340m/s340m/s+35.0m/s).Calculate the second frequency: fo=(150Hz)(0.907)=136Hz.
- Identify knowns:
- It seems reasonable that the engineer would receive the same frequency as emitted by the horn, because the relative velocity between them is zero.
- Relative to the medium (air), the speeds are vs = vo = 35.0 m/s.
- The first Doppler shift is for the moving observer; the second is for the moving source.
Use the following equation:
fo=[fs(v±vov)](vv∓vs).
The quantity in the square brackets is the Doppler-shifted frequency due to a moving observer. The factor on the right is the effect of the moving source. Because the train engineer is moving in the direction toward the horn, we must use the plus sign for vobs; however, because the horn is also moving in the direction away from the engineer, we also use the plus sign for vs. But the train is carrying both the engineer and the horn at the same velocity, so vs = vo. As a result, everything but fs cancels, yielding
fo=fs.
Significance
For the case where the source and the observer are not moving together, the numbers calculated are valid when the source (in this case, the train) is far enough away that the motion is nearly along the line joining source and observer. In both cases, the shift is significant and easily noticed. Note that the shift is 17.0 Hz for motion toward and 14.0 Hz for motion away. The shifts are not symmetric.
For the engineer riding in the train, we may expect that there is no change in frequency because the source and observer move together. This matches your experience. For example, there is no Doppler shift in the frequency of conversations between driver and passenger on a motorcycle. People talking when a wind moves the air between them also observe no Doppler shift in their conversation. The crucial point is that source and observer are not moving relative to each other.
Describe a situation in your life when you might rely on the Doppler shift to help you either while driving a car or walking near traffic.
The Doppler effect and the Doppler shift have many important applications in science and engineering. For example, the Doppler shift in ultrasound can be used to measure blood velocity, and police use the Doppler shift in radar (a microwave) to measure car velocities. In meteorology, the Doppler shift is used to track the motion of storm clouds; such “Doppler Radar” can give the velocity and direction of rain or snow in weather fronts. In astronomy, we can examine the light emitted from distant galaxies and determine their speed relative to ours. As galaxies move away from us, their light is shifted to a lower frequency, and so to a longer wavelength—the so-called red shift. Such information from galaxies far, far away has allowed us to estimate the age of the universe (from the Big Bang) as about 14 billion years.


