26: Vision and Optical Instruments (Exercises)
- Page ID
- 4210
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Conceptual Questions
26.1: Physics of the Eye
1. If the lens of a person’s eye is removed because of cataracts (as has been done since ancient times), why would you expect a spectacle lens of about 16 D to be prescribed?
2. A cataract is cloudiness in the lens of the eye. Is light dispersed or diffused by it?
3. When laser light is shone into a relaxed normal-vision eye to repair a tear by spot-welding the retina to the back of the eye, the rays entering the eye must be parallel. Why?
4. How does the power of a dry contact lens compare with its power when resting on the tear layer of the eye? Explain.
5. Why is your vision so blurry when you open your eyes while swimming under water? How does a face mask enable clear vision?
26.2: Vision Correction
6. It has become common to replace the cataract-clouded lens of the eye with an internal lens. This intraocular lens can be chosen so that the person has perfect distant vision. Will the person be able to read without glasses? If the person was nearsighted, is the power of the intraocular lens greater or less than the removed lens?
7. If the cornea is to be reshaped (this can be done surgically or with contact lenses) to correct myopia, should its curvature be made greater or smaller? Explain. Also explain how hyperopia can be corrected.
8. If there is a fixed percent uncertainty in LASIK reshaping of the cornea, why would you expect those people with the greatest correction to have a poorer chance of normal distant vision after the procedure?
9. A person with presbyopia has lost some or all of the ability to accommodate the power of the eye. If such a person’s distant vision is corrected with LASIK, will she still need reading glasses? Explain.
26.3: Color and Color Vision
10. A pure red object on a black background seems to disappear when illuminated with pure green light. Explain why.
11. What is color constancy, and what are its limitations?
12. There are different types of color blindness related to the malfunction of different types of cones. Why would it be particularly useful to study those rare individuals who are color blind only in one eye or who have a different type of color blindness in each eye?
13. Propose a way to study the function of the rods alone, given they can sense light about 1000 times dimmer than the cones.
26.4: Microscopes
14. Geometric optics describes the interaction of light with macroscopic objects. Why, then, is it correct to use geometric optics to analyse a microscope’s image?
15. The image produced by the microscope in Figure cannot be projected. Could extra lenses or mirrors project it? Explain.
16. Why not have the objective of a microscope form a case 2 image with a large magnification? (Hint: Consider the location of that image and the difficulty that would pose for using the eyepiece as a magnifier.)
17. What advantages do oil immersion objectives offer?
18. How does the \(\displaystyle NA\) of a microscope compare with the \(\displaystyle NA\) of an optical fiber?
26.5: Telescopes
19. If you want your microscope or telescope to project a real image onto a screen, how would you change the placement of the eyepiece relative to the objective?
26.6: Aberrations
20. List the various types of aberrations. What causes them and how can each be reduced?
Problem & Exercises
26.1: Physics of the Eye
Unless otherwise stated, the lens-to-retina distance is 2.00 cm.
21. What is the power of the eye when viewing an object 50.0 cm away?
Solution
52.0 D
22. Calculate the power of the eye when viewing an object 3.00 m away.
(a) The print in many books averages 3.50 mm in height. How high is the image of the print on the retina when the book is held 30.0 cm from the eye?
(b) Compare the size of the print to the sizes of rods and cones in the fovea and discuss the possible details observable in the letters. (The eye-brain system can perform better because of interconnections and higher order image processing.)
Solution
(a) −0.233 mm
(b) The size of the rods and the cones is smaller than the image height, so we can distinguish letters on a page.
23. Suppose a certain person’s visual acuity is such that he can see objects clearly that form an image 4.00 μm high on his retina. What is the maximum distance at which he can read the 75.0 cm high letters on the side of an airplane?
24. People who do very detailed work close up, such as jewellers, often can see objects clearly at much closer distance than the normal 25 cm.
(a) What is the power of the eyes of a woman who can see an object clearly at a distance of only 8.00 cm?
(b) What is the size of an image of a 1.00 mm object, such as lettering inside a ring, held at this distance?
(c) What would the size of the image be if the object were held at the normal 25.0 cm distance?
Solution
(a) +62.5 D
(b) –0.250 mm
(c) –0.0800 mm
26.2: Vision Correction
25. What is the far point of a person whose eyes have a relaxed power of 50.5 D?
Solution
2.00 m
26. What is the near point of a person whose eyes have an accommodated power of 53.5 D?
27. (a) A laser vision correction reshaping the cornea of a myopic patient reduces the power of his eye by 9.00 D, with a \(\displaystyle ±5.0%\) uncertainty in the final correction. What is the range of diopters for spectacle lenses that this person might need after LASIK procedure?
(b) Was the person nearsighted or farsighted before the procedure? How do you know?
Solution
(a) ±0.45 D
(b) The person was nearsighted because the patient was myopic and the power was reduced.
28. In a LASIK vision correction, the power of a patient’s eye is increased by 3.00 D. Assuming this produces normal close vision, what was the patient’s near point before the procedure?
29. What was the previous far point of a patient who had laser vision correction that reduced the power of her eye by 7.00 D, producing normal distant vision for her?
Solution
0.143 m
30. A severely myopic patient has a far point of 5.00 cm. By how many diopters should the power of his eye be reduced in laser vision correction to obtain normal distant vision for him?
31. A student’s eyes, while reading the blackboard, have a power of 51.0 D. How far is the board from his eyes?
Solution
1.00 m
32. The power of a physician’s eyes is 53.0 D while examining a patient. How far from her eyes is the feature being examined?
33. A young woman with normal distant vision has a 10.0% ability to accommodate (that is, increase) the power of her eyes. What is the closest object she can see clearly?
Solution
20.0 cm
34. The far point of a myopic administrator is 50.0 cm. (a) What is the relaxed power of his eyes? (b) If he has the normal 8.00% ability to accommodate, what is the closest object he can see clearly?
35. A very myopic man has a far point of 20.0 cm. What power contact lens (when on the eye) will correct his distant vision?
Solution
–5.00 D
36. Repeat the previous problem for eyeglasses held 1.50 cm from the eyes.
37. A myopic person sees that her contact lens prescription is –4.00 D. What is her far point?
Solution
25.0 cm
38. Repeat the previous problem for glasses that are 1.75 cm from the eyes.
39. The contact lens prescription for a mildly farsighted person is 0.750 D, and the person has a near point of 29.0 cm. What is the power of the tear layer between the cornea and the lens if the correction is ideal, taking the tear layer into account?
Solution
–0.198 D
40. A nearsighted man cannot see objects clearly beyond 20 cm from his eyes. How close must he stand to a mirror in order to see what he is doing when he shaves?
41. A mother sees that her child’s contact lens prescription is 0.750 D. What is the child’s near point?
Solution
30.8 cm
42. Repeat the previous problem for glasses that are 2.20 cm from the eyes.
43. The contact lens prescription for a nearsighted person is \(\displaystyle –4.00 D\) and the person has a far point of 22.5 cm. What is the power of the tear layer between the cornea and the lens if the correction is ideal, taking the tear layer into account?
Solution
–0.444 D
44. Unreasonable Results
A boy has a near point of 50 cm and a far point of 500 cm. Will a \(\displaystyle –4.00 D\) lens correct his far point to infinity?
26.4: Microscopes
45. A microscope with an overall magnification of 800 has an objective that magnifies by 200.
(a) What is the magnification of the eyepiece?
(b) If there are two other objectives that can be used, having magnifications of 100 and 400, what other total magnifications are possible?
Solution
(a) 4.00
(b) 1600
46. (a) What magnification is produced by a 0.150 cm focal length microscope objective that is 0.155 cm from the object being viewed?
(b) What is the overall magnification if an 8× eyepiece (one that produces a magnification of 8.00) is used?
47. (a) Where does an object need to be placed relative to a microscope for its 0.500 cm focal length objective to produce a magnification of \(\displaystyle –400\)?
(b) Where should the 5.00 cm focal length eyepiece be placed to produce a further fourfold (4.00) magnification?
Solution
(a) 0.501 cm
(b) Eyepiece should be 204 cm behind the objective lens.
48. You switch from a \(\displaystyle 1.40NA60×\) oil immersion objective to a \(\displaystyle 1.40NA60×\) oil immersion objective. What are the acceptance angles for each? Compare and comment on the values. Which would you use first to locate the target area on your specimen?
49. An amoeba is 0.305 cm away from the 0.300 cm focal length objective lens of a microscope.
(a) Where is the image formed by the objective lens?
(b) What is this image’s magnification?
(c) An eyepiece with a 2.00 cm focal length is placed 20.0 cm from the objective. Where is the final image?
(d) What magnification is produced by the eyepiece?
(e) What is the overall magnification? (See Figure.)
Solution
(a) +18.3 cm (on the eyepiece side of the objective lens)
(b) -60.0
(c) -11.3 cm (on the objective side of the eyepiece)
(d) +6.67
(e) -400
50. You are using a standard microscope with a \(\displaystyle 0.10NA4×\) objective and switch to a \(\displaystyle 0.65NA40×\) objective. What are the acceptance angles for each? Compare and comment on the values. Which would you use first to locate the target area on of your specimen? (See Figure.)
51. Unreasonable Results
Your friends show you an image through a microscope. They tell you that the microscope has an objective with a 0.500 cm focal length and an eyepiece with a 5.00 cm focal length. The resulting overall magnification is 250,000. Are these viable values for a microscope?
26.5: Telescopes
Unless otherwise stated, the lens-to-retina distance is 2.00 cm.
52. What is the angular magnification of a telescope that has a 100 cm focal length objective and a 2.50 cm focal length eyepiece?
Solution
−40.0
53. Find the distance between the objective and eyepiece lenses in the telescope in the above problem needed to produce a final image very far from the observer, where vision is most relaxed. Note that a telescope is normally used to view very distant objects.
54. A large reflecting telescope has an objective mirror with a 10.0 m radius of curvature. What angular magnification does it produce when a 3.00 cm focal length eyepiece is used?
Solution
−167
55. A small telescope has a concave mirror with a 2.00 m radius of curvature for its objective. Its eyepiece is a 4.00 cm focal length lens.
(a) What is the telescope’s angular magnification?
(b) What angle is subtended by a 25,000 km diameter sunspot?
(c) What is the angle of its telescopic image?
56. A \(\displaystyle 7.5×\) binocular produces an angular magnification of \(\displaystyle −7.50\), acting like a telescope. (Mirrors are used to make the image upright.) If the binoculars have objective lenses with a 75.0 cm focal length, what is the focal length of the eyepiece lenses?
Solution
+10.0 cm
57. Construct Your Own Problem
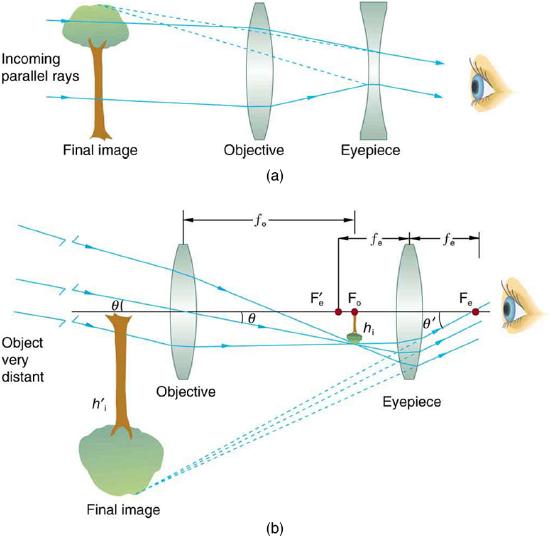
Consider a telescope of the type used by Galileo, having a convex objective and a concave eyepiece as illustrated in Figure(a). Construct a problem in which you calculate the location and size of the image produced. Among the things to be considered are the focal lengths of the lenses and their relative placements as well as the size and location of the object. Verify that the angular magnification is greater than one. That is, the angle subtended at the eye by the image is greater than the angle subtended by the object.
26.6: Aberrations
58. Integrated Concepts
(a) During laser vision correction, a brief burst of 193 nm ultraviolet light is projected onto the cornea of the patient. It makes a spot 1.00 mm in diameter and deposits 0.500 mJ of energy. Calculate the depth of the layer ablated, assuming the corneal tissue has the same properties as water and is initially at \(\displaystyle 34.0ºC\). The tissue’s temperature is increased to \(\displaystyle 100ºC\) and evaporated without further temperature increase.
(b) Does your answer imply that the shape of the cornea can be finely controlled?
Solution
(a) \(\displaystyle 0.251μm\)
(b) Yes, this thickness implies that the shape of the cornea can be very finely controlled, producing normal distant vision in more than 90% of patients.
Contributors and Attributions
Paul Peter Urone (Professor Emeritus at California State University, Sacramento) and Roger Hinrichs (State University of New York, College at Oswego) with Contributing Authors: Kim Dirks (University of Auckland) and Manjula Sharma (University of Sydney). This work is licensed by OpenStax University Physics under a Creative Commons Attribution License (by 4.0).

