Skip to main content
Physics LibreTexts

7.1: Introduction

  1. Last updated
  2. Save as PDF
  • Page ID
    14473
    • Boundless
    • Boundless

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    Linear Momentum

    Linear momentum is the product of the mass and velocity of an object, it is conserved in elastic and inelastic collisions.

    learning objectives

    • Calculate the momentum of two colliding objects

    In classical mechanics, linear momentum, or simply momentum (SI unit kg m/s, or equivalently N s), is the product of the mass and velocity of an object. Mathematically it is stated as:

    \[\mathrm{p=mv}\]

    (Note here that p and v are vectors. ) Like velocity, linear momentum is a vector quantity, possessing a direction as well as a magnitude. Linear momentum is particularly important because it is a conserved quantity, meaning that in a closed system (without any external forces ) its total linear momentum cannot change.

    Because momentum has a direction, it can be used to predict the resulting direction of objects after they collide, as well as their speeds. Momentum is conserved in both inelastic and elastic collisions. (Kinetic energy is not conserved in inelastic collisions but is conserved in elastic collisions. ) It important to note that if the collision takes place on a surface with friction, or if there is air resistance, we would need to account for the momentum of the bodies that would be transferred to the surface and/or air.

    Let’s take a look at a simple, one-dimensional example: The momentum of a system of two particles is the sum of their momenta. If two particles have masses m1 and m2, and velocities v1 and v2, the total momentum is:

    \[\mathrm{p=p_1+p_2=m_1v_1+m_2v_2.}\]

    Keep in mind that momentum and velocity are vectors. Therefore, in 1D, if two particles are moving in the same direction, v1 and v2 have the same sign. If the particles are moving in opposite directions they will have opposite signs.

    If two particles were moving on a plane we would choose our xy-plane to be on the plane of motion. We can then write the x and y component of the total momentum as:

    \[\begin{align} \mathrm{p_x} & \mathrm{=p_{1x}+p_{2x}=m_1v_{1x}+m_2v_{2x}} \\ \mathrm{p_y} & \mathrm{=p_{1y}+p_{2y}=m_1v_{1y}+m_2v_{2y}.} \end{align}\]

    If the 2D momentum vector is decomposed into two components, the equations for each component are reduced to its 1D equivalents.

    Momentum, like energy, is important because it is conserved. “Newton’s cradle” shown in is an example of conservation of momentum. As we will discuss in the next concept (on Momentum, Force, and Newton’s Second Law ), in classical mechanics, conservation of linear momentum is implied by Newton’s laws. Only a few physical quantities are conserved in nature. Studying these quantities yields fundamental insight into how nature works.

    image

    Newton’s Cradle: Total momentum of the system (or Cradle) is conserved. (neglecting frictional loss in the system. )

    Momentum, Force, and Newton’s Second Law

    In the most general form, Newton’s 2nd law can be written as \(\mathrm{F=\frac{dp}{dt}}\).

    learning objectives

    • Relate Newton’s Second Law to momentum and force

    In a closed system (one that does not exchange any matter with the outside and is not acted on by outside forces), the total momentum is constant. This fact, known as the law of conservation of momentum, is implied by Newton’s laws of motion. Suppose, for example, that two particles interact. Because of the third law, the forces between them are equal and opposite. If the particles are numbered 1 and 2, the second law states that

    \[\mathrm{\dfrac{dp_1}{dt}=−\dfrac{dp_2}{dt}}\]

    or

    \[\mathrm{\dfrac{d}{dt}(p_1+p_2)=0}\]

    Therefore, total momentum (p1+p2) is constant. If the velocities of the particles are u1 and u2 before the interaction, and afterwards they are v1 and v2, then

    \[\mathrm{m_1u_1+m_2u_2=m_1v_1+m_2v_2}\]

    This law holds regardless of the nature of the interparticle (or internal) force, no matter how complicated the force is between particles. Similarly, if there are several particles, the momentum exchanged between each pair of particles adds up to zero, so the total change in momentum is zero.

    Newton’s Second Law

    Newton actually stated his second law of motion in terms of momentum: The net external force equals the change in momentum of a system divided by the time over which it changes. Using symbols, this law is

    \[\mathrm{F_{net}=\dfrac{Δp}{Δt},}\]

    where \(\mathrm{F_{net}}\) is the net external force, \(\mathrm{Δp}\) is the change in momentum, and \(\mathrm{Δt}\) is the change in time.

    This statement of Newton’s second law of motion includes the more familiar \(\mathrm{F_{net}=ma}\( as a special case. We can derive this form as follows. First, note that the change in momentum \(\mathrm{Δp}\) is given by \(\mathrm{Δp=Δ(mv)}\). If the mass of the system is constant, then \(\mathrm{Δ(mv)=mΔv}\). So for constant mass, Newton’s second law of motion becomes

    \[\mathrm{F_{net}=\dfrac{Δp}{Δt}=\dfrac{mΔv}{Δt}.}\]

    Because \(\mathrm{\frac{Δv}{Δt}=a}\), we get the familiar equation \(\mathrm{F_{net}=ma}\) when the mass of the system is constant. Newton’s second law of motion stated in terms of momentum is more generally applicable because it can be applied to systems where the mass is changing, such as rockets, as well as to systems of constant mass.

    image

    Momentum in a Closed System: In a game of pool, the system of entire balls can be considered a closed system. Therefore, the total momentum of the balls is conserved.

    Impulse

    Impulse, or change in momentum, equals the average net external force multiplied by the time this force acts.

    learning objectives

    • Explain the relationship between change in momentum and the amount of time a force acts

    Impulse

    Forces produce either acceleration or deceleration on moving bodies, and the greater the force acting on an object, the greater its change in velocity and, hence, the greater its change in momentum. However, changing momentum is also related to how long a time the force acts. If a brief force is applied to a stalled automobile, a change in its momentum is produced. The same force applied over an extended period of time produces a greater change in the automobile’s momentum. The quantity of impulse is force × time interval, or in shorthand notation:

    Momentum & Impulse: A brief overview of momentum and impulse for high school physics students.

    \[\mathrm{Impulse=FΔt,}\]

    where F is the net force on the system, and Δt is the duration of the force.

    From Newton’s 2nd law:

    \[\mathrm{F = \dfrac{\Delta p}{\Delta t} \; (\Delta p: change \; in \; momentum),}\]

    change in momentum equals the average net external force multiplied by the time this force acts.

    \[\mathrm{Δp=FΔt.}\]

    Therefore, impulse as defined in the previous paragraph is simply equivalent to p.

    A force sustained over a long time produces more change in momentum than does the same force applied briefly. A small force applied for a long time can produce the same momentum change as a large force applied briefly because it is the product of the force and the time for which it is applied that is important. Impulse is always equal to change in momentum and is measured in Ns (Newton seconds), as both force and the time interval are important in changing momentum.

    Our definition of impulse includes an assumption that the force is constant over the time interval \(\mathrm{Δt}\). Forces are usually not constant. Forces vary considerably even during the brief time intervals considered. It is, however, possible to find an average effective force \(\mathrm{F_{eff}}\) that produces the same result as the corresponding time-varying force. shows a graph of what an actual force looks like as a function of time for a ball bouncing off the floor. The area under the curve has units of momentum and is equal to the impulse or change in momentum between times \(\mathrm{t_1}\) and \(\mathrm{t_2}\). That area is equal to the area inside the rectangle bounded by \(\mathrm{F_{eff}, t_1,}\) and \(\mathrm{t_2}\). Thus, the impulses and their effects are the same for both the actual and effective forces. Equivalently, we can simple find the area under the curve F(t) between \(\mathrm{t_1}\) and \(\mathrm{t_2}\) to compute the impulse in mathematical form:

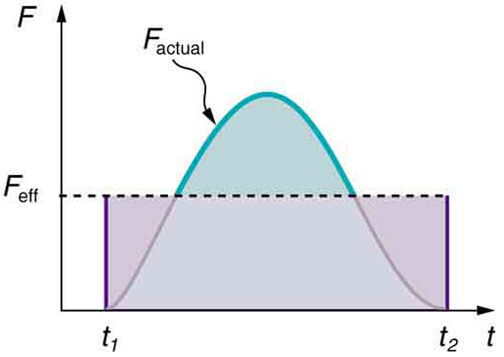
    image

    Force vs. Time: A graph of force versus time with time along the x-axis and force along the y-axis for an actual force and an equivalent effective force. The areas under the two curves are equal.

    \[\mathrm{Impulse=\int_{t_1}^{t_2} F(t)dt.}\]

    Key Points

    • Like velocity, linear momentum is a vector quantity, possessing a direction as well as a magnitude.
    • Momentum, like energy, is important because it is a conserved quantity.
    • The momentum of a system of particles is the sum of their momenta. If two particles have masses m1 and m2, and velocities v1 and v2, the total momentum is \(\mathrm{p=p_1+p_2=m_1v_1+m_2v_2.}\).
    • In a closed system, without any external forces, the total momentum is constant.
    • The familiar equation \(\mathrm{F=ma}\) is a special case of the more general form of the 2nd law when the mass of the system is constant.
    • Momentum conservation holds (in the absence of external force) regardless of the nature of the interparticle (or internal) force, no matter how complicated the force is between particles.
    • A small force applied for a long time can produce the same momentum change as a large force applied briefly, because it is the product of the force and the time for which it is applied that is important.
    • A force produces an acceleration, and the greater the force acting on an object, the greater its change in velocity and, hence, the greater its change in momentum. However, changing momentum is also related to how long a time the force acts.
    • In case of a time-varying force, impulse can be calculated by integrating the force over the time duration. \(\mathrm{Impulse=\int_{t_1}^{t_2} F(t)dt.}\).

    Key Terms

    • inelastic: (As referring to an inelastic collision, in contrast to an elastic collision. ) A collision in which kinetic energy is not conserved.
    • elastic collision: An encounter between two bodies in which the total kinetic energy of the two bodies after the encounter is equal to their total kinetic energy before the encounter. Elastic collisions occur only if there is no net conversion of kinetic energy into other forms.
    • conservation: A particular measurable property of an isolated physical system does not change as the system evolves.
    • closed system: A physical system that doesn’t exchange any matter with its surroundings and isn’t subject to any force whose source is external to the system.
    • momentum: (of a body in motion) the product of its mass and velocity.
    • impulse: The integral of force over time.

    LICENSES AND ATTRIBUTIONS

    CC LICENSED CONTENT, SHARED PREVIOUSLY

    CC LICENSED CONTENT, SPECIFIC ATTRIBUTION

    This page titled 7.1: Introduction is shared under a not declared license and was authored, remixed, and/or curated by Boundless.