6.2: Electric Flux
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of this section, you will be able to:
- Define the concept of flux
- Describe electric flux
- Calculate electric flux for a given situation
The concept of flux describes how much of something goes through a given area. More formally, it is the dot product of a vector field (in this chapter, the electric field) with an area. You may conceptualize the flux of an electric field as a measure of the number of electric field lines passing through an area (Figure 6.2.1). The larger the area, the more field lines go through it and, hence, the greater the flux; similarly, the stronger the electric field is (represented by a greater density of lines), the greater the flux. On the other hand, if the area rotated so that the plane is aligned with the field lines, none will pass through and there will be no flux.
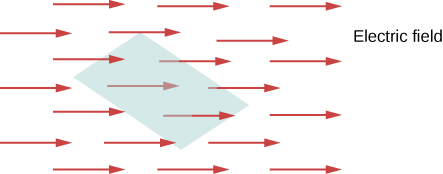
A macroscopic analogy that might help you imagine this is to put a hula hoop in a flowing river. As you change the angle of the hoop relative to the direction of the current, more or less of the flow will go through the hoop. Similarly, the amount of flow through the hoop depends on the strength of the current and the size of the hoop. Again, flux is a general concept; we can also use it to describe the amount of sunlight hitting a solar panel or the amount of energy a telescope receives from a distant star, for example.
To quantify this idea, Figure 6.2.1a shows a planar surface S1 of area A1 that is perpendicular to the uniform electric field →E=Eˆy. If N field lines pass through S1, then we know from the definition of electric field lines (Electric Charges and Fields) that N/A∝E, or N∝EA1.
The quantity EA1 is the electric flux through S1. We represent the electric flux through an open surface like S1 by the symbol Φ. Electric flux is a scalar quantity and has an SI unit of newton-meters squared per coulomb (N⋅m2/C). Notice that N∝EA1 may also be written as N∝Φ, demonstrating that electric flux is a measure of the number of field lines crossing a surface.
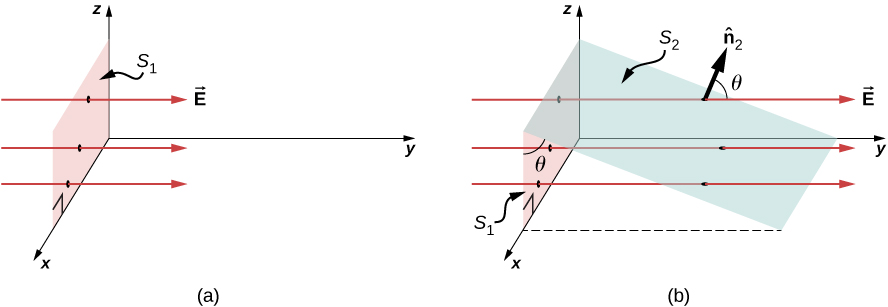
Now consider a planar surface that is not perpendicular to the field. How would we represent the electric flux? Figure 6.2.2b shows a surface S2 of area A2 that is inclined at an angle θ to the xz-plane and whose projection in that plane is S1 (area A1). The areas are related by A2cosθ=A1. Because the same number of field lines crosses both S1 and S2, the fluxes through both surfaces must be the same. The flux through S2 is therefore Φ=EA1=EA2cosθ. Designating ˆn2 as a unit vector normal to S2 (see Figure 6.2.2b), we obtain
Φ=→E⋅ˆn2A2.
Check out this video to observe what happens to the flux as the area changes in size and angle, or the electric field changes in strength.
Area Vector
For discussing the flux of a vector field, it is helpful to introduce an area vector →A. This allows us to write the last equation in a more compact form. What should the magnitude of the area vector be? What should the direction of the area vector be? What are the implications of how you answer the previous question?
The area vector of a flat surface of area →A has the following magnitude and direction:
- Magnitude is equal to area (A)
- Direction is along the normal to the surface (ˆn); that is, perpendicular to the surface.
Since the normal to a flat surface can point in either direction from the surface, the direction of the area vector of an open surface needs to be chosen, as shown in Figure 6.2.3.
Since ˆn is a unit normal to a surface, it has two possible directions at every point on that surface (Figure 6.2.1a). For an open surface, we can use either direction, as long as we are consistent over the entire surface. 6.2.1c of the figure shows several cases.
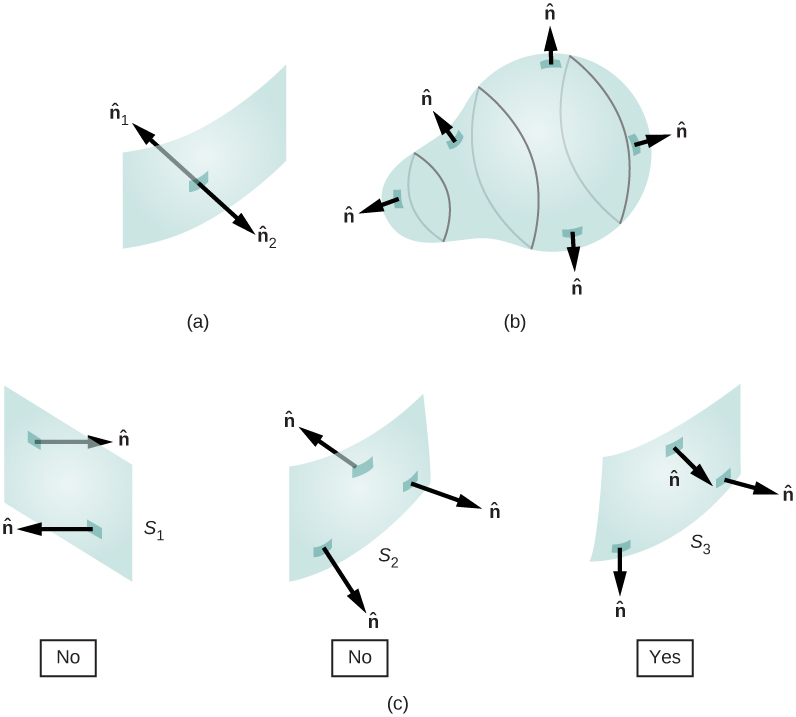
However, if a surface is closed, then the surface encloses a volume. In that case, the direction of the normal vector at any point on the surface points from the inside to the outside. On a closed surface such as that of Figure 6.2.1b, ˆn is chosen to be the outward normal at every point, to be consistent with the sign convention for electric charge.
Electric Flux
Now that we have defined the area vector of a surface, we can define the electric flux of a uniform electric field through a flat area as the scalar product of the electric field and the area vector:
Φ=→E⋅→A (uniform →E,flat surface).
Figure 6.2.5 shows the electric field of an oppositely charged, parallel-plate system and an imaginary box between the plates. The electric field between the plates is uniform and points from the positive plate toward the negative plate. A calculation of the flux of this field through various faces of the box shows that the net flux through the box is zero. Why does the flux cancel out here?

The reason is that the sources of the electric field are outside the box. Therefore, if any electric field line enters the volume of the box, it must also exit somewhere on the surface because there is no charge inside for the lines to land on. Therefore, quite generally, electric flux through a closed surface is zero if there are no sources of electric field, whether positive or negative charges, inside the enclosed volume. In general, when field lines leave (or “flow out of”) a closed surface, Φ is positive; when they enter (or “flow into”) the surface, Φ is negative.
Any smooth, non-flat surface can be replaced by a collection of tiny, approximately flat surfaces, as shown in Figure 6.2.6. If we divide a surface S into small patches, then we notice that, as the patches become smaller, they can be approximated by flat surfaces. This is similar to the way we treat the surface of Earth as locally flat, even though we know that globally, it is approximately spherical.
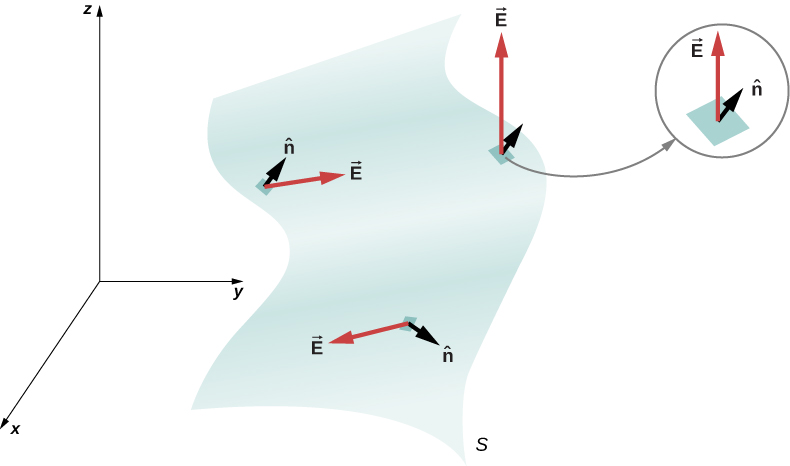
To keep track of the patches, we can number them from 1 through N. Now, we define the area vector for each patch as the area of the patch pointed in the direction of the normal. Let us denote the area vector for the ith patch by δ→Ai. (We have used the symbol δ to remind us that the area is of an arbitrarily small patch.) With sufficiently small patches, we may approximate the electric field over any given patch as uniform. Let us denote the average electric field at the location of the ith patch by →Ei.
→Ei=average electric field over the ith patch.
Therefore, we can write the electric flux Φ through the area of the ith patch as
Φi=→Ei⋅δ→Ai (ithpatch).
The flux through each of the individual patches can be constructed in this manner and then added to give us an estimate of the net flux through the entire surface S, which we denote simply as Φ.
Φ=N∑i=1Φi=N∑i=1→Ei⋅δ→Ai (N patch estimate).
This estimate of the flux gets better as we decrease the size of the patches. However, when you use smaller patches, you need more of them to cover the same surface. In the limit of infinitesimally small patches, they may be considered to have area dA and unit normal ˆn. Since the elements are infinitesimal, they may be assumed to be planar, and →Ei may be taken as constant over any element. Then the flux dΦ through an area dA is given by dΦ=→E⋅ˆndA. It is positive when the angle between →Ei and ˆn is less than 90∘ and negative when the angle is greater than 90o. The net flux is the sum of the infinitesimal flux elements over the entire surface. With infinitesimally small patches, you need infinitely many patches, and the limit of the sum becomes a surface integral. With ∫S representing the integral over S,
Φ=∫S→E⋅ˆndA=∫S→E⋅d→A (open surface).
In practical terms, surface integrals are computed by taking the antiderivatives of both dimensions defining the area, with the edges of the surface in question being the bounds of the integral.
To distinguish between the flux through an open surface like that of Figure 6.2.2 and the flux through a closed surface (one that completely bounds some volume), we represent flux through a closed surface by
Φ=∮S→E⋅ˆndA=∮S→E⋅d→A (closed surface)
where the circle through the integral symbol simply means that the surface is closed, and we are integrating over the entire thing. If you only integrate over a portion of a closed surface, that means you are treating a subset of it as an open surface.
A constant electric field of magnitude E0 points in the direction of the positive z-axis (Figure 6.2.7). What is the electric flux through a rectangle with sides a and b in the (a) xy-plane and in the (b) xz-plane?

Strategy
Apply the definition of flux: Φ=→E⋅→A (uniform →E), where the definition of dot product is crucial.
Solution
- In this case, Φ=→E0⋅→A=E0A=E0ab.
- Here, the direction of the area vector is either along the positive y-axis or toward the negative y-axis. Therefore, the scalar product of the electric field with the area vector is zero, giving zero flux.
Significance
The relative directions of the electric field and area can cause the flux through the area to be zero.
A constant electric field of magnitude E0 points in the direction of the positive z-axis (Figure 6.2.8). What is the net electric flux through a cube?

Strategy
Apply the definition of flux: Φ=→E⋅→A (uniform →E), noting that a closed surface eliminates the ambiguity in the direction of the area vector.
Solution
Through the top face of the cube Φ=→E0⋅→A=E0A.
Through the bottom face of the cube, Φ=→E0⋅→A=−E0A, because the area vector here points downward.
Along the other four sides, the direction of the area vector is perpendicular to the direction of the electric field. Therefore, the scalar product of the electric field with the area vector is zero, giving zero flux.
The net flux is Φnet=E0A−E0A+0+0+0+0=0.
Significance
The net flux of a uniform electric field through a closed surface is zero.
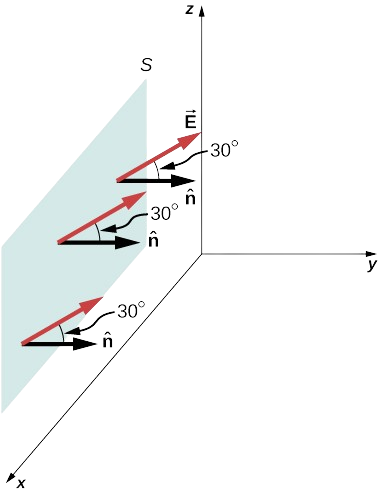
A uniform electric field →E of magnitude 10 N/C is directed parallel to the yz-plane at 30∘ above the xy-plane, as shown in Figure 6.2.9. What is the electric flux through the plane surface of area 6.0m2 located in the xz-plane? Assume that ˆn points in the positive y-direction.
Strategy
Apply Φ=∫S→E⋅ˆndA, where the direction and magnitude of the electric field are constant.
Solution
The angle between the uniform electric field →E and the unit normal ˆn to the planar surface is 30∘. Since both the direction and magnitude are constant, E comes outside the integral. All that is left is a surface integral over dA, which is A. Therefore, using the open-surface equation, we find that the electric flux through the surface is
Φ=∫S→E⋅ˆndA=EAcosθ
=(10N/C)(6.0m2)(cos30∘)=52N⋅m2/C.
Significance
Again, the relative directions of the field and the area matter, and the general equation with the integral will simplify to the simple dot product of area and electric field.
What angle should there be between the electric field and the surface shown in Figure 6.2.9 in the previous example so that no electric flux passes through the surface?
- Answer
-
Place it so that its unit normal is perpendicular to →E.
What is the total flux of the electric field →E=cy2ˆk through the rectangular surface shown in Figure 6.2.10?
.png?revision=2)
Strategy
Apply Φ=∫S→E⋅ˆndA. We assume that the unit normal ˆn to the given surface points in the positive z-direction, so ˆn=ˆk. Since the electric field is not uniform over the surface, it is necessary to divide the surface into infinitesimal strips along which →E is essentially constant. As shown in Figure 6.2.10, these strips are parallel to the x-axis, and each strip has an area dA=bdy.
Solution
From the open surface integral, we find that the net flux through the rectangular surface is
Φ=∫S→E⋅ˆndA=∫a0(cy2ˆk)⋅ˆk(bdy)=cb∫a0y2dy=13a3bc.
Significance
For a non-constant electric field, the integral method is required.
If the electric field in Example 6.2.4 is →E=mxˆk. what is the flux through the rectangular area?
- Answer
-
mab2/2


