10.3: Resistors in Series and Parallel
- Page ID
- 4408
By the end of the section, you will be able to:
- Define the term equivalent resistance
- Calculate the equivalent resistance of resistors connected in series
- Calculate the equivalent resistance of resistors connected in parallel
In Current and Resistance, we described the term ‘resistance’ and explained the basic design of a resistor. Basically, a resistor limits the flow of charge in a circuit and is an ohmic device where \(V = IR\). Most circuits have more than one resistor. If several resistors are connected together and connected to a battery, the current supplied by the battery depends on the equivalent resistance of the circuit.
The equivalent resistance of a combination of resistors depends on both their individual values and how they are connected. The simplest combinations of resistors are series and parallel connections (Figure \(\PageIndex{1}\)). In a series circuit, the output current of the first resistor flows into the input of the second resistor; therefore, the current is the same in each resistor. In a parallel circuit, all of the resistor leads on one side of the resistors are connected together and all the leads on the other side are connected together. In the case of a parallel configuration, each resistor has the same potential drop across it, and the currents through each resistor may be different, depending on the resistor. The sum of the individual currents equals the current that flows into the parallel connections.
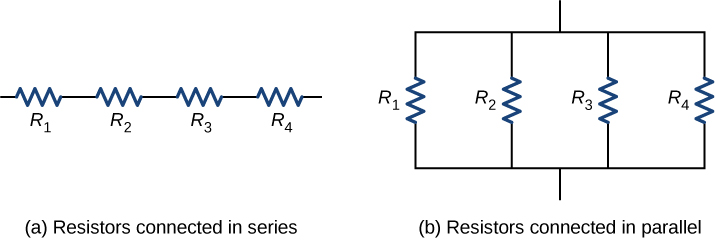
Resistors in Series
Resistors are said to be in series whenever the current flows through the resistors sequentially. Consider Figure \(\PageIndex{2}\), which shows three resistors in series with an applied voltage equal to \(V_{ab}\). Since there is only one path for the charges to flow through, the current is the same through each resistor. The equivalent resistance of a set of resistors in a series connection is equal to the algebraic sum of the individual resistances.
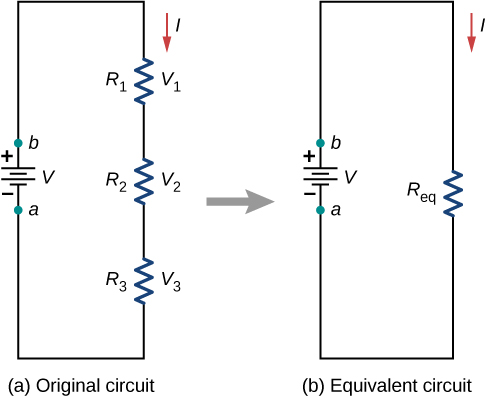
In Figure \(\PageIndex{2}\), the current coming from the voltage source flows through each resistor, so the current through each resistor is the same. The current through the circuit depends on the voltage supplied by the voltage source and the resistance of the resistors. For each resistor, a potential drop occurs that is equal to the loss of electric potential energy as a current travels through each resistor. According to Ohm’s law, the potential drop \(V\) across a resistor when a current flows through it is calculated using the equation \(V = IR\), where \(I\) is the current in amps (\(A\)) and \(R\) is the resistance in ohms \((\Omega)\). Since energy is conserved, and the voltage is equal to the potential energy per charge, the sum of the voltage applied to the circuit by the source and the potential drops across the individual resistors around a loop should be equal to zero:
\[\sum_{i = 1}^N V_i = 0.\]
This equation is often referred to as Kirchhoff’s loop law, which we will look at in more detail later in this chapter. For Figure \(\PageIndex{2}\), the sum of the potential drop of each resistor and the voltage supplied by the voltage source should equal zero:
\[\begin{align*} V - V_1 - V_2 - V_3 &= 0, \\[4pt] V &= V_1 + V_2 + V_3, \\[4pt] &= IR_1 + IR_2 + IR_3, \end{align*}\]
Solving for \(I\)
\[\begin{align*} I &= \frac{V}{R_1 + R_2 + R_3} \\[4pt] &= \frac{V}{R_{S}}. \end{align*}\]
Since the current through each component is the same, the equality can be simplified to an equivalent resistance (\(R_{S}\)), which is just the sum of the resistances of the individual resistors.
Any number of resistors can be connected in series. If \(N\) resistors are connected in series, the equivalent resistance is
\[R_{S} = R_1 + R_2 + R_3 + . . . + R_{N-1} + R_N = \sum_{i=1}^N R_i. \label{equivalent resistance series}\]
One result of components connected in a series circuit is that if something happens to one component, it affects all the other components. For example, if several lamps are connected in series and one bulb burns out, all the other lamps go dark.
A battery with a terminal voltage of 9 V is connected to a circuit consisting of four \(20 \, \Omega\) and one \(10 \, \Omega\) resistors all in series (Figure \(\PageIndex{3}\)). Assume the battery has negligible internal resistance.
- Calculate the equivalent resistance of the circuit.
- Calculate the current through each resistor.
- Calculate the potential drop across each resistor.
- Determine the total power dissipated by the resistors and the power supplied by the battery.
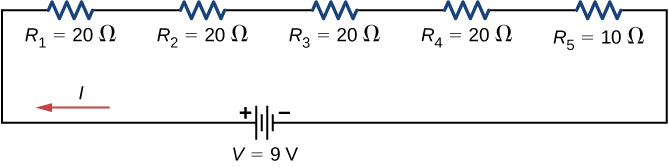
Strategy
In a series circuit, the equivalent resistance is the algebraic sum of the resistances. The current through the circuit can be found from Ohm’s law and is equal to the voltage divided by the equivalent resistance. The potential drop across each resistor can be found using Ohm’s law. The power dissipated by each resistor can be found using \(P = I^2R\), and the total power dissipated by the resistors is equal to the sum of the power dissipated by each resistor. The power supplied by the battery can be found using \(P = I\epsilon\).
Solution
- The equivalent resistance is the algebraic sum of the resistances (Equation \ref{equivalent resistance series}): \[\begin{align*} R_{S} &= R_1 + R_2 + R_3 + R_4 + R_5 \\[4pt] &= 20 \, \Omega + 20 \, \Omega + 20 \, \Omega + 20 \, \Omega + 10 \, \Omega = 90 \, \Omega. \end{align*}\]
- The current through the circuit is the same for each resistor in a series circuit and is equal to the applied voltage divided by the equivalent resistance: \[I = \frac{V}{R_{S}} = \frac{9 \, V}{90 \, \Omega} = 0.1 \, A. \nonumber\] Note that the sum of the potential drops across each resistor is equal to the voltage supplied by the battery.
- The power dissipated by a resistor is equal to \(P = I^2R\), and the power supplied by the battery is equal to \(P = I\epsilon\). \[P_1 = P_2 = P_3 = P_4 = (0.1 \, A)^2 (20 \, \Omega) = 0.2 \, W,\nonumber\] \[P_5 = (0.1 \, A)^2 (10 \, \Omega) = 0.1 \, W,\nonumber\] \[P_{dissipated} = 0.2 \, W + 0.2 \, W + 0.2 \, W + 0.2 \, W + 0.1 \, W = 0.9 \, W,\nonumber\] \[P_{source} = I\epsilon = (0.1 \, A)(9 \, V) = 0.9 \, W. \nonumber\]
Significance
There are several reasons why we would use multiple resistors instead of just one resistor with a resistance equal to the equivalent resistance of the circuit. Perhaps a resistor of the required size is not available, or we need to dissipate the heat generated, or we want to minimize the cost of resistors. Each resistor may cost a few cents to a few dollars, but when multiplied by thousands of units, the cost saving may be appreciable.
Some strings of miniature holiday lights are made to short out when a bulb burns out. The device that causes the short is called a shunt, which allows current to flow around the open circuit. A “short” is like putting a piece of wire across the component. The bulbs are usually grouped in series of nine bulbs. If too many bulbs burn out, the shunts eventually open. What causes this?
- Answer
-
The equivalent resistance of nine bulbs connected in series is 9R. The current is \(I = V/9 \, R\). If one bulb burns out, the equivalent resistance is 8R, and the voltage does not change, but the current increases \((I = V/8 \, R\). As more bulbs burn out, the current becomes even higher. Eventually, the current becomes too high, burning out the shunt.
Let’s briefly summarize the major features of resistors in series:
- Series resistances add together to get the equivalent resistance (Equation \ref{equivalent resistance series}): \[R_{S} = R_1 + R_2 + R_3 + . . . + R_{N-1} + R_N = \sum_{i=1}^N R_i.\]
- The same current flows through each resistor in series.
- Individual resistors in series do not get the total source voltage, but divide it. The total potential drop across a series configuration of resistors is equal to the sum of the potential drops across each resistor.
Resistors in Parallel
Figure \(\PageIndex{4}\) shows resistors in parallel, wired to a voltage source. Resistors are in parallel when one end of all the resistors are connected by a continuous wire of negligible resistance and the other end of all the resistors are also connected to one another through a continuous wire of negligible resistance. The potential drop across each resistor is the same. Current through each resistor can be found using Ohm’s law \(I = V/R\), where the voltage is constant across each resistor. For example, an automobile’s headlights, radio, and other systems are wired in parallel, so that each subsystem utilizes the full voltage of the source and can operate completely independently. The same is true of the wiring in your house or any building.
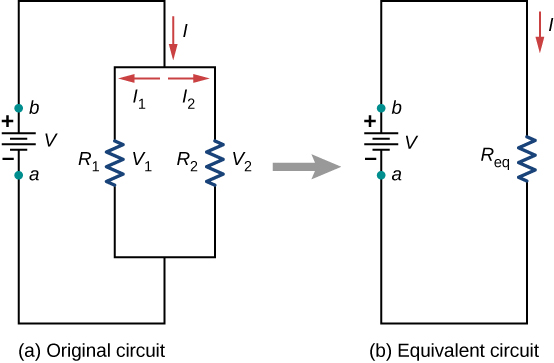
The current flowing from the voltage source in Figure \(\PageIndex{4}\) depends on the voltage supplied by the voltage source and the equivalent resistance of the circuit. In this case, the current flows from the voltage source and enters a junction, or node, where the circuit splits flowing through resistors \(R_1\) and \(R_2\). As the charges flow from the battery, some go through resistor \(R_1\) and some flow through resistor \(R_2\). The sum of the currents flowing into a junction must be equal to the sum of the currents flowing out of the junction:
\[\sum I_{in} = \sum I_{out}. \nonumber\]
This equation is referred to as Kirchhoff’s junction rule and will be discussed in detail in the next section. In Figure \(\PageIndex{4}\), the junction rule gives \(I = I_1 + I_2\). There are two loops in this circuit, which leads to the equations \(V = I_1R_1\) and \(I_1R_1 = I_2R_2\). Note the voltage across the resistors in parallel are the same ( \(V = V_1 = V_2\)) and the current is additive:
\[ \begin{align*} I &= I_1 + I_2 \\[4pt] &= \frac{V_1}{R_1} + \frac{V_2}{R_2} \\[4pt] &= \frac{V}{R_1} + \frac{V}{R_2} \\[4pt] &= V \left( \frac{1}{R_1} + \frac{1}{R_2} \right) = \frac{V}{R_{P}}\end{align*}\]
Solving for the \(R_{P}\)
\[R_{P} = \left(\frac{1}{R_1} + \frac{1}{R_2} \right)^{-1}. \]
Generalizing to any number of \(N\) resistors, the equivalent resistance \(R_{P}\) of a parallel connection is related to the individual resistances by
\[R_{P} = \left( \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + . . . + \frac{1}{R_{N-1}} + \frac{1}{R_N} \right)^{-1} = \left(\sum_{i=1}^N \frac{1}{R_i} \right)^{-1}. \label{10.3}\]
This relationship results in an equivalent resistance \(R_{P}\) that is less than the smallest of the individual resistances. When resistors are connected in parallel, more current flows from the source than would flow for any of them individually, so the total resistance is lower.
Three resistors \(R_1 = 1.00 \, \Omega\), \(R_2 = 2.00 \, \Omega\), and \(R_3 = 2.00 \, \Omega\), are connected in parallel. The parallel connection is attached to a \(V = 3.00 \, V\) voltage source.
- What is the equivalent resistance?
- Find the current supplied by the source to the parallel circuit.
- Calculate the currents in each resistor and show that these add together to equal the current output of the source.
- Calculate the power dissipated by each resistor.
- Find the power output of the source and show that it equals the total power dissipated by the resistors.
Strategy
(a) The total resistance for a parallel combination of resistors is found using Equation \ref{10.3}. (Note that in these calculations, each intermediate answer is shown with an extra digit.)
(b) The current supplied by the source can be found from Ohm’s law, substituting \(R_{P}\) for the total resistance \(I = \frac{V}{R_{P}}\).
(c) The individual currents are easily calculated from Ohm’s law \(\left(I_i = \frac{V_i}{R_i}\right)\), since each resistor gets the full voltage. The total current is the sum of the individual currents: \[I = \sum_i I_i. \nonumber\]
(d) The power dissipated by each resistor can be found using any of the equations relating power to current, voltage, and resistance, since all three are known. Let us use \(P_i = V^2 /R_i\), since each resistor gets full voltage.
(e) The total power can also be calculated in several ways, use \(P = IV\).
Solution
- The total resistance for a parallel combination of resistors is found using Equation \ref{10.3}. Entering known values gives \[R_{P} = \left( \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} \right)^{-1} = \left(\frac{1}{1.00 \, \Omega} + \frac{1}{2.00 \, \Omega} + \frac{1}{2.00 \, \Omega} \right)^{-1} = 0.50 \, \Omega.\nonumber\] The total resistance with the correct number of significant digits is \(R_{eq} = 0.50 \, \Omega\). As predicted, \(R_{P}\) is less than the smallest individual resistance.
- The total current can be found from Ohm’s law, substituting \(R_{P}\) for the total resistance. This gives \[I = \frac{V}{R_{P}} = \frac{3.00 \, V}{0.50 \, \Omega} = 6.00 \, A.\nonumber\] Current I for each device is much larger than for the same devices connected in series (see the previous example). A circuit with parallel connections has a smaller total resistance than the resistors connected in series.
- The individual currents are easily calculated from Ohm’s law, since each resistor gets the full voltage. Thus, \[I_1 = \frac{V}{R_1} = \frac{3.00 \, V}{1.00 \, \Omega} = 3.00 \, A.\nonumber\] Similarly, \[I_2 = \frac{V}{R_2} = \frac{3.00 \, V}{2.00 \, \Omega} = 1.50 \, A\nonumber\] and \[I_3 = \frac{V}{R_3} = \frac{3.00 \, V}{2.00 \, \Omega} = 1.50 \, A.\nonumber\] The total current is the sum of the individual currents: \[I_1 + I_2 + I_3 = 6.00 \, A.\nonumber\]
- The power dissipated by each resistor can be found using any of the equations relating power to current, voltage, and resistance, since all three are known. Let us use \(P = V^2 /R\), since each resistor gets full voltage. Thus, \[P_1 = \frac{V^2}{R_1} = \frac{(3.00 \, V)^2}{1.00 \, \Omega} = 9.00 \, W.\nonumber\] Similarly, \[P_2 = \frac{V^2}{R_2} = \frac{(3.00 \, V)^2}{2.00 \, \Omega} = 4.50 \, W.\nonumber\] and \[P_3 = \frac{V^2}{R_3} = \frac{(3.00 \, V)^2}{2.00 \, \Omega} = 4.50 \, W.\nonumber\]
- The total power can also be calculated in several ways. Choosing \(P = IV\) and entering the total current yields \[P = IV = (6.00 \, A)(3.00 \, V) = 18.00 \, W.\nonumber\]
Significance
Total power dissipated by the resistors is also 18.00 W:
\[P_1 + P_2 + P_3 = 9.00 \, W + 4.50 \, W + 4.50 \, W = 18.00 \, W.\nonumber\]
Notice that the total power dissipated by the resistors equals the power supplied by the source.
Consider the same potential difference \((V = 3.00 \, V)\) applied to the same three resistors connected in series. Would the equivalent resistance of the series circuit be higher, lower, or equal to the three resistor in parallel? Would the current through the series circuit be higher, lower, or equal to the current provided by the same voltage applied to the parallel circuit? How would the power dissipated by the resistor in series compare to the power dissipated by the resistors in parallel?
- Solution
-
The equivalent of the series circuit would be \(R_{eq} = 1.00 \, \Omega + 2.00 \, \Omega + 2.00 \, \Omega = 5.00 \, \Omega\), which is higher than the equivalent resistance of the parallel circuit \(R_{eq} = 0.50 \, \Omega\). The equivalent resistor of any number of resistors is always higher than the equivalent resistance of the same resistors connected in parallel. The current through for the series circuit would be \(I = \frac{3.00 \, V}{5.00 \, \Omega} = 0.60 \, A\), which is lower than the sum of the currents through each resistor in the parallel circuit, \(I = 6.00 \, A\). This is not surprising since the equivalent resistance of the series circuit is higher. The current through a series connection of any number of resistors will always be lower than the current into a parallel connection of the same resistors, since the equivalent resistance of the series circuit will be higher than the parallel circuit. The power dissipated by the resistors in series would be \(P = 1.800 \, W\), which is lower than the power dissipated in the parallel circuit \(P = 18.00 \, W\).
How would you use a river and two waterfalls to model a parallel configuration of two resistors? How does this analogy break down?
- Solution
-
A river, flowing horizontally at a constant rate, splits in two and flows over two waterfalls. The water molecules are analogous to the electrons in the parallel circuits. The number of water molecules that flow in the river and falls must be equal to the number of molecules that flow over each waterfall, just like sum of the current through each resistor must be equal to the current flowing into the parallel circuit. The water molecules in the river have energy due to their motion and height. The potential energy of the water molecules in the river is constant due to their equal heights. This is analogous to the constant change in voltage across a parallel circuit. Voltage is the potential energy across each resistor.
The analogy quickly breaks down when considering the energy. In the waterfall, the potential energy is converted into kinetic energy of the water molecules. In the case of electrons flowing through a resistor, the potential drop is converted into heat and light, not into the kinetic energy of the electrons.
Let us summarize the major features of resistors in parallel:
- Equivalent resistance is found from Equation \ref{10.3} and is smaller than any individual resistance in the combination.
- The potential drop across each resistor in parallel is the same.
- Parallel resistors do not each get the total current; they divide it. The current entering a parallel combination of resistors is equal to the sum of the current through each resistor in parallel.
In this chapter, we introduced the equivalent resistance of resistors connect in series and resistors connected in parallel. You may recall from the Section on Capacitance, we introduced the equivalent capacitance of capacitors connected in series and parallel. Circuits often contain both capacitors and resistors. Table \(\PageIndex{1}\) summarizes the equations used for the equivalent resistance and equivalent capacitance for series and parallel connections.
| Series combination | Parallel combination | |
|---|---|---|
| Equivalent capacitance | \[\frac{1}{C_{S} }= \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} + . . . \nonumber\] | \[C_{P} = C_1 + C_2 + C_3 + . . . \nonumber\] |
| Equivalent resistance | \[R_{S} = R_1 + R_2 + R_3 + . . . = \sum_{i=1}^N R_i \nonumber\] | \[\frac{1}{R_{P}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + . . . \nonumber\] |
Combinations of Series and Parallel
More complex connections of resistors are often just combinations of series and parallel connections. Such combinations are common, especially when wire resistance is considered. In that case, wire resistance is in series with other resistances that are in parallel.
Combinations of series and parallel can be reduced to a single equivalent resistance using the technique illustrated in Figure \(\PageIndex{5}\). Various parts can be identified as either series or parallel connections, reduced to their equivalent resistances, and then further reduced until a single equivalent resistance is left. The process is more time consuming than difficult. Here, we note the equivalent resistance as \(R_{eq}\).
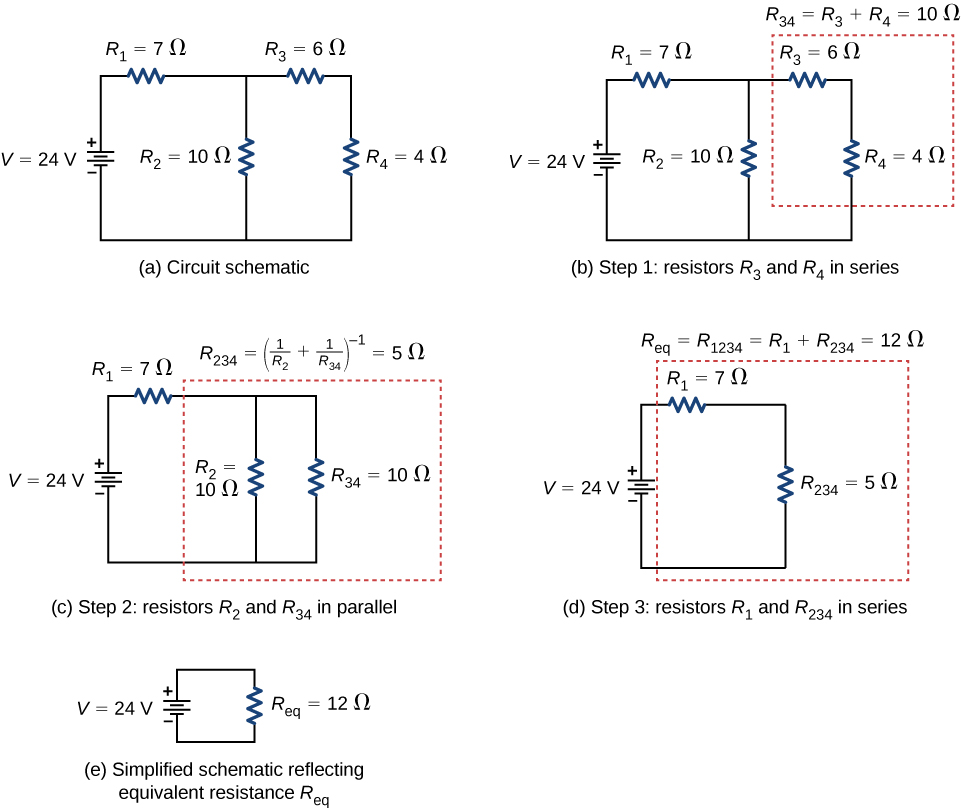
Notice that resistors \(R_3\) and \(R_4\) are in series. They can be combined into a single equivalent resistance. One method of keeping track of the process is to include the resistors as subscripts. Here the equivalent resistance of \(R_3\) and \(R_4\) is
\[R_{34} = R_3 + R_4 = 6 \, \Omega + 4 \, \Omega = 10 \, \Omega. \nonumber\]
The circuit now reduces to three resistors, shown in Figure \(\PageIndex{5c}\). Redrawing, we now see that resistors \(R_2\) and \(R_{34}\) constitute a parallel circuit. Those two resistors can be reduced to an equivalent resistance:
\[R_{234} = \left( \frac{1}{R_2} + \frac{1}{R_{34}}\right)^{-1} = \left(\frac{1}{10 \, \Omega} + \frac{1}{10 \, \Omega} \right)^{-1} = 5 \, \Omega. \nonumber\]
This step of the process reduces the circuit to two resistors, shown in in Figure \(\PageIndex{5d}\). Here, the circuit reduces to two resistors, which in this case are in series. These two resistors can be reduced to an equivalent resistance, which is the equivalent resistance of the circuit:
\[R_{eq} = R_{1234} = R_1 + R_{234} = 7 \, \Omega + 5 \Omega = 12 \, \Omega. \nonumber\]
The main goal of this circuit analysis is reached, and the circuit is now reduced to a single resistor and single voltage source.
Now we can analyze the circuit. The current provided by the voltage source is \(I = \frac{V}{R_{eq}} = \frac{24 \, V}{12 \, \Omega} = 2 \, A\). This current runs through resistor \(R_1\) and is designated as \(I_1\). The potential drop across \(R_1\) can be found using Ohm’s law:
\[V_1 = I_1R_1 = (2 \, A)(7 \, \Omega) = 14 \, V. \nonumber\]
Looking at Figure \(\PageIndex{5c}\), this leaves \(24 \, V - 14 \, V = 10 \, V\) to be dropped across the parallel combination of \(R_2\) and \(R_{34}\). The current through \(R_2\) can be found using Ohm’s law:
\[I_2 = \frac{V_2}{R_2} = \frac{10 \, V}{10 \, \Omega} = 1 \, A. \nonumber\]
The resistors \(R_3\) and \(R_4\) are in series so the currents \(I_3\) and \(I_4\) are equal to
\[I_3 = I_4 = I - I_2 = 2 \, A - 1 \, A = 1 \, A. \nonumber\]
Using Ohm’s law, we can find the potential drop across the last two resistors. The potential drops are \(V_3 = I_3R_3 = 6 \, V\) and \(V_4 = I_4R_4 = 4 \, V\). The final analysis is to look at the power supplied by the voltage source and the power dissipated by the resistors. The power dissipated by the resistors is
\[\begin{align*}P_1 &= I_1^2R_1 = (2 \, A)^2 (7 \, \Omega) = 28 \, W, \\[4pt] P_2 &= I_2^2R_2 = (1 \, A)^2 (10 \, \Omega) = 10 \, W, \\[4pt] P_3 &= I_3^2R_3 = (1 \, A)^2 (6 \, \Omega) = 6 \, W, \\[4pt] P_4 &= I_4^2R_4 = (1 \, A)^2 (4 \, \Omega) = 4 \, W, \\[4pt] P_{dissipated} &= P_1 + P_2 + P_3 + P_4 = 48 \, W. \end{align*}\]
The total energy is constant in any process. Therefore, the power supplied by the voltage source is
\[\begin{align*} P_s &= IV \\[4pt] &= (2 \, A)(24 \, V) = 48 \, W \end{align*}\]
Analyzing the power supplied to the circuit and the power dissipated by the resistors is a good check for the validity of the analysis; they should be equal.
Figure \(\PageIndex{6}\) shows resistors wired in a combination of series and parallel. We can consider \(R_1\) to be the resistance of wires leading to \(R_2\) and \(R_3\).
- Find the equivalent resistance of the circuit.
- What is the potential drop \(V_1\) across resistor \(R_1\)?
- Find the current \(I_2\) through resistor \(R_2\).
- What power is dissipated by \(R_2\)?
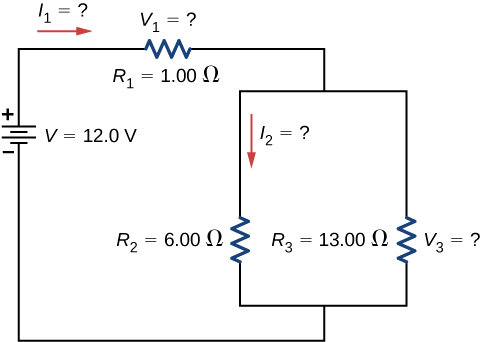
Strategy
(a) To find the equivalent resistance, first find the equivalent resistance of the parallel connection of \(R_2\) and \(R_3\). Then use this result to find the equivalent resistance of the series connection with \(R_1\).
(b) The current through \(R_1\) can be found using Ohm’s law and the voltage applied. The current through \(R_1\) is equal to the current from the battery. The potential drop \(V_1\) across the resistor \(R_1\) (which represents the resistance in the connecting wires) can be found using Ohm’s law.
(c) The current through \(R_2\) can be found using Ohm’s law \(I_2 = \frac{V_2}{R_2}\). The voltage across \(R_2\) can be found using \(V_2 = V - V_1\).
(d) Using Ohm’s law \((V_2 = I_2R_2)\), the power dissipated by the resistor can also be found using \(P_2 = I_2^2 R_2 = \frac{V_2^2}{R_2}\).
Solution
- To find the equivalent resistance of the circuit, notice that the parallel connection of \(R_2\) and \(R_3\) is in series with \(R_1\), so the equivalent resistance is \[R_{eq} = R_1 + \left(\frac{1}{R_2} + \frac{1}{R_3} \right)^{-1} = 1.00 \, \Omega + \left(\frac{1}{6.00 \, \Omega} + \frac{1}{13.00 \, \Omega}\right)^{-1} = 5.10 \, \Omega.\nonumber\] The total resistance of this combination is intermediate between the pure series and pure parallel values (\(20.0 \, \Omega\) and \(0.804 \, \Omega\), respectively).
- The current through \(R_1\) is equal to the current supplied by the battery: \[I_1 = I = \frac{V}{R_{eq}} = \frac{12.0 \, V}{5.10 \, \Omega} = 2.35 \, A.\nonumber\] The voltage across \(R_1\) is \[V_1 = I_1R_1 = (2.35 \, A)(1 \, \Omega) = 2.35 \, V.\nonumber\] The voltage applied to \(R_2\) and \(R_3\) is less than the voltage supplied by the battery by an amount \(V_1\). When wire resistance is large, it can significantly affect the operation of the devices represented by \(R_2\) and \(R_3\).
- To find the current through \(R_2\), we must first find the voltage applied to it. The voltage across the two resistors in parallel is the same: \[V_2 = V_3 = V - V_1 = 12.0 \, V - 2.35 \, V = 9.65 \, V.\nonumber\] Now we can find the current \(I_2\) through resistance \(R_2\) using Ohm’s law: \[I_2 = \frac{V_2}{R_2} = \frac{9.65 \, V}{6.00 \, \Omega} = 1.61 \, A.\nonumber\] The current is less than the 2.00 A that flowed through \(R_2\) when it was connected in parallel to the battery in the previous parallel circuit example.
- The power dissipated by \(R_2\) is given by \[P_2 = I_2^2R_2 = (1.61 \, A)^2 (6.00 \, \Omega) = 15.5 \, W. \nonumber\]
Significance
The analysis of complex circuits can often be simplified by reducing the circuit to a voltage source and an equivalent resistance. Even if the entire circuit cannot be reduced to a single voltage source and a single equivalent resistance, portions of the circuit may be reduced, greatly simplifying the analysis.
Consider the electrical circuits in your home. Give at least two examples of circuits that must use a combination of series and parallel circuits to operate efficiently.
- Solution
-
All the overhead lighting circuits are in parallel and connected to the main supply line, so when one bulb burns out, all the overhead lighting does not go dark. Each overhead light will have at least one switch in series with the light, so you can turn it on and off.
A refrigerator has a compressor and a light that goes on when the door opens. There is usually only one cord for the refrigerator to plug into the wall. The circuit containing the compressor and the circuit containing the lighting circuit are in parallel, but there is a switch in series with the light. A thermostat controls a switch that is in series with the compressor to control the temperature of the refrigerator.
Practical Implications
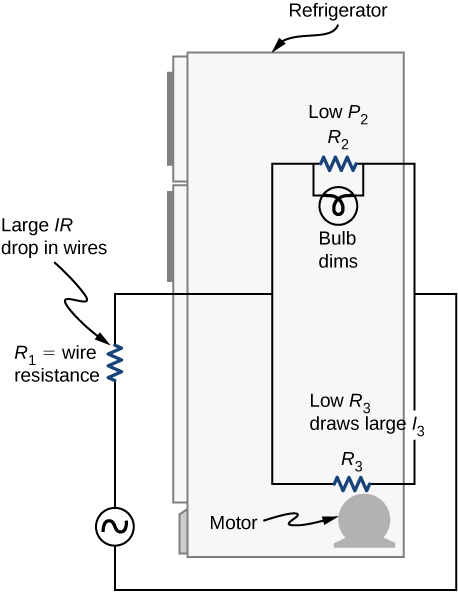
One implication of this last example is that resistance in wires reduces the current and power delivered to a resistor. If wire resistance is relatively large, as in a worn (or a very long) extension cord, then this loss can be significant. If a large current is drawn, the IR drop in the wires can also be significant and may become apparent from the heat generated in the cord.
For example, when you are rummaging in the refrigerator and the motor comes on, the refrigerator light dims momentarily. Similarly, you can see the passenger compartment light dim when you start the engine of your car (although this may be due to resistance inside the battery itself).
What is happening in these high-current situations is illustrated in Figure \(\PageIndex{7}\). The device represented by \(R_3\) has a very low resistance, so when it is switched on, a large current flows. This increased current causes a larger IR drop in the wires represented by \(R_1\), reducing the voltage across the light bulb (which is \(R_2\)), which then dims noticeably.
- Draw a clear circuit diagram, labeling all resistors and voltage sources. This step includes a list of the known values for the problem, since they are labeled in your circuit diagram.
- Identify exactly what needs to be determined in the problem (identify the unknowns). A written list is useful.
- Determine whether resistors are in series, parallel, or a combination of both series and parallel. Examine the circuit diagram to make this assessment. Resistors are in series if the same current must pass sequentially through them.
- Use the appropriate list of major features for series or parallel connections to solve for the unknowns. There is one list for series and another for parallel.
- Check to see whether the answers are reasonable and consistent.
Two resistors connected in series \((R_1, \, R_2)\) are connected to two resistors that are connected in parallel \((R_3, \, R_4)\). The series-parallel combination is connected to a battery. Each resistor has a resistance of 10.00 Ohms. The wires connecting the resistors and battery have negligible resistance. A current of 2.00 Amps runs through resistor \(R_1\). What is the voltage supplied by the voltage source?
Strategy
Use the steps in the preceding problem-solving strategy to find the solution for this example.
Solution
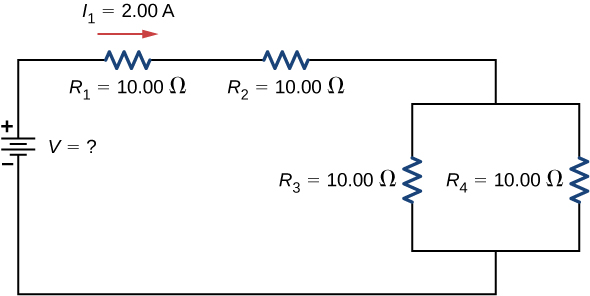
- Draw a clear circuit diagram (Figure \(\PageIndex{8}\)).
- The unknown is the voltage of the battery. In order to find the voltage supplied by the battery, the equivalent resistance must be found.
- In this circuit, we already know that the resistors \(R_1\) and \(R_2\) are in series and the resistors \(R_3\) and \(R_4\) are in parallel. The equivalent resistance of the parallel configuration of the resistors \(R_3\) and \(R_4\) is in series with the series configuration of resistors \(R_1\) and \(R_2\).
- The voltage supplied by the battery can be found by multiplying the current from the battery and the equivalent resistance of the circuit. The current from the battery is equal to the current through \(R_1\) and is equal to 2.00 A. We need to find the equivalent resistance by reducing the circuit. To reduce the circuit, first consider the two resistors in parallel. The equivalent resistance is \[R_{34} = \left(\frac{1}{10.00 \, \Omega} + \frac{1}{10.00 \, \Omega}\right)^{-1} = 5.00 \, \Omega. \nonumber\] This parallel combination is in series with the other two resistors, so the equivalent resistance of the circuit is \(R_{eq} = R_1 + R_2 + R_{34} = (25.00 \, \Omega\). The voltage supplied by the battery is therefore \(V = IR_{eq} = 2.00 \, A (25.00 \, \Omega) = 50.00 \, V\).
- One way to check the consistency of your results is to calculate the power supplied by the battery and the power dissipated by the resistors. The power supplied by the battery is \(P_{batt} = IV = 100.00 \, W\).
Since they are in series, the current through \(R_2\) equals the current through \(R_1\). Since \(R_3 = R_4\), the current through each will be 1.00 Amps. The power dissipated by the resistors is equal to the sum of the power dissipated by each resistor:
\[\begin{align*} P &= I_1^2R_1 + I_2^2R_2 + I_3^2R_3 + I_4^2R_4 \\[4pt] &= 40.00 \, W + 40.00 \, W + 10.00 \, W + 10.00 \, W = 100. \, W. \end{align*}\]
Since the power dissipated by the resistors equals the power supplied by the battery, our solution seems consistent.
Significance
If a problem has a combination of series and parallel, as in this example, it can be reduced in steps by using the preceding problem-solving strategy and by considering individual groups of series or parallel connections. When finding \(R_{eq}\) for a parallel connection, the reciprocal must be taken with care. In addition, units and numerical results must be reasonable. Equivalent series resistance should be greater, whereas equivalent parallel resistance should be smaller, for example. Power should be greater for the same devices in parallel compared with series, and so on.


