6.3: Explaining Gauss’s Law
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of this section, you will be able to:
- State Gauss’s law
- Explain the conditions under which Gauss’s law may be used
- Apply Gauss’s law in appropriate systems
We can now determine the electric flux through an arbitrary closed surface due to an arbitrary charge distribution. We found that if a closed surface does not have any charge inside where an electric field line can terminate, then any electric field line entering the surface at one point must necessarily exit at some other point of the surface. Therefore, if a closed surface does not have any charges inside the enclosed volume, then the electric flux through the surface is zero. Now, what happens to the electric flux if there are some charges inside the enclosed volume? Gauss’s law gives a quantitative answer to this question.
To get a feel for what to expect, let’s calculate the electric flux through a spherical surface around a positive point charge q, since we already know the electric field in such a situation. Recall that when we place the point charge at the origin of a coordinate system, the electric field at a point P that is at a distance r from the charge at the origin is given by
\vec{E}_p = \dfrac{1}{4\pi \epsilon_0}\dfrac{q}{r^2}\hat{r}, \nonumber
where \hat{r} is the radial vector from the charge at the origin to the point P. We can use this electric field to find the flux through the spherical surface of radius r, as shown in Figure \PageIndex{1}.
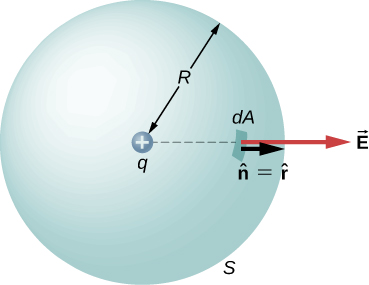
Then we apply \Phi = \int_S \vec{E} \cdot \hat{n} dA to this system and substitute known values. On the sphere, \hat{n} and r = R so for an infinitesimal area dA,
\begin{align*} d\Phi &= \vec{E} \cdot \hat{n} dA \\[4pt] &= \dfrac{1}{4\pi \epsilon_0} \dfrac{q}{R^2} \hat{r} \cdot \hat{r} dA \\[4pt] &= \dfrac{1}{4\pi \epsilon_0} \dfrac{q}{R^2} dA. \end{align*}
We now find the net flux by integrating this flux over the surface of the sphere:
\Phi = \dfrac{1}{4\pi \epsilon_0} \dfrac{q}{R^2} \oint_S dA = \dfrac{1}{4\pi \epsilon_0} \dfrac{q}{R^2} (4\pi R^2) = \dfrac{q}{\epsilon_0}. \nonumber
where the total surface area of the spherical surface is 4\pi R^2. This gives the flux through the closed spherical surface at radius r as
\Phi = \dfrac{q}{\epsilon_0}. \nonumber
A remarkable fact about this equation is that the flux is independent of the size of the spherical surface. This can be directly attributed to the fact that the electric field of a point charge decreases as 1/r^2 with distance, which just cancels the r^2 rate of increase of the surface area.
Electric Field Lines Picture
An alternative way to see why the flux through a closed spherical surface is independent of the radius of the surface is to look at the electric field lines. Note that every field line from q that pierces the surface at radius R_1 also pierces the surface at R_2 (Figure \PageIndex{2}).
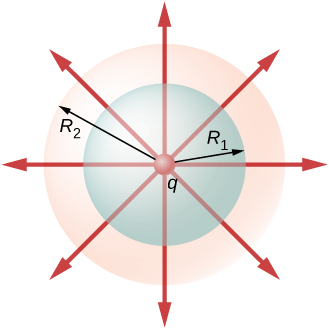
Therefore, the net number of electric field lines passing through the two surfaces from the inside to outside direction is equal. This net number of electric field lines, which is obtained by subtracting the number of lines in the direction from outside to inside from the number of lines in the direction from inside to outside gives a visual measure of the electric flux through the surfaces.
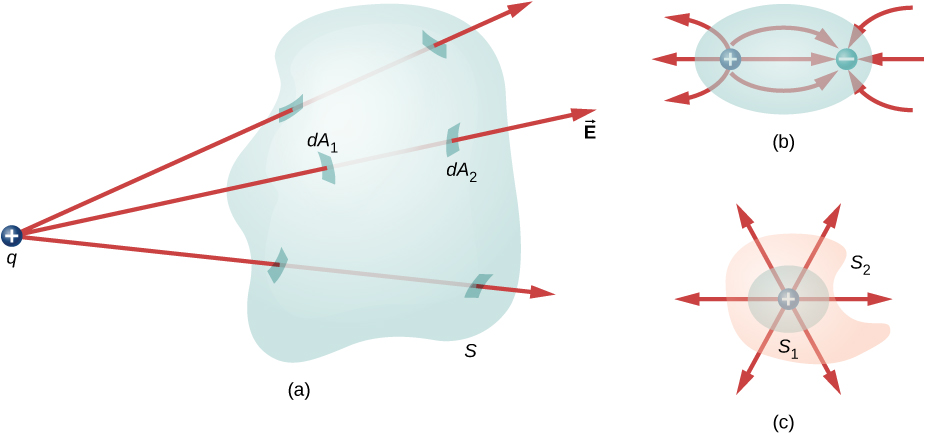
You can see that if no charges are included within a closed surface, then the electric flux through it must be zero. A typical field line enters the surface at dA_1 and leaves at dA_2. Every line that enters the surface must also leave that surface. Hence the net “flow” of the field lines into or out of the surface is zero (Figure \PageIndex{3a}). The same thing happens if charges of equal and opposite sign are included inside the closed surface, so that the total charge included is zero (Figure \PageIndex{3b}). A surface that includes the same amount of charge has the same number of field lines crossing it, regardless of the shape or size of the surface, as long as the surface encloses the same amount of charge (Figure \PageIndex{3c}).
Statement of Gauss’s Law
Gauss’s law generalizes this result to the case of any number of charges and any location of the charges in the space inside the closed surface. According to Gauss’s law, the flux of the electric field \vec{E} through any closed surface, also called a Gaussian surface, is equal to the net charge enclosed (q_{enc}) divided by the permittivity of free space (\epsilon_0):
\Phi_{\text{Closed Surface}} = \dfrac{q_{enc}}{\epsilon_0}. \nonumber
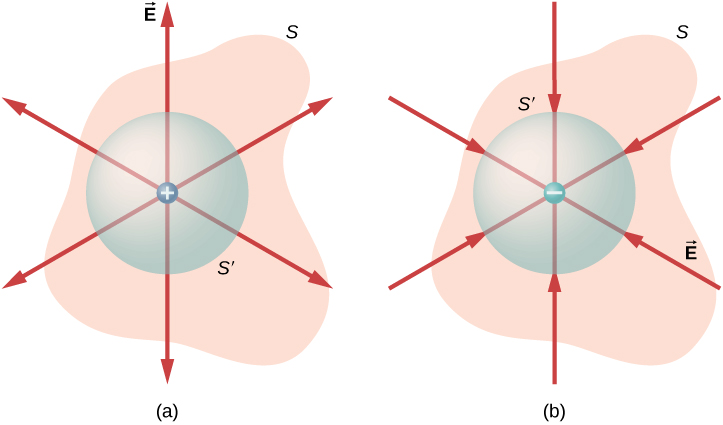
This equation holds for charges of either sign, because we define the area vector of a closed surface to point outward. If the enclosed charge is negative (Figure \PageIndex{4b}), then the flux through either S or S' is negative.
The Gaussian surface does not need to correspond to a real, physical object; indeed, it rarely will. It is a mathematical construct that may be of any shape, provided that it is closed. However, since our goal is to integrate the flux over it, we tend to choose shapes that are highly symmetrical.
If the charges are discrete point charges, then we just add them. If the charge is described by a continuous distribution, then we need to integrate appropriately to find the total charge that resides inside the enclosed volume. For example, the flux through the Gaussian surface S of Figure \PageIndex{5} is
\Phi = (q_1 + q_2 + q_5)/\epsilon_0. \nonumber
Note that q_{enc} is simply the sum of the point charges. If the charge distribution were continuous, we would need to integrate appropriately to compute the total charge within the Gaussian surface.
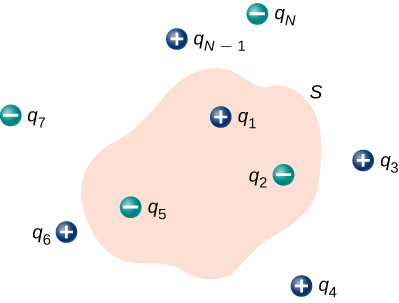
Recall that the principle of superposition holds for the electric field. Therefore, the total electric field at any point, including those on the chosen Gaussian surface, is the sum of all the electric fields present at this point. This allows us to write Gauss’s law in terms of the total electric field.
The flux \Phi of the electric field \vec{E} through any closed surface S (a Gaussian surface) is equal to the net charge enclosed (q_{enc}) divided by the permittivity of free space (\epsilon_0):
\Phi = \oint_S \vec{E} \cdot \hat{n} dA = \dfrac{q_{enc}}{\epsilon_0}. \nonumber
To use Gauss’s law effectively, you must have a clear understanding of what each term in the equation represents. The field \vec{E} is the total electric field at every point on the Gaussian surface. This total field includes contributions from charges both inside and outside the Gaussian surface. However, q_{enc} is just the charge inside the Gaussian surface. Finally, the Gaussian surface is any closed surface in space. That surface can coincide with the actual surface of a conductor, or it can be an imaginary geometric surface. The only requirement imposed on a Gaussian surface is that it be closed (Figure \PageIndex{5}).
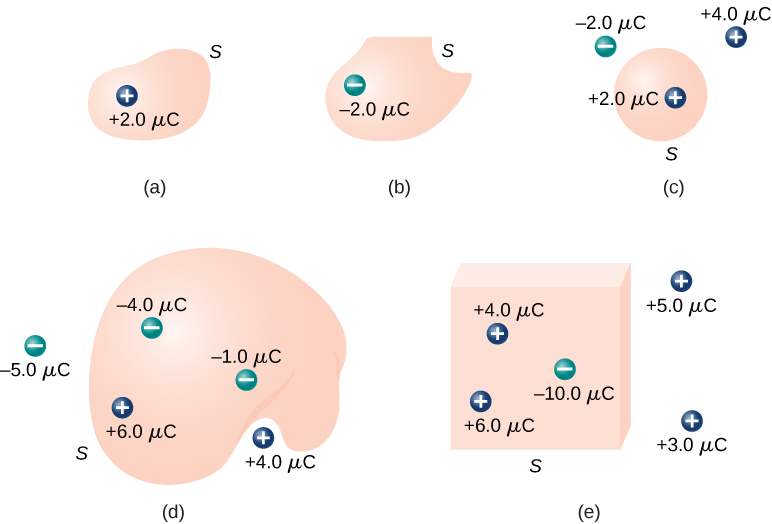
Calculate the electric flux through each Gaussian surface shown in Figure \PageIndex{7}.
Strategy
From Gauss’s law, the flux through each surface is given by q_{enc}/\epsilon_0, where q_{enc} is the charge enclosed by that surface.
Solution
For the surfaces and charges shown, we find
a. \Phi = \frac{2.0 \, \mu\mathrm{C}}{\epsilon_0} = 2.3 \times 10^5\, \mathrm{N} \cdot \mathrm{m}^2/\mathrm{C}.
b. \Phi = \frac{-2.0 \, \mu\mathrm{C}}{\epsilon_0} = -2.3 \times 10^5\, \mathrm{N} \cdot \mathrm{m}^2/\mathrm{C}.
c. \Phi = \frac{2.0 \, \mu\mathrm{C}}{\epsilon_0} = 2.3 \times 10^5\, \mathrm{N} \cdot \mathrm{m}^2/\mathrm{C}.
d. \Phi = \frac{-4.0 \, \mu\mathrm{C} + 6.0 \, \mu\mathrm{C} - 1.0 \, \mu\mathrm{C}}{\epsilon_0} = 1.1 \times 10^5\, \mathrm{N} \cdot \mathrm{m}^2/\mathrm{C}.
e. \Phi = \frac{4.0 \, \mu\mathrm{C} + 6.0 \, \mu\mathrm{C} - 10.0 \, \mu\mathrm{C}}{\epsilon_0} = 0.
Significance
In the special case of a closed surface, the flux calculations become a sum of charges. In the next section, this will allow us to work with more complex systems.
Calculate the electric flux through the closed cubical surface for each charge distribution shown in Figure \PageIndex{8}.
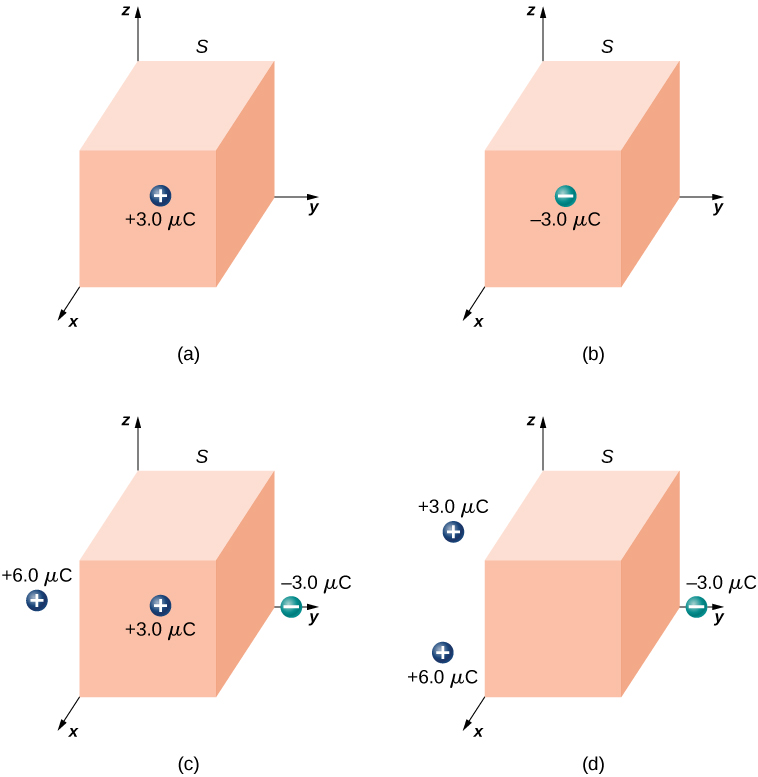
- Answer a
-
3.4 \times 10^5 \,\mathrm{N} \cdot \mathrm{m}^2/\mathrm{C}
- Answer b
-
-3.4 \times 10^5 \,\mathrm{N} \cdot \mathrm{m}^2/\mathrm{C}
- Answer c
-
3.4 \times 10^5 \,\mathrm{N} \cdot \mathrm{m}^2/\mathrm{C}
- Answer d
-
0
Use this simulation to adjust the magnitude of the charge and the radius of the Gaussian surface around it. See how this affects the total flux and the magnitude of the electric field at the Gaussian surface.


