3.1: Inertia
( \newcommand{\kernel}{\mathrm{null}\,}\)
In everyday language, we speak of something or someone “having a large inertia” to mean, essentially, that they are very difficult to set in motion. This usage of the word “inertia” is consistent with the “law of inertia” we introduced in the previous chapter (which states, among other things, that an object at rest, if left to itself, will just remain at rest), but it goes a bit beyond that by trying to quantify just how hard it may be to get the object to move.
We do know, from experience, that lighter objects are easier to set in motion than heavier objects, but most of us probably have an intuition that gravity (the force that pulls an object towards the earth and hence determines its weight) is not involved in an essential way here. Imagine, for instance, the difference between slapping a volleyball and a bowling ball. It is not hard to believe that the latter would hurt as much if we did it while floating in free fall in the space station (in a state of effective “weightlessness”) as if we did it right here on the surface of the earth. In other words, it is not (necessarily) how heavy something feels, but just how massive it is.
But just what is this “massiveness” quality that we associate intuitively with a large inertia? Is there a way (other than resorting to the weight again) to assign to it a numerical value?
Relative Inertia and Collisions
One possible way to determine the relative inertias of two objects, conceptually, at least, is to try to use one of them to set the other one in motion. Most of us are familiar with what happens when two identical objects (presumably, therefore, having the same inertia) collide: if the collision is head-on (so the motion, before and after, is confined to a straight line), they basically exchange velocities. For instance, a billiard ball hitting another one will stop dead and the second one will set off with the same speed as the first one. The toy sometimes called “Newton’s balls” or “Newton’s cradle” also shows this effect. Intuitively, we understand that what it takes to stop the first ball is exactly the same as it would take to set the second one in motion with the same velocity.
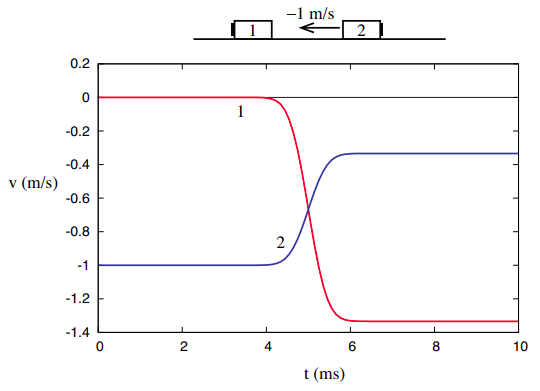
But what if the objects colliding have different inertias? We expect that the change in their velocities as a result of the collision will be different: the velocity of the object with the largest inertia will not change very much, and conversely, the change in the velocity of the object with the smallest inertia will be comparatively larger. A velocity vs. time graph for the two objects might look somewhat like the one sketched in Figure 3.1.1.
In this picture, object 1, initially moving with velocity v1i = 1 m/s, collides with object 2, initially at rest. After the collision, which here is assumed to take a millisecond or so, object 1 actually bounces back, so its final velocity is v1f = −1/3 m/s, whereas object 2 ends up moving to the right with velocity v2f = 2/3 m/s. So the change in the velocity of object 1 is Δv1=v1f−v1i = −4/3 m/s, whereas for object 2 we have Δv2=v2f−v2i = 2/3 m/s.
It is tempting to use this ratio, Δv1/Δv2, as a measure of the relative inertia of the two objects, only we’d want to use it upside down and with the opposite sign: that is, since Δv2/Δv1 = −1/2 we would say that object 2 has twice the inertia of object 1. But then we have to ask: is this a reliable, repeatable measure? Will it work for any kind of collision (within reason, of course: we clearly need to stay in one dimension, and eliminate external influences such as friction), and for any initial velocity?
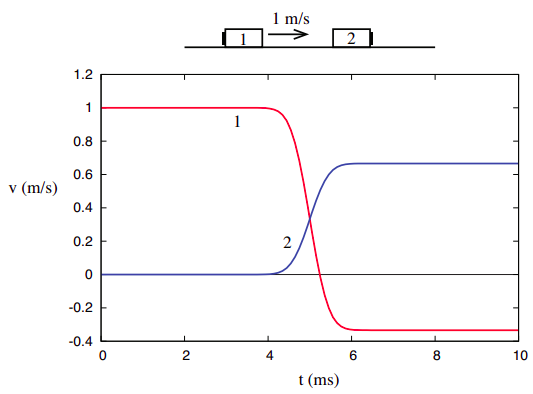
To begin with, we have reason to expect that it does not matter whether we shoot object 1 towards object 2 or object 2 towards object 1, because we learned in the previous chapter that only relative motion is detectable, and the relative motion is the same in both cases. Consider, for instance, what the collision in Figure 3.1.1 appears like to a hypothetical observer moving along with object 1, at 1 m/s. To him, object 1 appears to be at rest, and it is object 2 that is coming towards him, with a velocity of −1 m/s. To see what the outcome of the collision looks like to him, just add the same −1 m/s to the final velocities we obtained before: object 1 will end up moving at v1f = −4/3 m/s, and object 2 would move at v2f = −1/3 m/s, and we would have a situation like the one shown in Figure 3.1.2, where both curves have simply been shifted down by 1 m/s:
Figure 3.1.2: Another example (really the same collision as in Figure 3.1.1, only as seen by an observer initially moving to the right at 1 m/s).
But then, this is exactly what we should expect to find also in our laboratory if we actually did send the second object at 1 m/s towards the first one sitting at rest. All the individual velocities have changed relative to Figure 3.1.1, but the velocity changes, Δv1 and Δv2, are clearly still the same, and therefore so is our (tentative) measure of the objects’ relative inertia.
Clearly, the same argument can be used to conclude that the same result will be obtained when both objects are initially moving towards each other, as long as their relative velocity is the same as in these examples, namely, 1 m/s. However, unless we do the experiments we cannot really predict what will happen if we increase (or decrease) their relative velocity. In fact, we could imagine smashing the two objects at very high speed, so they might even become seriously mangled in the process. Yet, experimentally (and this is not at all an obvious result!), we would still find the same value of −1/2 for the ratio Δv2/Δv1, at least as long as the collision is not so violent that the objects actually break up into pieces.
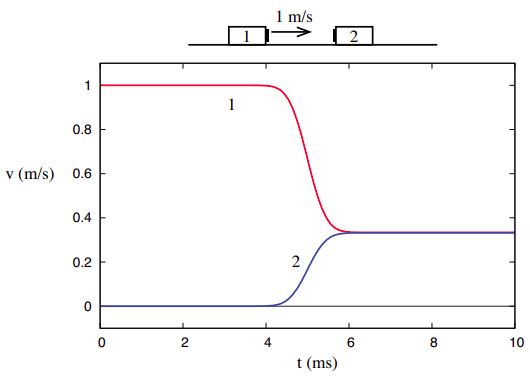
Perhaps the most surprising result of our experiments would be the following: imagine that the objects have a “sticky” side (for instance, the small black rectangles shown in the pictures could be strips of Velcro), and we turn them around so that when they collide they will end up stuck to each other. In this case (which, as we shall see later, is termed a completely inelastic collision), the v-vs-t graph might look like Figure 3.1.3 below.
Now the two objects end up moving together to the right, fairly slowly: v1f=v2f = 1/3 m/s. The velocity changes are Δv1 = −2/3 m/s and Δv2 = 1/3 m/s, both of which are different from what they were before, in Figs. 3.1.1 and 3.1.2: yet, the ratio Δv2/Δv1 is still equal to −1/2, just as in all the previous cases.
Inertial Mass: Definition and Properties
At this point, it would seem reasonable to assume that this ratio, Δv2/Δv1, is, in fact, telling us something about an intrinsic property of the two objects, what we have called above their “relative inertia.” It is easy, then, to see how one could assign a value to the inertia of any object (at least, conceptually): choose a “standard” object, and decide, arbitrarily, that its inertia will have the numerical value of 1, in whichever units you choose for it (these units will turn out, in fact, to be kilograms, as you will see in a minute). Then, to determine the inertia of another object, which we will label with the subscript 1, just arrange a one-dimensional collision between object 1 and the standard, under the right conditions (basically, no net external forces), measure the velocity changes Δv1 and Δvs, and take the quantity −Δvs/Δv1 as the numerical value of the ratio of the inertia of object 1 to the inertia of the standard object. In symbols, using the letter m to represent an object’s inertia,
m1ms=−ΔvsΔv1
But, since ms = 1 by definition, this gives us directly the numerical value of m1.
The reason we use the letter m is, as you must have guessed, because, in fact, the inertia defined in this way turns out to be identical to what we have traditionally called “mass.” More precisely, the quantity defined this way is an object’s inertial mass. The remarkable fact, mentioned earlier, that the force of gravity between two objects turns out to be proportional to their inertial masses, allows us to determine the inertial mass of an object by the more traditional procedure of simply weighing it, rather than elaborately staging a collision between it and the standard kilogram on an ice-hockey rink. But, in principle, we could conceive of the existence of two different quantities that should be called “inertial mass” and “gravitational mass,” and the identity (or more precisely, the—so far as we know—exact proportionality) of the two is a rather mysterious experimental fact1.
In any case, by the way we have constructed it, the inertial mass, defined as in Equation (???), does capture, in a quantitative way, the concept that we were trying to express at the beginning of the chapter: namely, how difficult it may be to set an object in motion. In principle, however, other experiments would need to be conducted to make sure that it does have the properties we have traditionally associated with the concept of mass. For instance, suppose we join together two objects of mass m. Is the mass of the resulting object 2m? Collision experiments would, indeed, show this to be the case with great accuracy in the macroscopic world (with which we are concerned this semester), but this is a good example of how you cannot take anything for granted: at the microscopic level, it is again a fact that the inertial mass of an atomic nucleus is a little less than the sum of the masses of all its constituent protons and neutrons2.
Probably the last thing that would need to be checked is that the ratio of inertias is independent of the standard. Suppose that we have two objects, to which we have assigned masses m1 and m2 by arranging for each to collide with the “standard object” independently. If we now arrange for a collision between objects 1 and 2 directly, will we actually find that the ratio of their velocity changes is given by the ratio of the separately determined masses m1 and m2? We certainly would need that to be the case, in order for the concept of inertia to be truly useful; but again, we should not assume anything until we have tested it! Fortunately, the tests would indeed reveal that, in every case, the expected relationship holds3
At this point, we are not just in possession of a useful definition of inertia, but also of a veritable law of nature, as I will explain next.
1This fact, elevated to the category of a principle by Einstein (the equivalence principle) is the starting point of the general theory of relativity.
2And this is not just an unimportant bit of trivia: all of nuclear power depends on this small difference.
3Equation ??? actually is found to hold also at the microscopic (or quantum) level, although there we prefer to state the result by saying that conservation of momentum holds (see the following section).