10.5: Advanced Topics
( \newcommand{\kernel}{\mathrm{null}\,}\)
Tidal Forces
Throughout this chapter we have treated the objects interacting gravitationally as if they were particles, that is to say, as if they were non-deformable and their shape and relative orientation did not matter. However, these conditions are never quite realized in real life. Some planets, like our own Earth, are particularly susceptible to deformation, because of the large amount of fluid matter on their surface, and even rocky planets and moons are sensitive to tidal forces, which are the differences on the gravitational pull by the central attractor on different parts of the object considered.
If you look back on Figure 10.1.1, for instance, it is easy to see that the moon must be pulling more strongly on the side of the Earth that is closer to it (the left side, on that picture) than on the farther side. This is, of course, because the force of gravity depends on the distance between the interacting objects, and is stronger when the objects are closer. You can easily calculate that the force by the moon on a given volume of Earth (say, a cubic meter) is about 7% stronger on the near side than on the far side. A deformable object subject to such a pair of forces will naturally be stretched along the direction of the pull: in the case of the Earth, this “stretching” affects primarily the water in the oceans that cover most of the surface, resulting in two “tidal bulges” that account for the well-known phenomenon of tides: as the earth rotates around its axis, each point on the surface passes through one of the bulges once a day, resulting in two high tides each day (and, in between, a comparatively lower water level, or low tide, twice a day as well).5
For many objects in the solar system, this tidal stretching has, over millions of years, resulted in a permanent deformation. The tidal forces by the Earth on the moon are weaker than those by the moon on the Earth (since the moon is much smaller, the difference between the Earth’s pull on the moon’s near and far side is less than 1.5%), but at a time when the moon was more malleable than at present, it was enough to produce an elongation along the Earth-moon axis that is now pretty much frozen in place.
Once a satellite (I will use the term generically to refer either to a planet orbiting the sun, or a moon orbiting a planet) becomes permanently deformed, a new phenomenon, known as tidal locking, can happen. Suppose the satellite is rotating around its own axis, in addition to orbiting around the primary body. As you can see from the figure below, if the rotation is too fast, the gravitational forces from the primary will result in a net torque on the satellite that will tend to slow down its rotation; conversely, if it is rotating too slowly, the torque will tend to speed up the rotation. A torque-free situation will only happen when the satellite’s period of rotation exactly matches its orbital period, so that it always shows the same side to the primary body. This is the situation with the Earth’s moon, and indeed for most of the major moons of the giant planets.
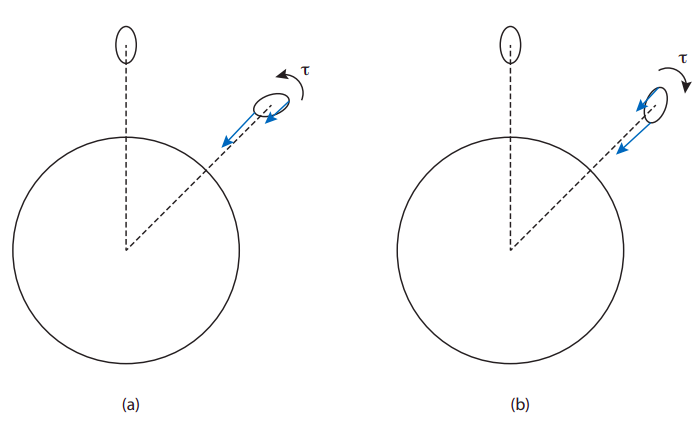
Note that, by the same argument, we would expect the tidal forces on the Earth due to the moon to try and bring the Earth into tidal locking with the moon—that is, to try to bring the duration of an Earth day closer to that of a lunar month. Indeed, the moon’s tidal forces have been slowing down the Earth’s rotation for billions of years now, and continue to do so by about 15 microseconds every year. This process requires dissipation of energy, (which is in fact associated with the ocean tides: think of the frictional forces caused by the waves, as the tide comes in and out); however, to the extent that the Earth-moon system may be treated as isolated, its total angular momentum cannot change, and so the slowing-down of the Earth is accompanied by a very gradual increase in the radius of the moon’s orbit—about 3.8 cm per year, currently—to keep the total angular momentum constant.
5You may ask, besides being stretched, shouldn’t the net pull of the moon cause the Earth to fall towards it? The answer is that the Earth does not fall straight towards the moon, for the same reason the moon does not fall straight towards the Earth: both have a sideways velocity that keeps them in a steady orbit, for which the net gravitational pull provides the centripetal force. Both actually orbit around the center of mass of the system, which is located about 1,690 km under the Earth’s surface; the Earth’s orbit (and its orbital velocity) is much smaller than the moon’s, by virtue of its much larger mass, of course.


