3.1.2: A Few Other Examples of Resonance
( \newcommand{\kernel}{\mathrm{null}\,}\)
Resonance can occur in any system that has a natural frequency. You probably have experienced a rattle or buzz in your car that only occurs at a certain speed. This is an example of resonance; the tires provide a periodic driving force which changes frequency as you change speed. Various parts of the car have different natural frequencies, particularly parts that have come loose. If the driving frequency of the rotating tires matches the natural frequency these parts will vibrate at a larger amplitude, making a buzz or rattle. Here are some other examples.
Video/audio examples:
- Helicopter ground resonance. What is the driving force in this case?
- Bridge resonances: bouncing, twisting, Tacoma Narrows, Russian bridge.
- Breaking glass: 1, 2. What are the driving forces in these two cases? [NOTE: Don't do this at home! The breaking glass can go into your eyes or mouth.]
- More Singing rod. What is the driving force that makes the rod resonate?
- A web page with more examples of resonance.
- A description of building resonance as a result of a dance class.
You probably have blown across the top of a bottle to get a note. Different sized bottles make different notes and partially filling the bottles with water also changes the pitch. These are examples of Helmholtz resonators; a container of gas with a single opening that will resonate at a specific pitch. Blowing across the top causes a driving force on the air inside which has a natural frequency due to the 'springiness' of the air and the size of the container. As we will see, acoustic stringed instruments such as the guitar consist of a hollow body which acts like a Helmholtz resonator. Here are more details on Helmholtz resonance.
If you have ever been annoyed by a low frequency sound while driving down the highway with one window partially open, you were experiencing a Helmholtz resonance where the air blowing past the open window caused the air inside the car to vibrate.
Resonance also occurs in electrical circuits. In fact this is one way a radio receiver can tune to a certain broadcast frequency. The parameters of the circuit are adjusted so that the circuit has a resonance equal to the frequency of the station you are trying to listen to. With those parameters the circuit has much more current flowing for that particular frequency, thus making current flow for that frequency much larger than any other frequency. Here is a circuit simulation that shows three circuits. The top circuit is being driven below resonance so the current flow is small. The bottom circuit has a driving frequency that is too large. The middle circuit is driven at the resonance frequency of 41.1 Hz and has the largest current oscillations.
You may have heard the word resonance applied in the medical world. Magnetic Resonance Imaging (MRI) is used in medicine to get images inside the body without doing harm to the living tissue. Every different molecule in the body has a different natural frequency of oscillation. Each molecule also has electrical charges on them so that they can be driven by an oscillating magnetic and electric field (an electromagnetic wave). When the driving frequency of the oscillating magnetic field equals the natural frequency of the molecule, the molecule absorbs the energy and undergoes larger oscillations. This absorbed energy doesn't pass through the body and so is not detected outside after the magnetic field passes through. By changing the driving frequency (the frequency of the electromagnetic wave) it is possible to map the location of different types of molecules in the body, giving a map of the internal structures. This tutorial on MRI gives more details and shows some pictures generated using magnetic resonance imaging.
Questions on Resonance:
- What is meant by damped harmonic motion? Give an example.
- What is meant by driven, damped harmonic motion? Give an example.
- What is the difference between natural frequency and driving frequency?
- Define resonance.
- List as many examples of resonance in every day life as you can think of.
- In the YouTube of the singer who broke a wine glass using his voice, explain why the wine glass broke.
- What is a Helmholtz resonator? Give an example.
- In the simulation with several different masses, explain why different masses resonate at different driving frequencies.
- The natural frequency of an oscillating object is 10 Hz. At what frequency would you want push it in order to make the oscillations bigger?
- For the previous question, how often in seconds should you push the object to make the oscillations bigger?
- State two ways to change the resonance frequency of a mass-spring system.
- Why does the amplitude of the driving force not matter as much as the frequency of the driving force?
- In the YouTube video with three different masses attached to rods on the cart, why are there three different resonance frequencies?
- Suppose you recorded the amplitude of a driven spring system for many different driving frequencies and got the following graph of amplitude versus driving frequency. According to the graph, what is the resonance frequency of the system?
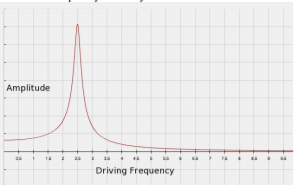
Figure 3.1.2.1
- What is the resonance frequency of a kid on a swing if the period of oscillation is 2.4 s?
- If the period of oscillation of a kid on a swing is 3.0 seconds you could push it with a period of 3.0 s and the oscillations would get larger. What would happen if instead you pushed every 6.0 s?
- For the 3.0 s oscillation in the previous question, what period other than 6.0 s could you push the swing so as to make the oscillation larger? We will talk about these higher frequencies (called harmonics) later.
- What would be best for a stringed instrument: a high Q-factor or a low one? Explain.
- In this chapter, you learned that a radio can be tuned to different frequencies by the principle of resonance. Would a higher Q-factor be beneficial for tuning a radio? Why or why not?
- Why does changing the driving force, Fo, not change the resonance frequency (Hint: Look at the equation for the resonance amplitude in the simulation exercise.)?


