5.1.1: Speeds of Different Types of Waves
( \newcommand{\kernel}{\mathrm{null}\,}\)
The speed of a wave is fixed by the type of wave and the physical properties of the medium in which it travels. An exception is electromagnetic waves which can travel through a vacuum. For most substances the material will vibrate obeying a Hooke's law force as a wave passes through it and the speed will not depend on frequency. Electromagnetic waves in a vacuum and waves traveling though a linear medium are termed linear waves and have constant speed. Examples:
- For sound waves in a fluid (for example air or water) the speed is determined by v=(B/ρ)1/2 where B is the bulk modulus or compressibility of the fluid in newtons per meter squared and ρ is the density in kilograms per cubic meter.
- For sound waves in a solid the speed is determined by v=(Y/ρ)1/2 where Y is Young's modulus or stiffness in Newtons per meter squared and ρ is the density in kilograms per meter cubed.
- For waves on a string the speed is determined by v=(T/μ)1/2 where T is the tension in the string in Newtons and μ is the mass per length in kilograms per meter.
- Although electromagnetic waves do not need a medium to travel (they can travel through a vacuum) their speed in a vacuum, c=(1/μoεo)1/2=3.0×108 m/s is governed by two physical constants, the permeability μo and the permittivity, εo of free space (vacuum).
| Speed of Sound in Various Substances (CRC Handbook) | ||
|---|---|---|
| Glasses (0∘C) | Substance | Speed of Sound (m/s) |
| Carbon Dioxide | 259 | |
| Hydrogen | 1284 | |
| Helium | 965 | |
| Nitrogen | 334 | |
| Oxygen | 316 | |
| Air (21% Oxygen, 78% Nitrogen) | 331 | |
| Air (20∘C) | 344 | |
| Liquids (25∘C) | Glycerol | 1904 |
| Sea Water (3.5% salinity) | 1535 | |
| Water | 1493 | |
| Mercury | 1450 | |
| Kerosene | 1324 | |
| Methyl Alcohol | 1103 | |
| Carbon Tetrachloride | 926 | |
| Solids | Diamond | 12000 |
| Pyrex Glass | 5640 | |
| Iron | 5960 | |
| Granite | 6000 | |
| Aluminum | 5100 | |
| Brass | 4700 | |
| Copper (annealed) | 4760 | |
| Gold | 3240 | |
| Lead (annealed) | 2160 | |
| Rubber (gum) | 1550 | |
Table 5.1.1.1
Here is a more comprehensive list of the speed of sound in various materials.
As we saw in the previous chapter, there is a relationship between the period, wavelength and speed of the wave. The period of a cork floating in the water is affected by how fast the wave passes (wave speed) and the distance between peaks (wavelength). The relationship between speed, period and wavelength of a sine wave is given by v=λ/T where wavelength and period for a sine wave were defined previously. This can also be written as v=λf since frequency is the inverse of period and is true for all linear waves. Notice that, since wave speed is normally a fixed quantity the frequency and wavelength will be inversely proportion; higher frequencies mean shorter wavelengths.
Often it is easier to write ω=2πf where ω is the angular frequency in radians per second instead of having to write 2πf everywhere. Likewise it is easier to write k=2π/λ where k is the wave number in radians per meter rather than having to write 2π/λ a lot. (Note that k is not a spring constant here.) Using these new definitions the speed of a wave can also be written as v=fλ=ω/k.
If the medium is uniform the speed of a wave is fixed and does not change. There are circumstances where the speed of a particular wave does change, however. Notice that the speed of sound in air depends on the density of the air (mass per volume). But the density of air changes with temperature and humidity. So the speed of sound can be different on different days and in different locations. The temperature dependence of the speed of sound in air is given by v=344+0.6(T−20) in meters per second where T is the temperature in Celsius (T here is temperature, not period). Notice that at room temperature (20∘C) sound travels at 344 m/s.
The speed of sound can also be affected by the movement of the medium in which it travels. For example, wind can carry sound waves further (i.e. faster) if the sound is traveling in the same direction or it can slow the sound down if the sound is traveling in a direction opposite to the wind direction.
Electromagnetic waves travel at c=3.0×108 m/s in a vacuum but slow down when they pass through a medium (for example light passing from air to glass). This occurs because the material has a different value for the permittivity and/or permeability due to the interaction of the wave with the atoms of the material. The amount the speed changes is given by the index of refraction n=c/v where c is the speed of light in a vacuum and v is the speed in the medium. The frequency of the wave does not change when it slows down so, since v=λf, the wavelength of electromagnetic waves in a medium must be slightly smaller.
Video/audio examples:
- What is the speed of sound in a vacuum? Buzzer in a bell jar. Why is there no sound when the air is removed from the jar?
- Demonstration of speed of sound in different gasses. Why is there no sound when the air is removed from the jar?
- These two videos demonstrate the Allasonic effect. The speed of sound is different in a liquid with air bubbles because the density is different. As the bubbles burst, the speed of sound changes, causing the frequency of sound waves in the liquid column to change, thus changing the pitch. Example: one, two. What do you hear in each case?
- The Zube Tube is a toy that has a spring inside attached to two plastic cups on either end. Vibrations in the spring travel at different speeds so a sound starting at one end (for example a click when you shake the tube and the spring hits the cup) ends up changing pitch at the other end as the various frequencies arrive. In other words this is a nonlinear system. See if you can figure out from the video which frequencies travel faster, high frequencies or low.
Mini-lab on measuring the speed of sound.
Questions on Wave Speed:
f=1/T,v=fλ,v=ω/k,k=2π/λ,ω=2πf,y(x,t)=Acos(kx−ωt+ϕ),v=√B/Q
- Light travels at 3.0×108 m/s but sound waves travel at about 344 m/s. What is the time delay for light and sound to arrive from a source that is 10,000 m away (this can be used to get an approximate distance to a thunderstorm)?
- What two mistakes are made in science fiction movies where you see and hear an explosion in space at the same time?
- Consult the table for the speed of sound in various substances. If you have one ear in the water and one ear out while swimming in a lake and a bell is rung that is half way in the water some distance away, which ear hears the sound first?
- At 20C the speed of sound is 344 m/s. How far does sound travel in 1 s? How far does sound travel in 60 s?
- Compare the last two answers with the distance traveled by light which has a speed of 3.0×108 m/s. Why do you see something happen before you hear it?
- The speed of sound in water is 1482 m/s. How far does sound travel under water in 1 s? How far does sound travel under water in 60 s?
- What happens to the speed of sound in air as temperature increases?
- Using the equation for the speed of sound at different temperatures, what is the speed of sound on a hot day when the temperature is 30∘C? Hint: v=344 m/s+0.6(T−20) where T is the temperature in Celsius.
- Using the speed of sound at 30∘C from the last question, recalculate the distance traveled for the cases in question four.
- Suppose on a cold day the temperature is −10∘C(14∘F). You are playing in the marching band outside. How long does it take the sound from the band to reach the spectators if they are 100 m away?
- What is the difference in the speed of sound in air on a hot day (40∘C) and a cold day (0∘C)?
- What would an orchestra sound like if different instruments produced sounds that traveled at different speeds?
- The speed of a wave is fixed by the medium it travels in so, for a given situation, is usually constant. What happens to the frequency of a wave if the wavelength is doubled?
- What happens to the wavelength of a wave if the frequency is doubled and has the same speed?
- Suppose a sound wave has a frequency 200 Hz. If the speed of sound is 343 m/s, what wavelength is this wave?
- What factors determine the speed of sound in air?
- Why do sound waves travel faster through liquids than air?
- Why do sound waves travel faster through solids than liquids?
- The speed of sound in a fluid is given by v=√B/Q where B is the Bulk Modulus (compressibility) and Q is the density. What happens to the speed if the density of the fluid increases?
- What must be true about the compressibility, B, of water versus air, given that sound travels faster in water and water is denser than air?
- The speed of sound in a fluid is given by v=√B/Q where B is the Bulk Modulus (compressibility) and Q is the density. Can you think of a clever way to measure the Bulk Modulus of a fluid if you had an easy way to measure the speed of sound in a fluid? Explain.
- The speed of sound on a string is given by v=√T/μ where T is the tension in Newtons and μ is the linear density (thickness) in kg/m. You also know that v=fλ. Give two ways of changing the frequency of vibration of a guitar string based on the knowledge of these two equations.
- For the previous question, increasing the tension does what to the frequency? What does using a denser string do to the frequency?
- The following graph is of a wave, frozen in time at t=0. The equation describing the wave is y(x,t)=Acos(kx−ωt+ϕ). Sketch the effect of doubling the amplitude, A.
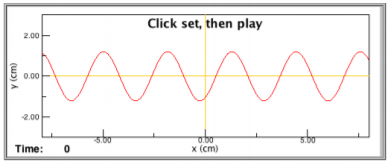
Figure 5.1.1.1
- For the following graph of a wave, sketch the effect of doubling the wavelength.
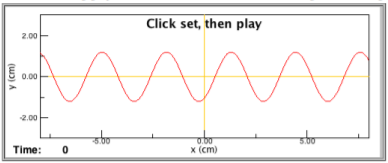
Figure 5.1.1.2
- The mathematical description of a sine wave is given by y(x,t)=Acos(kx−ωt+ϕ). Explain what each of the terms (A,k,ω,ϕ) represent.


