6.2.1: Reflection
( \newcommand{\kernel}{\mathrm{null}\,}\)
In many cases waves of all types will travel in a straight line, reflecting off of objects and surfaces at the same angle that they strike the surface. This is called the law of reflection and is true for sound waves as well as light as long as the surface is smooth relative to the wavelength. In the pictures below the arrows show the direction the light or sound is traveling. On the left for reflection off a smooth flat surface the angle of incidence, θi equals the angle of reflection, θr.
The law is still obeyed for a smooth curved surface but with a different result as shown in the figure on the right. In this case rays starting from one special point called the focal point still obey the law of reflection but they end up traveling outward parallel to each other. If we reverse the rays they will arrive parallel but all reflect through the focal point. Flashlights have curved mirrors behind the bulb with the bulb at the focal point so that the light coming from the flashlight is approximately a parallel beam. Outdoor concert shells are often built with a curved shape with the performer located at the focal point. This is so the sound is directed outward and spread evenly in the direction of the audience.
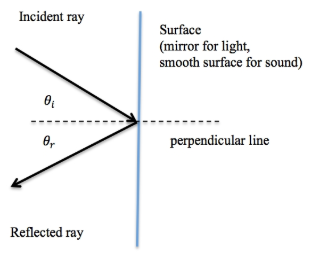
Figure 6.2.1.1
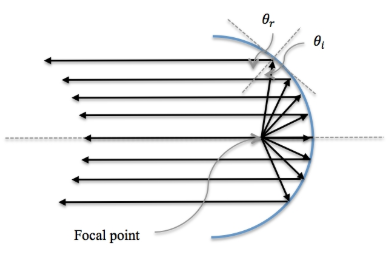
Figure 6.2.1.2
In the two pictures below the blue lines give the direction the wave is traveling and the small gray lines represent the crests of the waves (so the distance between the gray lines is the wavelength). For specular reflection (picture on the left) the surface is smooth relative to the size of the wave and the entire wave obeys the law of reflection. For diffuse reflection (picture on the right) the surface is rough relative to the size of the wave and, while individual components of the wave obeys the law of reflection, the wave as a whole is broken up by the reflection. To avoid strong echoes and other unwanted acoustic effects, surfaces in concert halls are designed to absorb sound and also to reflect sound diffusely, as we will see later.
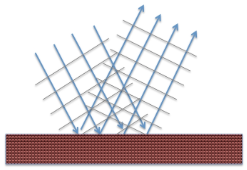
Figure 6.2.1.3

Figure 6.2.1.4
Video/audio examples:
- Reflection of light.
- Ripple tank reflection of water waves.
- This Ripple Tank simulation by Paul Falstad lets you look at wave reflection from a parabolic mirror and inside a circular or elliptic enclosure. Directions: Choose Setup: Parabolic Mirror 1, Mirror 2, Circle or Ellipse. Describe what you see in each case. For the ellipse, what happens to sound that starts at the focus of an elliptical chamber? This is the explanation behind the strange acoustics in some large building such as the nation's capital.
- Animation of what images look like in a convex mirror.


