6.3: Chapter Checklist

Learning Objectives

You should now be able to:

1. Take the limit of a space translation invariant discrete system as the distance between the parts goes to zero, interpret the physics of the resulting continuous system, and find its dispersion relation;
2. Use the Fourier series to set up and solve the initial value problem for a massive string with various boundary conditions.

Problems

6.1. Consider the continuous string of (6.7)-(6.10) as the continuum limit of a beaded string with \(W\) beads as \(W \rightarrow \infty\). Write the analog of (6.8) and (6.10) for finite \(W\). Show that the limit as \(W \rightarrow \infty\) yields (6.10). Hint: This is an exercise in the definition of an integral as the limit of a sum. But to do the first part, you will either need to use normal coordinates, X or prove the identity

\[\begin{aligned}
\sum_{k=1}^{W} \sin \frac{n k \pi}{W+1} \sin \frac{n^{\prime} k \pi}{W+1} = \begin{cases}b & \text { if } n=n^{\prime} \neq 0 \\ 0 & \text { if } n \neq n^{\prime} \text { and } n, n^{\prime}>0\end{cases}
\end{aligned}\]

for a constant \(b\) and find \(b\).

6.2. Do the integrals in (6.20). Hint: Use integration by parts and watch for miraculous cancellations.

6.3. Find the normal modes of the string with two free ends, shown in Figure \( 6.7\).

6.4. Fun with Fourier Series and Fractals

In this problem you will explore the Fourier series for an interesting set of functions. Consider a function of the following form, defined on the interval [0,1]: \[f(t)=\sum_{j=0}^{\infty} h^{j} g\left(\operatorname{frac}\left(2^{j} t\right)\right) .\]

Figure \( 6.7\): A continuous string with both ends free to oscillate in the transverse direction.

where \[g(t)=\left\{\begin{array}{c}
1 \text { for } 0 \leq t \leq w \\
0 \text { for } w<t<1-w \\
1 \text { for } 1-w \leq t \leq 1
\end{array}\right.\]

and \(\operatorname{frac}(x)\) denotes the fractional part, i.e. \(\operatorname{frac}(4.39)=0.39\). \(f(t)\) thus depends on the two parameters \(h\) and \(w\), where \(0 < h < 1\) and \(0 < w < 1 / 2\). For example, for \(h = 1 / 2\) and \(w = 1 / 4\), the \(h^{0}\) term is shown in Figure \( 6.8.

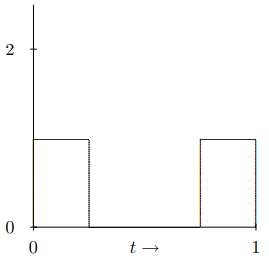
Figure \( 6.8\): The \(h^{0}\) term in \(f(t)\) for \(h = 1 / 2\) and \(w = 1 / 4\).

If we add in the \(h^{1}\) term we get the picture in Figure \( 6.9\).

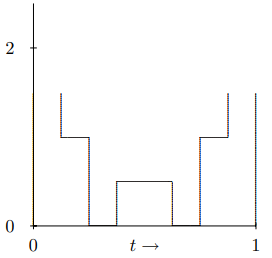
Figure \( 6.9\): The first two terms in \(f(t)\) for \(h = 1 / 2\) and \(w = 1 / 4\).

Adding the \(h^{2}\) term gives the picture in Figure \( 6.10\), and so on.

The final result is a very bumpy function, called a “fractal.” You cannot compute this function exactly, but you can include enough terms to get to any desired accuracy. Because

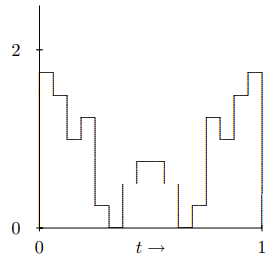
Figure \( 6.10\): The first three terms in \((f(t)\) for \(h = 1 / 2\) and \(w = 1 / 4\).

the function is symmetric about \(t = 1 / 2\), it is really only necessary to plot it from \(0\) to \(1 / 2\). Also because of the symmetry, it can be expressed in terms of a Fourier series of cosines, \[f(t)=\sum_{k=0}^{\infty} b_{k} \cos 2 \pi k t .\]

Show that the Fourier coefficients are given by \[b_{k}=\frac{2}{\pi k} \sum_{j=0}^{\xi(k)}(2 h)^{j} \sin \left(2 \pi k w / 2^{j}\right)\]

for \(k \neq 0\), and \[b_{0}=\frac{2 w}{1-h}\]

where the function, \(\xi(k)\) is the number of times 2 appears as a factor of \(k\). Thus \(\xi(0)=\xi(1)=\xi(3)=0, \xi(2)=1, \xi(4)=2,\) etc.

Write a program to display and print the fractal for some set of parameters, \(h\) and \(w\). Also, display the truncated Fourier series, \[f_{m}(t)=\sum_{k=0}^{m-1} b_{k} \cos 2 \pi k t\]

with m terms, for \(m = 5\), \(10\), and \(20\) (or more if you have a fast computer).