1.3: Working with Gravity: Potential Energy
- Page ID
- 1626
Gravitational Potential Energy near the Earth
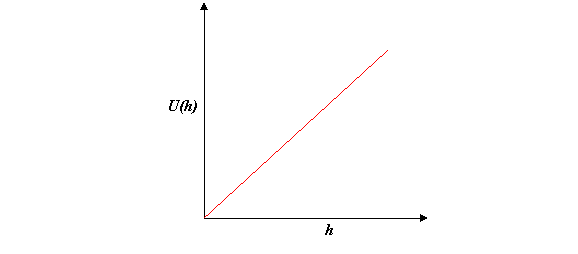
We first briefly review the familiar subject of gravitational potential energy near the Earth’s surface, such as in a room. The gravitational force is of course \( \vec F = m\vec g \) vertically downwards. To raise a mass m, we must apply an upward force \( -\vec F \), balancing gravity, so the net force on the body is zero and it can move upwards at a steady speed (ignoring air resistance, of course, and assuming we gave it a tiny extra push to get it going).
Applying the steady force \( -\vec F \) as the mass moves a small distance \( \bigtriangleup \vec r \) takes work \( -\vec F \cdot \bigtriangleup \vec r \), and to raise the mass m through a height h takes work mgh. This energy is stored and then, when the object falls, released as kinetic energy. For this reason it is called potential energy, being “potential kinetic energy”, and written
\[ U = U (h) = mgh \tag{1.3.1}\]
Note one obvious ambiguity in the definition of potential energy: do we measure h from the floor, from the top of our workbench, or what? That depends on how far we will allow the raised object to fall and convert its potential energy to kinetic energy—but the main point is it doesn’t matter where the zero is set, the quantity of physical interest is always a difference of potential energies between two heights—that’s how much kinetic energy is released when it falls from one height to the other. (Perhaps we should mention that some of this potential energy may go to another form of energy when the object falls—if there is substantial air resistance, for example, some could end up eventually as heat. We shall ignore that possibility for now.)
Onward and Upward
Let’s now consider the work involved in lifting something so high that the Earth’s gravitational pull becomes noticeably weaker.
It will still be true that lifting through \( \bigtriangleup \vec r \) takes work \( -\vec F \cdot \bigtriangleup \vec r \), but now \( \vec F( \vec r) = \frac {G}{Mmr^2} \), downwards. So
\[ dU = -\vec F \cdot d \vec r = \dfrac {GMm}{r^2} dr \tag{1.3.2}\]
and to find the total work needed to lift a mass m from the Earth’s surface (rE from the center of the Earth) to a point distance r from the center we need to do an integral:
\[ U(r) - U(r_E) = \int \limits_{r_E}^{r} \dfrac {GMm}{r^\prime 2}dr^ \prime = GMm \left( \dfrac {1}{r_E} - \dfrac {1}{r} \right) \tag{1.3.3} \] .
First check that this makes sense close to the Earth’s surface, that is, in a room. For this case, \[ r = r_E + h, \, where \, h \ll r_E \] .
Therefore
\[ U(r) - U(r_E) = GMm \left( \dfrac {1}{r_E} - \dfrac {1}{r} \right) \tag{1.3.4}\]
\[ = GMm \left( \dfrac {r_E + h - r_E}{r_E(r_E + h)} \right) \tag{1.3.5}\]
\[ = GMm \left( \dfrac {h}{r_E^2} \right) \] \[ = mgh \tag{1.3.6}\]
where the only approximation is to replace rE + h by rE in the denominator, giving an error of order h/rE, parts per million for an ordinary room.
To see what this potential function looks like on a larger scale, going far from the Earth, it is necessary first to decide where it is most natural to set it equal to zero. The standard convention is to set the potential energy equal to zero at r = infinity! The reason is that if two bodies are very far from each other, they have no influence on each other’s movements, so it is pointless to include a term in their total energy which depends on their mutual interaction.
Taking the potential energy zero at infinity gives the simple form \[U(r) = - \dfrac{GMm}{r} \tag {1.3.7}\]
we plot it below with r in units of Earth radii. The energy units are GMm/rE, the -1 at the far left being at the Earth’s surface (r = 1), and the first steep almost linear part corresponds to mgh.
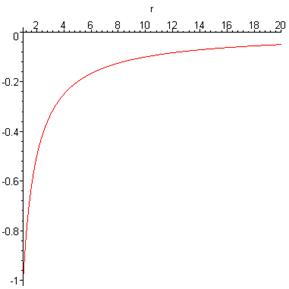
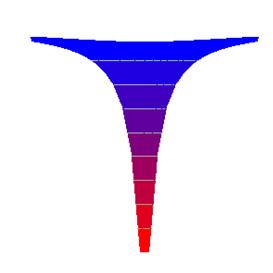
The above is a map of the potential energy “hill” to be climbed in going away from the Earth vertically upwards from any point. To gain something closer to a three-dimensional perspective, the Earth can be visualized as being at the bottom of a “potential well” with flared sides, like this:
Or, from a different perspective:
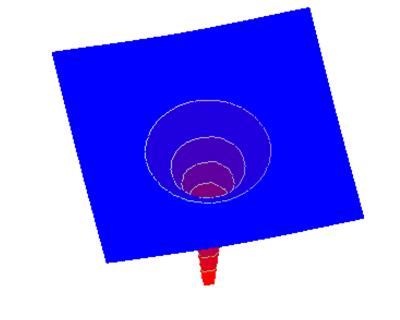
Of course, this is still only in two dimensions, but that’s fine for most gravitational problems: planetary orbits are only two-dimensional. A satellite in a circular orbit around the Earth can be imagined as a frictionless particle sliding around inside this “cone” at a fixed height, for an elliptic orbit the particle would slide between different heights.
Gravitational Potential Energy in a Two Body System
By this, I mean how do we extend the above picture of gravitational potential as a “well” going down out of a flat plane to, for example, the combined potential energies of a mass in the gravitational fields of both the Earth and the Moon, as would occur on a flight to the Moon.
From the beginning of the previous section, the potential energy difference between any two points from the gravitational force of a single body is the work done against that force in going from one point to the other, \[ U(\vec r_2) - U(\vec r_1) = - \int \limits_{\vec r_1}^{\vec r_2} \vec F \cdot d\vec r .\tag {1.3.8} \]
It doesn’t matter how the path gets from \( \vec r_1 \) to \( \vec r_2 \): if it took different amounts of work depending on the path, we could gain energy by having a mass go up one path and down the other, a perpetual motion machine. The fact that this is not true means the gravitational field is conservative: gravitational potential energy can b a term in a conservation of energy equation.
Recall from the previous lecture that the gravitational field obeys the Law of Superposition: to find the total gravitational force on a mass from the gravitational field of both the Earth and the Moon, we just add the vectors representing the separate forces. It follows immediately from this that, putting \( \vec F = \vec F_{earth} + \vec F_{moon} \), the gravitational potential energy difference between two points is simply the sum of the two terms.
From this, then, the potential energy of a mass somewhere between the Earth and the Moon is
\[ U_{total} (\vec r) = - \dfrac {GM_Em}{|\vec r - \vec r_{CE}|} - \dfrac {GM_Mm}{|\vec r - \vec r_{CM}|} \tag {1.3.9} \]
taking as usual \( U( \infty ) = 0 \), and \( \vec r_{CE}, \vec r_{CM} \) are the coordinates of the centers of the Earth and the Moon respectively.
It’s worth visualizing this combined potential: it would look like two of these cone-like wells, one much smaller than the other, in what is almost a plain. Going in a straight line from inside one well to the inside of the other would be uphill then downhill, and at the high point of the journey the potential energy would be flat, meaning that the gravitational pull of the Earth just cancels that of the Moon, so no work is being done in moving along the line at that point. The total potential energy there is still of course negative, that is, below the value (zero) far away in the plain.
Gravitational Potential
The gravitational potential is defined as the gravitational potential energy per unit mass, and is often written \( \phi (\vec r ) \). We shall rarely use it—the problems we encounter involve the potential energy of a given mass m. (But \( \phi (\vec r ) \) is a valuable concept in more advanced treatments. It is analogous to the electrostatic potential, and away from masses obeys the same partial differential equation, \( \nabla^2 (\vec r ) = 0 \).)
Escape!
How fast must a rocket be moving as it escapes the atmosphere for it to escape entirely from the Earth’s gravitational field? This is the famous escape velocity, and, neglecting the depth of the atmosphere, it clearly needs sufficient initial kinetic energy to climb all the way up the hill, \[ \dfrac {1}{2} m \nu_{escape}^2 = \dfrac {GMm}{r_E}, \, \nu_{escape} = \sqrt {\dfrac {2GM}{r_E}} \tag{1.3.10} \]
This works out to be about 11.2 km per sec. For the Moon, escape velocity is only 2.3 km per second, and this is the reason the Moon has no atmosphere: if it had one initially, the Sun’s heat would have been sufficient to give the molecules enough thermal kinetic energy to escape. In an atmosphere in thermal equilibrium, all the molecules have on average the same kinetic energy. This means lighter molecules on average move faster. On Earth, any hydrogen or helium in the atmosphere would eventually escape for the same reason.
Exercise \(\PageIndex{1}\)
Saturn’s moon Titan is the same size as our Moon, but Titan has a thick atmosphere. Why?
Exercise \(\PageIndex{2}\)
Imagine a tunnel bored straight through the Earth emerging at the opposite side of the globe. The gravitational force in the tunnel is \( F = \dfrac {mgr}{r_E} \), as derived above.
- Find an expression for the gravitational potential energy in the tunnel. Take it to be zero at the center of the Earth.
- Now sketch a graph of the potential energy as a function of distance from the Earth’s center, beginning at the center but continuing beyond the Earth’s radius to a point far away. This curve must be continuous. Conventionally, the potential energy is defined by requiring it to be zero at infinity. How would you adjust your answer to give this result?
Potential and Kinetic Energy in a Circular Orbit
The equation of motion for a satellite in a circular orbit is\[ \dfrac {mv^2}{r} = \dfrac {GMm}{r^2} \]
It follows immediately that the kinetic energy \[ K.E. = \dfrac {1}{2}mv^2 = \dfrac {1}{2} \dfrac {GMm}{r} = -\dfrac {1}{2} U(r) \], that is, the Kinetic Energy = -1/2 (Potential Energy) so the total energy in a circular orbit is half the potential energy.
The satellite’s motion can be visualized as circling around trapped in the circular potential “well” pictured above. How fast does move? It is easy to check that for this circular orbit
\[ \nu_{orbit} = \sqrt {\dfrac {GM}{r_{orbit}}}\]
Recalling that the escape velocity from this orbit is \( \nu_{escape} = \sqrt {\dfrac {2GM}{r_{orbit}}} \), we have \[ \nu_{escape} = \sqrt {2} \nu_{orbit} \] relating speed in a circular planetary orbit to the speed necessary, starting at that orbit, to escape completely from the sun’s gravitational field.
This result isn’t surprising: increasing the speed by \( \sqrt {2} \) doubles the kinetic energy, which would then exactly equal the potential energy: that means just enough kinetic energy for the satellite to climb the hill completely out of the “well”.
Bottom line: the total energy of a planet of mass m in a circular orbit of radius r about a Sun of mass M is
\[ E_{tot} = - \dfrac {GMm}{2r} \].
Contributors and Attributions
- Michael Fowler (Beams Professor, Department of Physics, University of Virginia)


