Frames of Reference and Newton’s Laws
- Page ID
- 317
The cornerstone of the theory of special relativity is the Principle of Relativity:
The Laws of Physics are the same in all inertial frames of reference.
We shall see that many surprising consequences follow from this innocuous looking statement.
Let us first, however, briefly review Newton’s mechanics in terms of frames of reference.
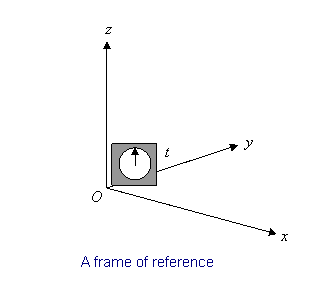
A “frame of reference” is just a set of coordinates: something you use to measure the things that matter in Newtonian problems, that is to say, positions and velocities, so we also need a clock.
A point in space is specified by its three coordinates (x, y, z) and an “event” like, say, a little explosion, by a place and time: (x, y, z, t).
An inertial frame is defined as one in which Newton’s law of inertia holds—that is, any body which isn’t being acted on by an outside force stays at rest if it is initially at rest, or continues to move at a constant velocity if that’s what it was doing to begin with. An example of a non-inertial frame is a rotating frame, such as a carousel.
The “laws of physics” we shall consider first are those of Newtonian mechanics, as expressed by Newton’s Laws of Motion, with gravitational forces and also contact forces from objects pushing against each other. For example, knowing the universal gravitational constant from experiment (and the masses involved), it is possible from Newton’s Second Law,
force = mass × acceleration,
to predict future planetary motions with great accuracy.
Suppose we know from experiment that these laws of mechanics are true in one frame of reference. How do they look in another frame, moving with respect to the first frame? To find out, we have to figure out how to get from position, velocity and acceleration in one frame to the corresponding quantities in the second frame.
Obviously, the two frames must have a constant relative velocity, otherwise the law of inertia won’t hold in both of them. Let’s choose the coordinates so that this velocity is along the x-axis of both of them.
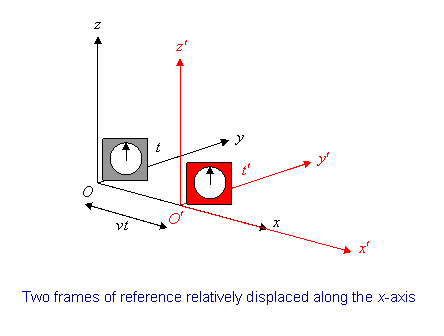
Notice we also throw in a clock with each frame.
Suppose S′ is proceeding relative to S at speed v along the x-axis. For convenience, let us label the moment when O′ passes O as the zero point of timekeeping.
Now what are the coordinates of the event (x, y, z, t) in S′? It’s easy to see t′ = t—we synchronized the clocks when O′ passed O. Also, evidently, y′ = y and z′ = z, from the figure. We can also see that x = x′ +vt. Thus (x, y, z, t) in S corresponds to (x′, y′, z′, t′ ) in S′, where
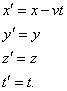
That’s how positions transform; these are known as the Galilean transformations.
What about velocities ? The velocity in S′ in the x′ direction
![]()
This is obvious anyway: it’s just the addition of velocities formula
![]()
How does acceleration transform?
![]()
since v is constant.
That is to say,
![]()
the acceleration is the same in both frames. This again is obvious—the acceleration is the rate of change of velocity, and the velocities of the same particle measured in the two frames differ by a constant factor-the relative velocity of the two frames.
If we now look at the motion under gravitational forces, for example,
![]()
we get the same law on going to another inertial frame because every term in the above equation stays the same.
Note that ![]() is the rate of change of momentum—this is the same in both frames. So, in a collision, say, if total momentum is conserved in one frame (the sum of individual rates of change of momentum is zero) the same is true in all inertial frames.
is the rate of change of momentum—this is the same in both frames. So, in a collision, say, if total momentum is conserved in one frame (the sum of individual rates of change of momentum is zero) the same is true in all inertial frames.
Contributors
- Michael Fowler (Beams Professor, Department of Physics, University of Virginia)


