GENERAL RELATIVITY - a primer

Gravity and Time

Consider three clocks. Clocks 1 and 2 are mounted on a rotating disk, with clock 1 exactly at the center, and clock 2 fixed on 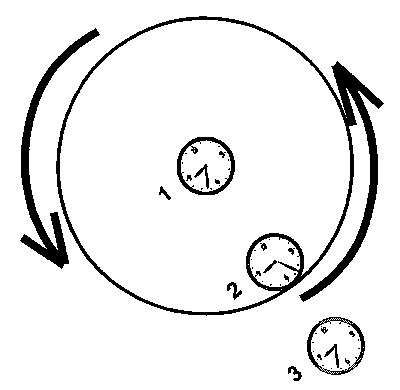the rim, and clock 3 is sitting at rest with respect to the centre of the disk. Note that the disk exerts a force on clock 2 which forces it to follow a circular path; since, without this force, clock 2 would move in a straight line, it is clear that the force and the resultant acceleration are both directed towards the centre of the disk. Clocks 1 and 3 are not moving relative to one another (there is some rotation involved, but their relative position in space does not change with time); thus, as far as Special Relativity is concerned, they keep the same time. However, clock 2 is moving with respect to clock 3; thus clock 2 is running slow as seen by clock 3. Since clocks 1 and 3 keep the same time, this means that clock 2 runs slow compared to clock 1, even though clocks 1 and 2 have no relative translatory motion. (Note that, since clock 2 is not in an inertial frame, Special Relativity does not make any statement about its timekeeping - this is a new effect). Finally, consider a clock situated on the disk somewhere between clocks 1 and 2; the acceleration of such a clock is less than that of clock 2, and since it is also moving more slowly than clock 2, it is running less slowly.

Generalising this result, we see that clocks undergoing acceleration will run slow compared to non-accelerating clocks; and the greater the acceleration, the greater will be this time dilation. Now according to the Equivalence Principle, an accelerating frame of reference cannot be distinguished from a frame in which there is a gravitational field. Thus the above result implies that clocks in a gravitational field run slow; and the greater the gravitational field, the greater the time dilation. Clocks on the ground floor of a tall building will run slower than those in the upper floors; if you want to keep (relatively) young, find a job in the basement - or become a miner!

Gravity and Space

Now consider the following: suppose we measure the circumference of the rotating disk. We could do this by laying a series of measuring rods along it. Relative to the centre of the disk, the measuring rods will appear contracted. Of course, if we measure the radius of the rotating disk, since the measuring rods are moving perpendicular to their length, there will be no length contraction. Thus the ratio of the circumference to the radius of a rotating disk (equal to 2 Pi in Euclidean geometry) will not be fixed, but will depend on the speed of rotation. By the Equivalence Principle, it is clear that measurements of distance will depend on the value of the local gravitational field, even if no relative motion is involved. The normal (Euclidean) geometry that we learnt at our mother's knee is no longer valid when strong gravitational fields are present. Gravity causes space to be non-Euclidean. The exact relationship between gravity and space is complicated. However it implies that the geometry of our universe is that of a curved, four dimensional space-time. Gravity is a manifestation of this space-time geometry; a gravitational field is nothing but the warping of this geometry. Mass causes the geometry to curve and warp, and the curvature is the gravitational field, which reveals itself as mass.

Bending of Light in a Gravitational Field.

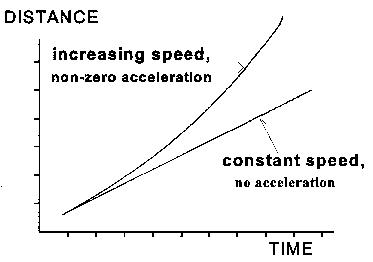
A brief review of the difference between constant speed and acceleration::

Something that moves with constant speed covers the same distance in every time interval; for instance a rocket travelling at one third the speed of light will cover 10 cm in 1 nanosecond. An accelerating rocket, on the other hand, will cover a distance that increases in each successive interval of time; e.g. in the first nanosecond it might cover 10cm, in the second 11cm, in the third 12 cm, in the fourth 13 cm, etc. The difference between the two cases is demonstrated in the graph.

Consider now what happens to a beam of light which is directed through the window of an accelerating rocket; suppose that 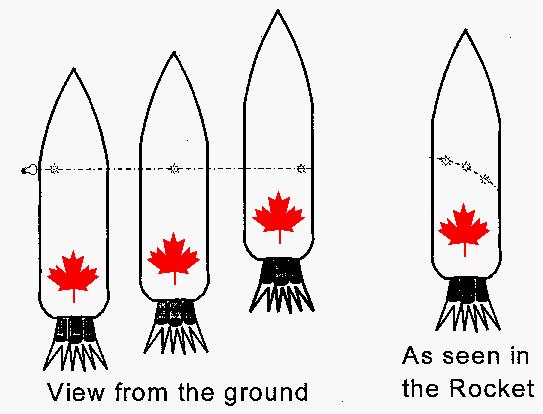both mission control (on the ground) and the astronauts (in the rocket) can observe the light at several points in its path (indicated on the diagram). Mission control will see the light beam moving in a straight path; however the astronauts in the rocket will detect the light at points which lie on a curve. (Note: it is instructive to consider what will happen if the rocket is simply moving with constant speed relative to mission control; a little thought should convince you that the light will move in a straight line in both frames). Thus, by the Principle of Equivalence, since an accelerating frame looks the same as a frame in a gravitational field, light appears to bend in a gravitational field. According to our new understanding of General Relativity, we interpret this to mean that light follows the quickest (or "straightest") path in curved space-time; this path is called a geodesic.

Experimental Verification.

By now, there have been very many quite precise verifications of the predictions of the General Theory of Relativity, and a full coverage of these would take many pages. However, to give you the flavour of the sorts of tests which are possible, I mention below some of the first - and therefore most exciting - experiments that have been done.

I. The Bending of Light

A) The General Theory predicts that light is bent by a gravitational field. In fact such an effect is also predicted by Newtonian theory and the of the deflection of light passing close to the sun was done as early as 1801, by considering the effect that Newtonian gravity would have on an object passing close to the sun with the speed of light. The prediction of General Relativity yields a value that is twice as large as the classical calculation.

To observe this effect, Eddington, in 1919 measured the apparent displacement of the distant stars as their light passed close to the sun; of course the stars can�t normally be seen when the sun is shining, so Eddington had to wait for a total eclipse of the sun. The amount a body moving at the speed of light would deflect is calculated to be 0.84 seconds of arc using Newtonian mechanics; the prediction of General Relativity is 1.74 seconds of arc. Eddington confirmed the latter value to within 20%, and later measurements made in a similar manner now give agreement to within 0.1%.

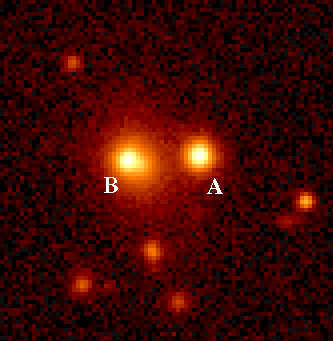
B) The observation of very distant objects can be distorted by the bending of light if the light from them passes close to a large mass, such as a galaxy. In this case the galaxy acts as a lens would, and multiple images of the distant object may be observed. In some cases the light from the distant object is shaped into a ring, called an Einstein ring. Several observations of such gravitational lensing have been observed; several beautiful examples are shown here.

This is one of the first multiply-imaged sources discovered in 1979 (by Walsh, Carswell and Weymann). Points A and B are images of the same distant source (quasar 0957+561), produced by light bending round a closer massive object that produces no image on this photograph.

This is one of the first so-called 'giant arcs', C12244-02, viewed by the Hubble Space Telescope.

In this case the foreground galaxy, shown by the bright spot at the center of the picture is so perfectly aligned with the distant galaxy that the image of the latter becomes an almost perfect Einstein Ring. This picture was taken using the Hubble Space Telescope, by J.L. King, University of Manchester.

II. Time Dilation - or the Gravitational Redshift

Both Special and General Relativity predict the slowing down of clocks under certain circumstances, and experiments to test the predictions of either theory must take account of the predictions of the other, since the effects of both theories are often present. Most General Relativity tests use atomic clocks that emit gamma or X-rays at specific frequencies; these frequencies provide the time scale. General Relativity predicts that clocks in greater gravitational fields will run more slowly than those in weaker gravitational fields; thus an atomic clock in a higher gravitational field will emit light of a lower frequency compared to a clock in a lower gravitational field. Since lower frequencies correspond to longer wavelengths and, for visible light, shifts to the red part of the spectrum, the effect predicted by the General Relativity is usually called the Gravitational Redshift.

A) In 1959 Pound and Rebka placed an atomic clock at the top of a seven storey office building at Harvard University and compared its frequency with that of a similar clock placed in the basement. Using an effect named after the German physicist, Mossbauer, they confirmed the prediction of General Relativity to within 1%. More recent experiments along these lines have improved the precision to 0.02%.

B) In 1971 Hafele and Keating tested relativistic predictions by comparing the time measured on an atomic clock flown around the world on commercial airlines to that of a stay-at-home clock. Here both General and Special Relativity come into play.

Lets consider first the effects of Special Relativity. As seen by a distant observer at rest with respect to the center of the earth, the clock at rest on the earth will run slow. If the other clock is placed in a plane flying Eastwards, its speed will add to that of the Earths rotation (which is in an Easterly direction; remember that the planes speed is relative to the atmosphere which moves with the Earth). Thus Special Relativity predicts that the flying clock will run slower than the stay-at-home clock, since it is moving faster. However, for a clock flying Westwards, its speed will subtract from that of the Earth, and it will gain time on the stay-at-home clock.

For General Relativity, however, the speed of the plane is irrelevant. The sole effect is due to gravity, and since the plane will experience less gravity when it is 10,000 metres in the air, the flying clock will always gain time compared to the clock on the ground.

The Hafele and Keating found that the flying clock lost (59+/-10) nanoseconds when flying East and gained (273+/-7) nanoseconds when flying West. It can be seen that their measurements agree well (within statistics) with the predictions.

THEORY	EFFECT	EASTWARDS flight (nanoseconds)	WESTWARDS flight (nanoseconds)
General Relativity	Gravity	144	179
Special Relativity	Kinematic	-184	96
Sum of Both	Net	-40+/-23	275+/-21

III. Other Tests

There have been many other successful tests of General Relativity. However the following two were among the first to truly establish the theory, and are good examples of later, more precise tests.

A) The Perihelion of Mercury. As you know, planets move in ellipses around the sun. However due to the influence of other planets their orbits are not quite closed; their perihelions (the line between the sun and the point of closest approach of the planet) will not be stationary in space but moved around the sun in a motion called precession. There is a contribution to this precession predicted by General Relativity. Mercury, the planet nearest the sun, should show this effect most of all, since it experiences the greatest gravitational effect. Indeed the Newtonian calculations of the perturbing effects of the other planets account for only 531 out of the observed 574 seconds of arc per century; General Relativity has to be invoked to explain the remaining 43 seconds.

B) Gravitational Waves. When a mass moves, it causes "ripples" in curved space-time as the geometry changes to accommodate the movement of the mass. (Think of the motion of the surface of your waterbed when you change position!). Remember what happens when we move a charge; electromagnetic waves are emitted. In just the same way, we expect that gravitational waves may be produced by accelerating masses, though the effect is very weak. For example, gravitational waves should be emitted by stars that are orbiting each other; the energy carried off by the waves will cause the orbiting bodies to lose kinetic energy, and the time for each orbit will gradually decrease (remember classical physics expected just such an effect for an electron orbiting a nucleus; it took Quantum Mechanics to explain why this didn't happen).

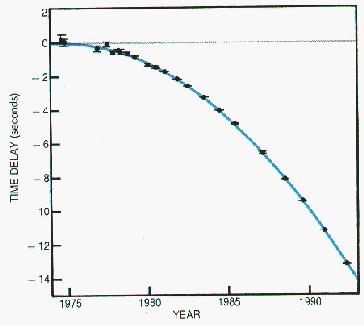Such an orbiting star has been identified - the binary pulsar PSR 1913+16) and the measured decrease in its period caused by the emission of gravitational wave energy agrees exactly with the calculations of General Relativity for this case. This is strong evidence for the existence of gravitational waves. The results of Taylor and Hulse, shown at right, won them the Nobel Prize for 1993: the blue curve is the time delay caused by the loss of energy by gravitational radiation, calculated from General Relativity, knowing the measured properties of the binary pulsar.
A large effort is currently being mounted in the US to detect the arrival of gravitational waves on earth; LIGO (the Large Interferometer Gravitational wave Observatory) will be operational by the end of the decade.