1.9.2: Triangles
( \newcommand{\kernel}{\mathrm{null}\,}\)
Triangles
- Identify equilateral, isosceles, scalene, acute, right, and obtuse triangles.
- Identify whether triangles are similar, congruent, or neither.
- Identify corresponding sides of congruent and similar triangles.
- Find the missing measurements in a pair of similar triangles.
- Solve application problems involving similar triangles
- Use the Pythagorean Theorem to find the unknown side of a right triangle.
- Solve application problems involving the Pythagorean Theorem.
Classifying and Naming Triangles
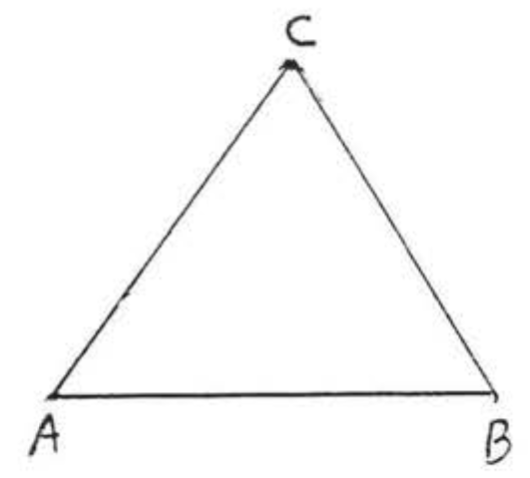
A triangle is formed when three straight line segments bound a portion of the plane. The line segments are called the sides of the triangle. A point where two sides meet is called a vertex of the triangle, and the angle formed is called an angle of the triangle. The symbol for triangle is △.
The triangle in Figure 1.9.2.1 is denoted by △ABC (or △BCA or △CAB, etc.).
- Its sides are AB, AC, and BC.
- Its vertices are A,B, and C.
- Its angles are ∠A, ∠B, and ∠C.
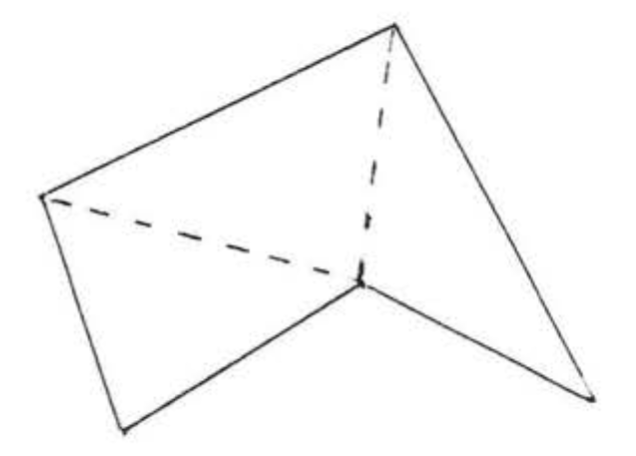
The triangle is the most important figure in plane geometry, This is because figures with more than three sides can always be divided into triangles (Figure 1.9.2.2). If we know the properties of a triangle, we can extend this knowledge to the study of other figures as well.
A fundamental property of triangles is the following:
The sum of the angles of a triangle is 180∘.
In △ABC of Figure 1.9.2.1, ∠A+∠B+∠C=180∘.
Find ∠C:
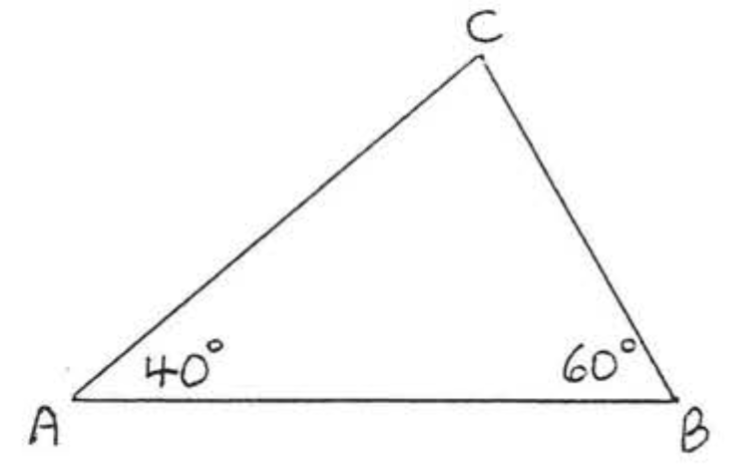
- Solution
-
∠A+∠B+∠C=180∘40∘+60∘+∠C=180∘100∘+∠C=180∘∠C=180∘−100∘∠C=80∘
Answer: ∠C=80∘
The table below shows and describes three classifications of triangles. Notice how the types of angles in the triangle are used to classify the triangle.
| Name of Triangle | Picture of Triangle | Description |
| Acute Triangle |  |
A triangle with 3 acute angles (3 angles measuring between 0° and 90°). |
| Obtuse Triangle | 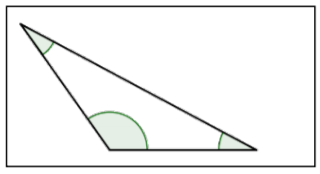 |
A triangle with 1 obtuse angle (1 angle measuring between 90° and 180°). |
| Right Triangle | 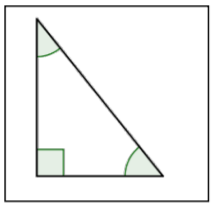 |
A triangle containing one right angle (1 angle that measures 90°). Note that the right angle is shown with a corner mark and does not need to be labeled 90°. |
The sum of the measures of the three interior angles of a triangle is always 180°. This fact can be applied to find the measure of the third angle of a triangle, if you are given the other two. Consider the examples below.
A triangle has two angles that measure 35° and 75°. Find the measure of the third angle.
- Solution
-
The sum of the three interior angles of a triangle is 180°.
35° + 75° + x = 180°
Find the value of x.
110º + x = 180º
x = 180° ‒ 110º
x = 70°
Answer: The third angle of the triangle measures 70°.
One of the angles in a right triangle measures 57º. Find the measurement of the third angle.
- Solution
-
The sum of the three angles of a triangle is 180°. One of the angles has a measure of 90° as it is a right triangle.
57° + 90° + x = 180°
Simplify.
147º + x = 180°
Find the value of x.
x = 180º - 147º
x = 33º
Answer: The third angle of the right triangle measures 33°.
There is an established convention for naming triangles. The labels of the vertices of the triangle, which are generally capital letters, are used to name a triangle.
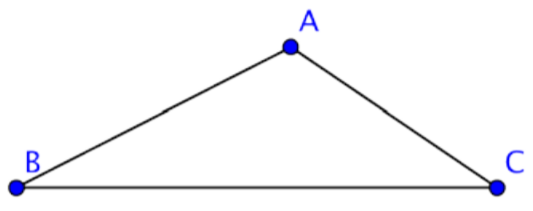
You can call this triangle ABC or ∆ABC since A, B, and C are vertices of the triangle. When naming the triangle, you can begin with any vertex. Then keep the letters in order as you go around the polygon. The triangle above could be named in a variety of ways: ∆ABC, or ∆CBA. The sides of the triangle are line segments AB, AC, and CB.
Just as triangles can be classified as acute, obtuse, or right based on their angles, they can also be classified by the length of their sides. Sides of equal length are called congruent sides. While we designate a segment joining points A and B by the notation ¯AB, we designate the length of a segment joining points A and B by the notation AB without a segment bar over it. The length AB is a number, and the segment ¯AB is the collection of points that make up the segment.
Mathematicians show congruency by putting a hash mark symbol through the middle of sides of equal length. If the hash mark is the same on one or more sides, then those sides are congruent. If the sides have different hash marks, they are not congruent. The table below shows the classification of triangles by their side lengths.
| Name of Triangle | Picture of Triangle | Description |
| Equilateral Triangle | 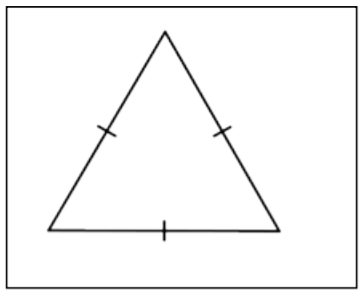 |
A triangle whose three sides have the same length. These sides of equal length are called congruent sides. |
| Isosceles Triangle | 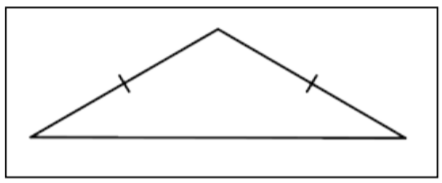 |
A triangle with exactly two congruent sides. |
| Scalene Triangle | 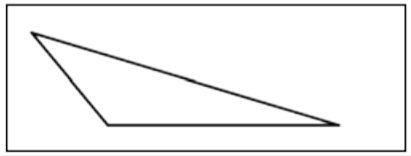 |
A triangle in which all three sides are a different length. |
To describe a triangle even more specifically, you can use information about both its sides and its angles. Consider this example.
Classify the triangle below.
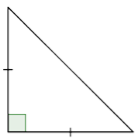
- Solution
-
Notice what kind of angles the triangle has. Since one angle is a right angle, this is a right triangle.
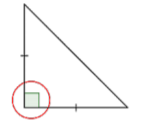
Notice the lengths of the sides. Are there congruence marks or other labels?
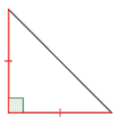
The congruence marks tell us there are two sides of equal length. So, this is an isosceles triangle.
Answer: This is an isosceles right triangle
Find y and x:
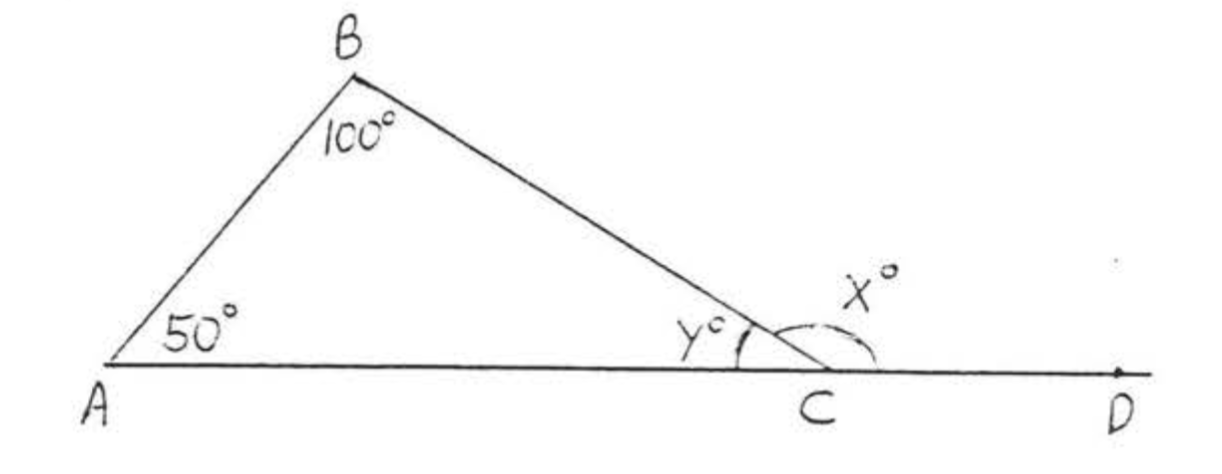
- Solution
-
50+100+y=180150+y=180y=180−150y=30x=180−30=150
Answer: y=30, x=150.
In Figure 1.9.2.3, ∠x is called an exterior angle of △ABC, ∠A, ∠B, and ∠y are called the interior angles of △ABC. ∠A and ∠B are said to be the interior angles remote from the exterior angle ∠x.
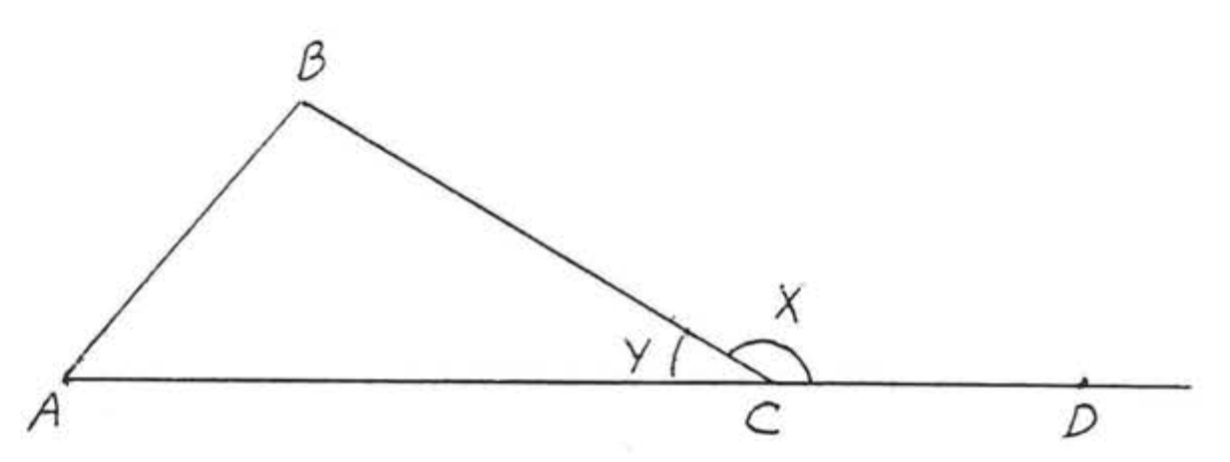
The results of Example 1.9.2.5 suggest the following theorem.
An exterior angle is equal to the sum of the two remote interior angles,
In Figure 1.9.2.3, ∠x=∠A+∠B.
Find x:
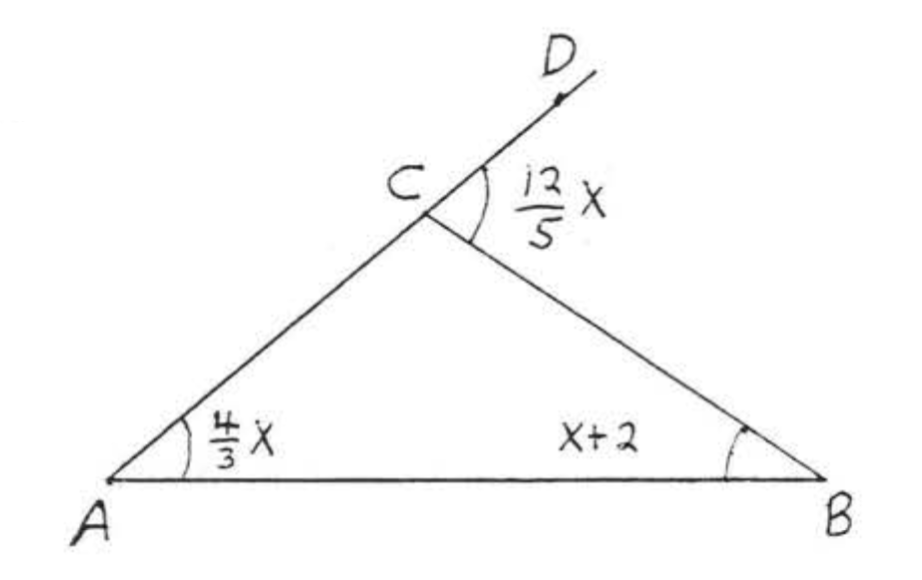
- Solution
-
∠BCD is an exterior angle with remote interior angles ∠A and ∠B. By Theorem 1.9.2.2,
∠BCD=∠A+∠B125x=43x+x+2
The least common denominator (1, c, d) is 15.
3(15)125x=3(15)43x+(15)x+(15)(2)36x=20x+15x+3036x=35x+3036x−35x=30x=30
Check:
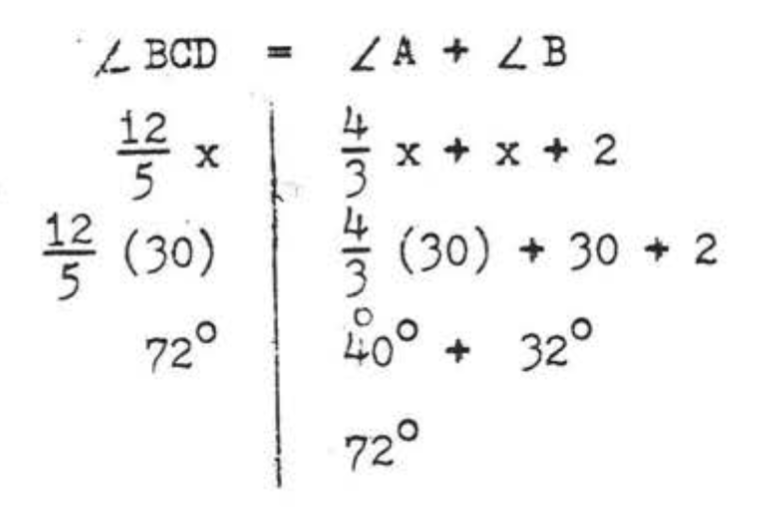
Answer: x=30.
Our work on the sum of the angles of a triangle can easily be extended to other figures:
Find the sum of the angles of a quadrilateral (four sided figure),
- Solution
-
Divide the quadrilateral into two triangles as illustrated,
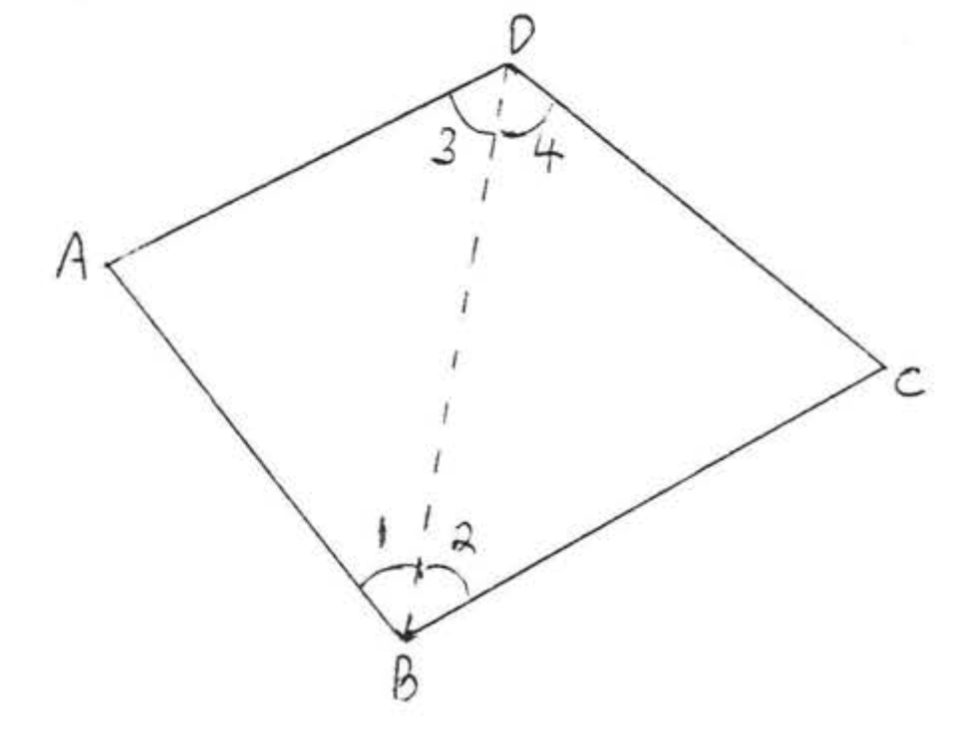
∠A+∠B+∠C+∠D=∠A+∠1+∠3+∠2+∠4+∠C=180∘+180∘=360∘
Answer: 360∘.
Find the sum of the angles of a pentagon (five-sided figure).
- Solution
-
Divide the pentagon into three triangles as illustrated, The sum is equal to the sum of the angles of the three triangle = (3)(180∘)=540∘.
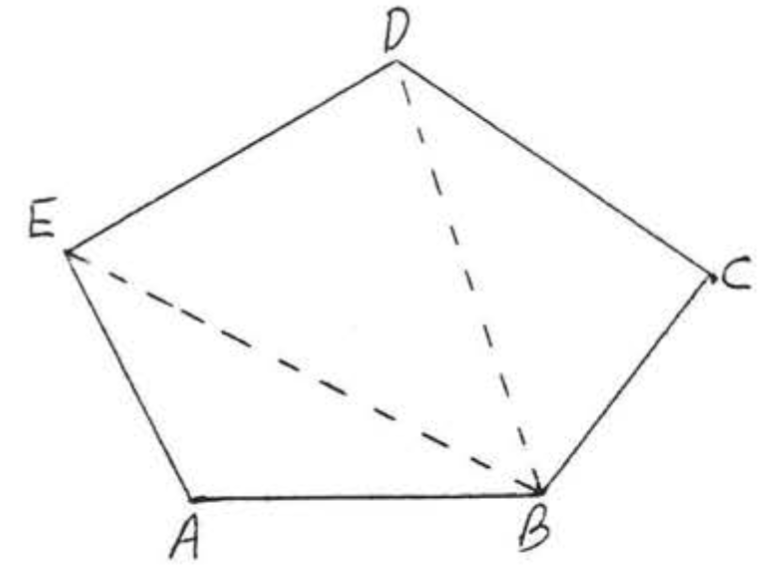
Answer: 540∘.
Identifying Congruent and Similar Triangles
Two triangles are congruent if they are exactly the same size and shape. In congruent triangles, the measures of corresponding angles and the lengths of corresponding sides are equal. Consider the two triangles shown below:
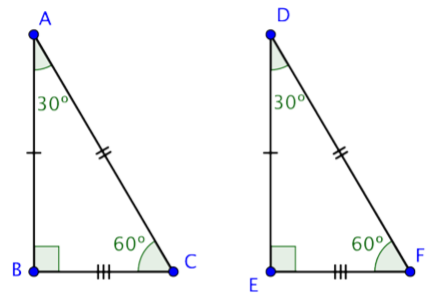
Since both ∠B and ∠E are right angles, these triangles are right triangles. Let’s call these two triangles ∆ABC and ∆DEF. These triangles are congruent if every pair of corresponding sides has equal lengths and every pair of corresponding angles has the same measure.
The corresponding sides are opposite the corresponding angles.
↔ means “corresponds to”
∠B ↔ ∠E
∠A ↔ ∠D
∠C ↔ ∠F
¯AB ↔ ¯DE
¯AC ↔ ¯DF
¯BC ↔ ¯EF
∆ABC and ∆DEF are congruent triangles as the corresponding sides and corresponding angles are equal.
Let’s take a look at another pair of triangles. Below are the triangles ∆ABC and ∆RST.
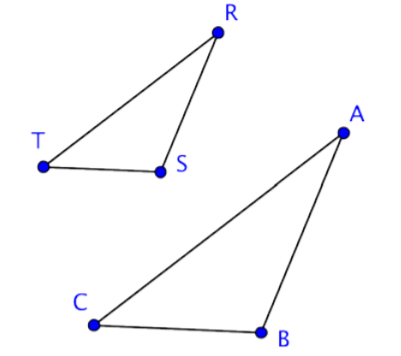
These two triangles are surely not congruent because ∆RST is clearly smaller in size than ∆ABC. But, even though they are not the same size, they do resemble one another. They are the same shape. The corresponding angles of these triangles look like they might have the same exact measurement, and if they did they would be congruent angles and we would call the triangles similar triangles.
Congruent angles are marked with hash marks, just as congruent sides are.
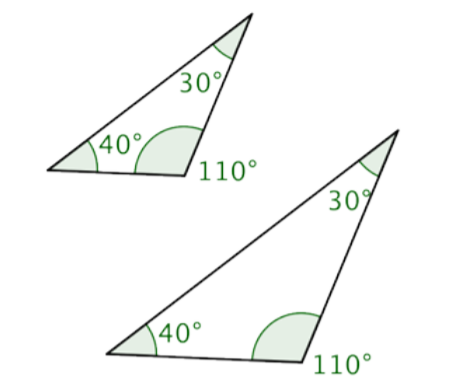
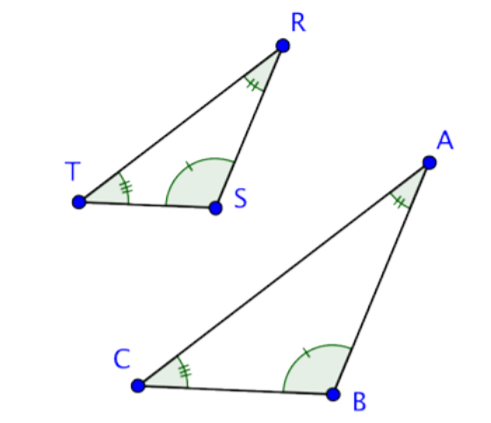
We can also show congruent angles by using multiple bands within the angle, rather than multiple hash marks on one band. Below is an image using multiple bands within the angle.
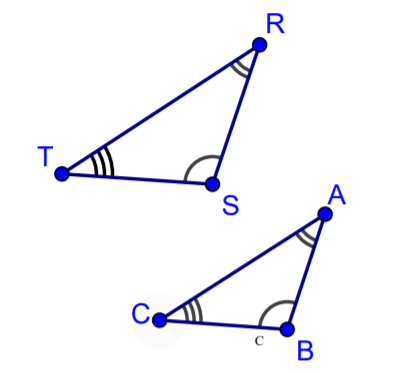
If the corresponding angles of two triangles have the same measurements they are called similar triangles. This name makes sense because they have the same shape, but not necessarily the same size. When a pair of triangles is similar, the corresponding sides are proportional to one another. That means that there is a consistent scale factor that can be used to compare the corresponding sides. In the previous example, the side lengths of the larger triangle are all 1.4 times the length of the smaller. So, similar triangles are proportional to one another.
Just because two triangles look similar does not mean they are similar triangles in the mathematical sense of the word. Checking that the corresponding angles have equal measure is one way of being sure the triangles are similar.
Corresponding Sides of Similar Triangles
There is another method for determining similarity of triangles that involves comparing the ratios of the lengths of the corresponding sides.
If the ratios of the pairs of corresponding sides are equal, the triangles are similar.
Consider the two triangles below.
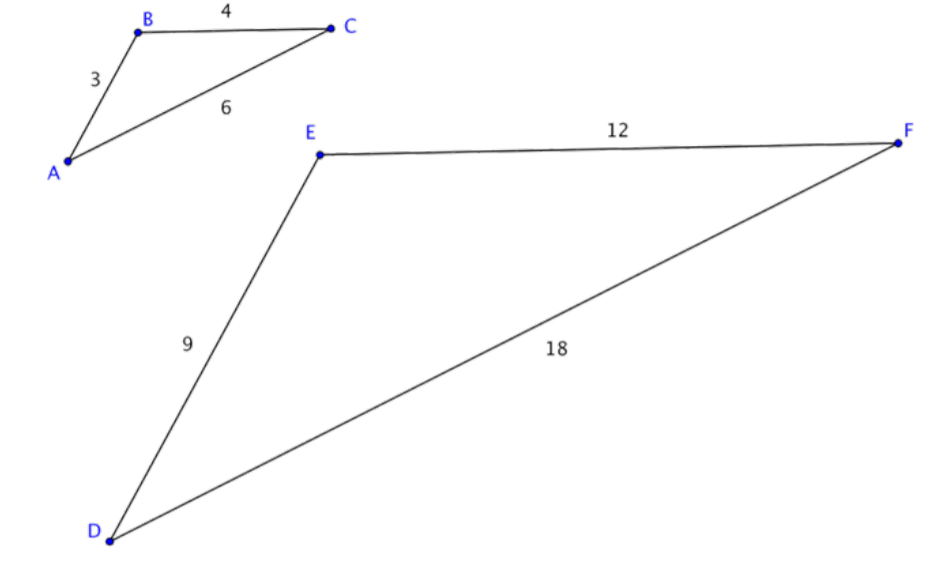
∆ABC is not congruent to ∆DEF because the side lengths of ∆DEF are longer than those of ∆ABC. So, are these triangles similar? If they are, the corresponding sides should be proportional.
Since these triangles are oriented in the same way, you can pair the left, right, and bottom sides: ¯AB and ¯DE, ¯BC and ¯EF, ¯AC and ¯DF. (You might call these the two shortest sides, the two longest sides, and the two leftover sides and arrive at the same ratios). Now we will look at the ratios of their lengths.
¯AB¯DE=¯BC¯EF=¯AC¯DF
Substituting the side length values into the proportion, you see that it is true:
39=412=618
If the corresponding sides are proportional, then the triangles are similar. Triangles ABC and DEF are similar, but not congruent.
Let’s use this idea of proportional corresponding sides to determine whether two more triangles are similar.
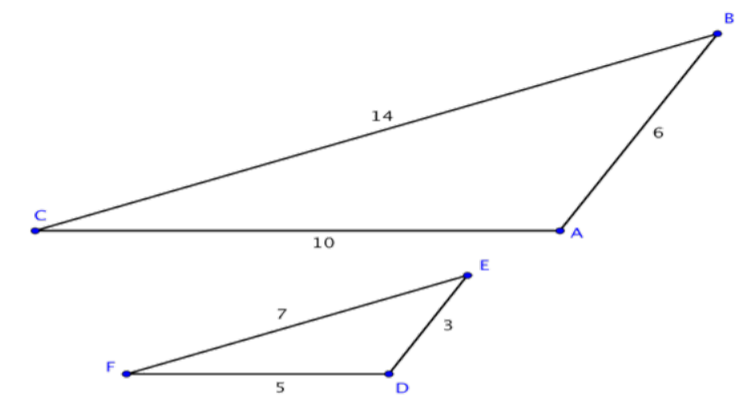
Determine if the triangles below are similar by seeing if their corresponding sides are proportional.
- Solution
-
First determine the corresponding sides, which are opposite corresponding angles.
¯CA ↔ ¯FD
¯AB ↔ ¯DE
¯BC ↔ ¯EF
Write the corresponding side lengths as ratios.
¯CA¯FD=¯AB¯DE=¯BC¯EF
Substitute the side lengths into the ratios, and determine if the ratios of the corresponding sides are equivalent. They are, so the triangles are similar.
105=63=147
2=2=2
Answer: ∆ABC and ∆DEF are similar.
The mathematical symbol ~ means “is similar to”. So, you can write ∆ABC is similar to ∆DEF as ∆ABC ~ ∆DEF.
Finding Missing Measurements in Similar Triangles
You can find the missing measurements in a triangle if you know some measurements of a similar triangle. Let’s look at an example.
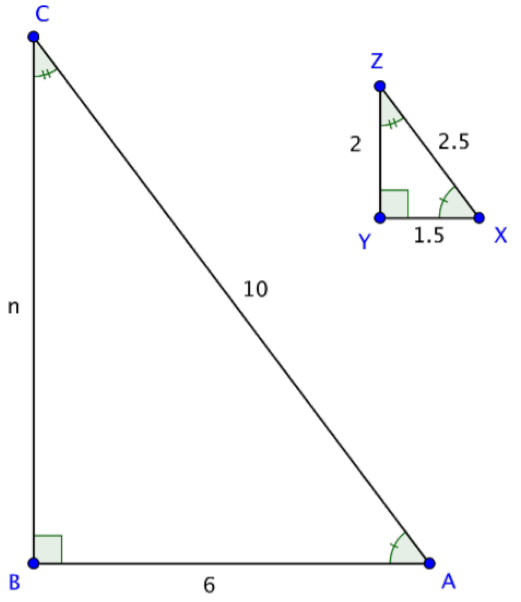
∆ABC and ∆XYZ are similar triangles. What is the length of side BC?
- Solution
-
In similar triangles, the ratios of corresponding sides are proportional. Set up a proportion of two ratios, one that includes the missing side.
BCYZ=ABXY
Substitute in the known side lengths for the side names in the ratio. Let the unknown side length be n.
n2=61.5
Solve for n using cross multiplication.
2⋅6=1.5⋅n
12=1.5n
8=n
This process is fairly straightforward—but be careful that your ratios represent corresponding sides, recalling that corresponding sides are opposite corresponding angles.
Solving Application Problems Involving Similar Triangles
Applying knowledge of triangles, similarity, and congruence can be very useful for solving problems in real life. Just as you can solve for missing lengths of a triangle drawn on a page, you can use triangles to find unknown distances between locations or objects.
Let’s consider the example of two trees and their shadows. Suppose the sun is shining down on two trees, one that is 6 feet tall and the other whose height is unknown. By measuring the length of each shadow on the ground, you can use triangle similarity to find the unknown height of the second tree.
First, let’s figure out where the triangles are in this situation. The trees themselves create one pair of corresponding sides. The shadows cast on the ground are another pair of corresponding sides. The third side of these imaginary similar triangles runs from the top of each tree to the tip of its shadow on the ground. This is the hypotenuse of the triangle.
If you know that the trees and their shadows form similar triangles, you can set up a proportion to find the height of the tree.
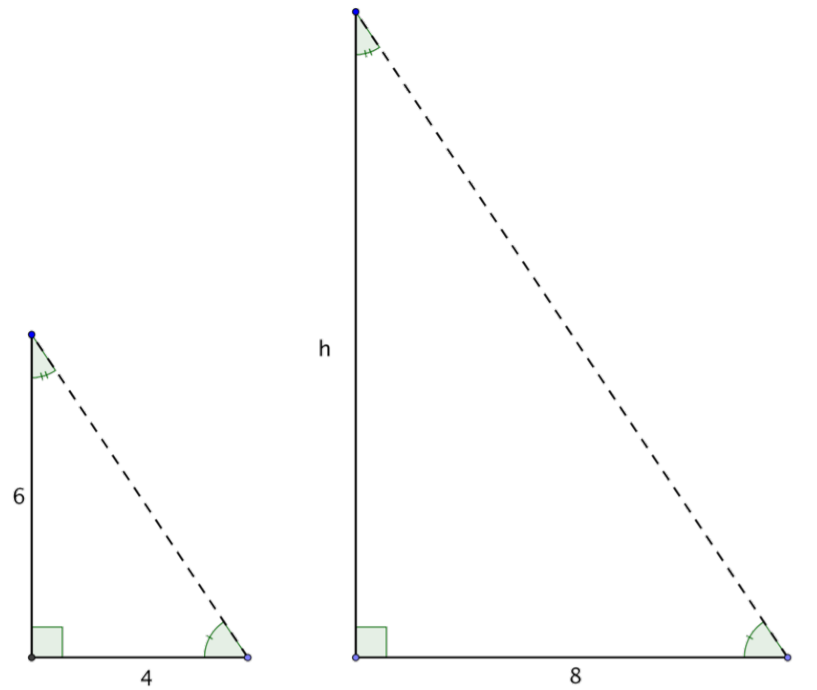
When the sun is at a certain angle in the sky, a 6-foot tree will cast a 4-foot shadow. How tall is a tree that casts an 8-foot shadow?
- Solution
-
The angle measurements are the same, so the triangles are similar triangles. Since they are similar triangles, you can use proportions to find the size of the missing side.
Tree 1Tree 2=Shadow 1Shadow 2
Set up a proportion comparing the heights of the trees and the lengths of their shadows.
Substitute in the known lengths. Call the missing tree height h.
6h=48
Solve for h using cross-multiplication.
6⋅8=4h
48=4h
12=h
Answer: The tree is 12 feet tall.
The Pythagorean Theorem
Pythagoras studied right triangles, and the relationships between the legs and the hypotenuse of a right triangle, before deriving his theory.
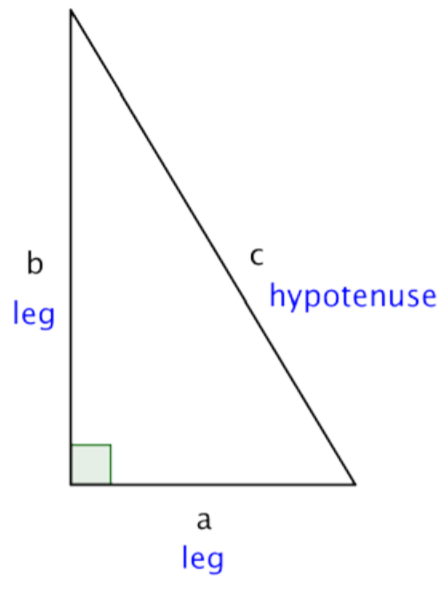
If a and b are the lengths of the legs of a right triangle and c is the length of the hypotenuse, then the sum of the squares of the lengths of the legs is equal to the square of the length of the hypotenuse.
This relationship is represented by the formula: a2+b2=c2
In the box above, you may have noticed the word “square,” as well as the small 2s to the top right of the letters in a2+b2=c2. To square a number means to multiply it by itself. So, for example, to square the number 5 you multiply 5⋅5, and to square the number 12, you multiply 12⋅12. Some common squares are shown in the table below.
| Number | Number Times Itself | Square |
| 1 | 12=1⋅1 | 1 |
| 2 | 22=2⋅2 | 4 |
| 3 | 32=3⋅3 | 9 |
| 4 | 42=4⋅4 | 16 |
| 5 | 52=5⋅5 | 25 |
| 10 | 102=10⋅10 | 100 |
When you see the equation a2+b2=c2, you can think of this as “the length of side a times itself, plus the length of side b times itself is the same as the length of side c times itself.”
Let’s try out all of the Pythagorean Theorem with an actual right triangle.
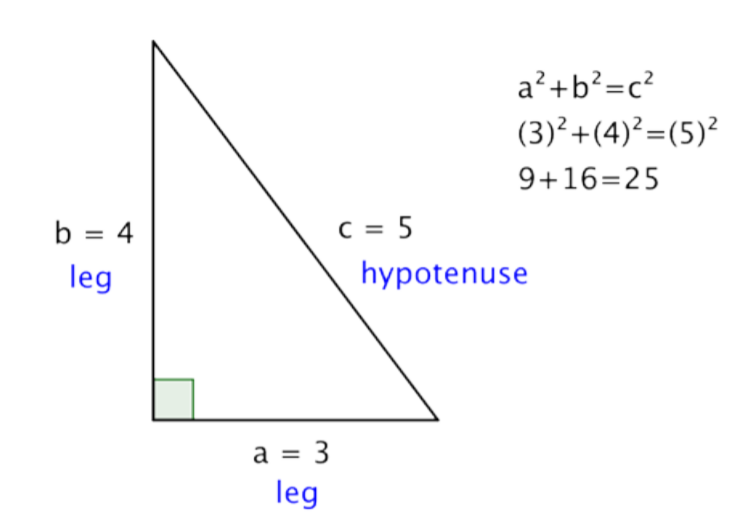
This theorem holds true for this right triangle—the sum of the squares of the lengths of both legs is the same as the square of the length of the hypotenuse. And, in fact, it holds true for all right triangles.
The Pythagorean Theorem can also be represented in terms of area. In any right triangle, the area of the square drawn from the hypotenuse is equal to the sum of the areas of the squares that are drawn from the two legs. You can see this illustrated below in the same 3-4-5 right triangle.
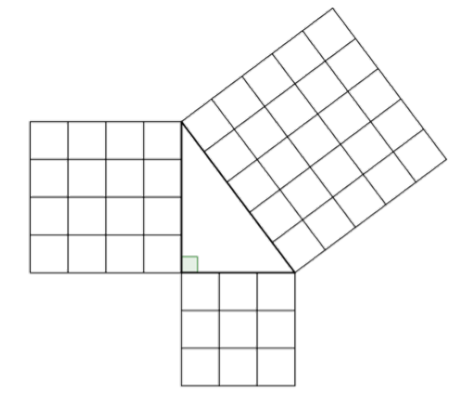
Note that the Pythagorean Theorem only works with right triangles.
Finding the Length of the Hypotenuse
You can use the Pythagorean Theorem to find the length of the hypotenuse of a right triangle if you know the length of the triangle’s other two sides, called the legs. Put another way, if you know the lengths of a and b, you can find c.
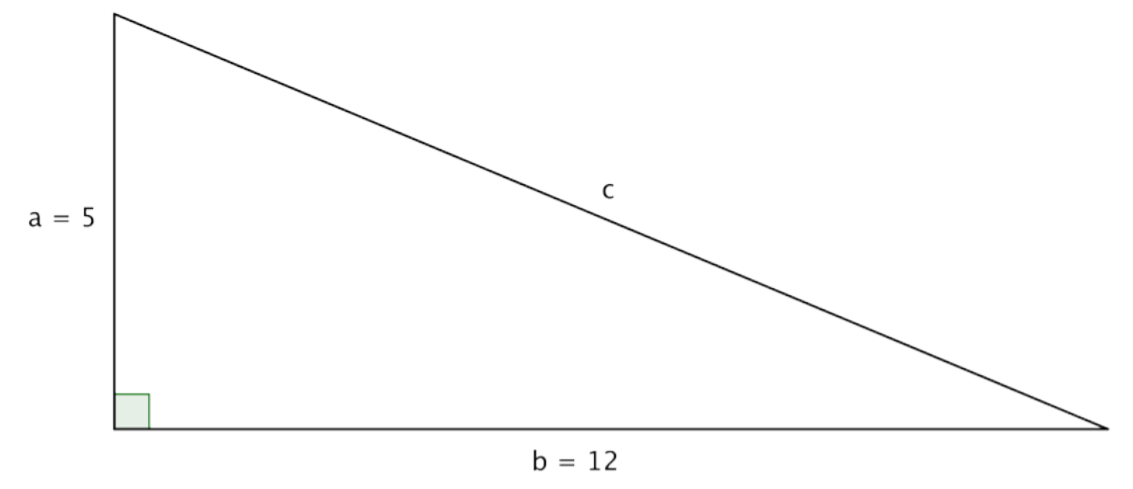
In the triangle above, you are given measures for legs a and b: 5 and 12, respectively. You can use the Pythagorean Theorem to find a value for the length of c, the hypotenuse.
The Pythagorean Theorem.
a2+b2=c2
Substitute known values for a and b.
(5)2+(12)2=c2
Evaluate.
25+144=c2
Simplify. To find the value of c, think about a number that, when multiplied by itself, equals 169. Does 10 work? How about 11? 12? 13? (You can use a calculator to multiply if the numbers are unfamiliar.)
169=c2
The square root of 169 is 13.
c=13
Using the formula, you find that the length of c, the hypotenuse, is 13.
Finding the Length of a Leg
You can use the same formula to find the length of a right triangle’s leg if you are given measurements for the lengths of the hypotenuse and the other leg. Consider the example below.
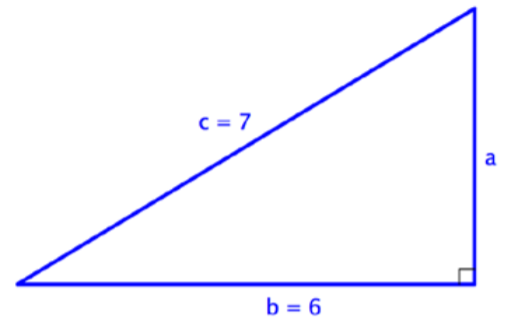
Find the length of side a in the triangle below. Use a calculator to estimate the square root to one decimal place.
- Solution
-
In this right triangle, you are given the measurements for the hypotenuse, c, and one leg, b. The hypotenuse is always opposite the right angle and it is always the longest side of the triangle.
a = ?
b = 6
c = 7
To find the length of leg a, substitute the known values into the Pythagorean Theorem.
a2+b2=c2
a2+62=72
Solve for a2. Think: what number, when added to 36, gives you 49?
a2+36=49
a2=13
Use a calculator to find the square root of 13. The calculator gives an answer of 3.6055…, which you can round to 3.6. (Since you are approximating, you use the symbol ≈.)
a≈3.6
Answer: a ≈ 3.6
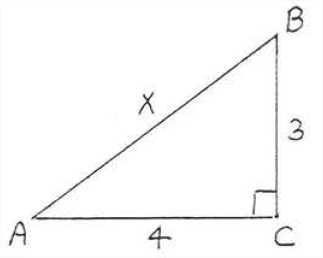
Find x
- Solution
-
leg2+leg2=hyp232+42=x29+16=x225=x25=x
Check:
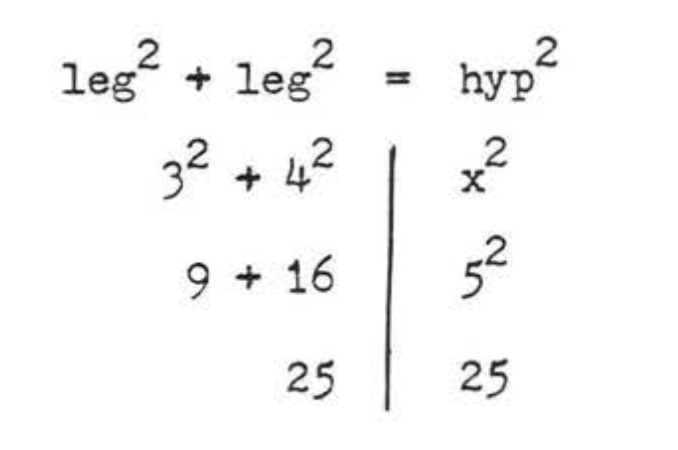
Answer: x=5.
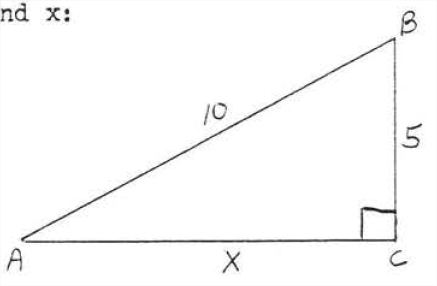
Find x:
- Solution
-
leg2+leg2=hyp252+x2=10225+x2=100x2=75x=√75=√25√3=5√3
Check:
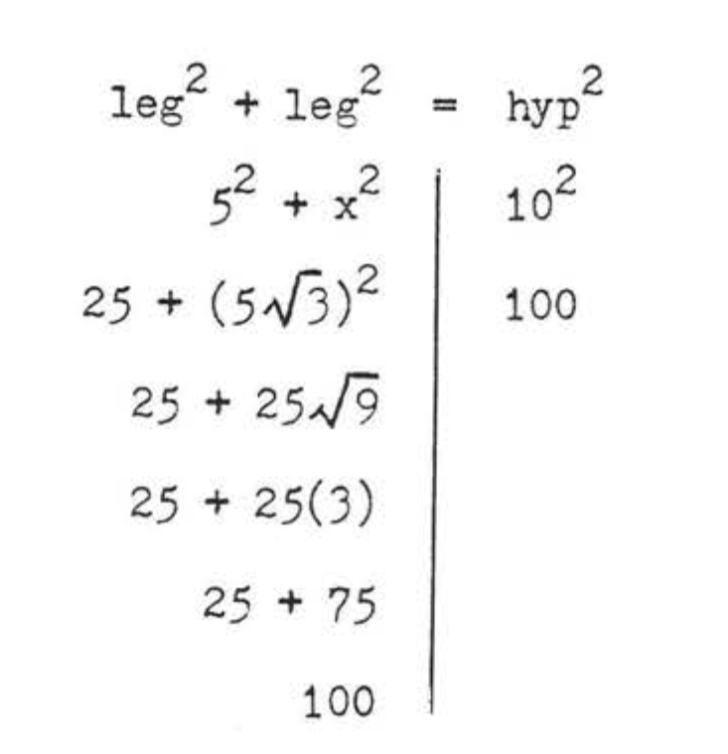
Answer: x=5√3.
Find x:
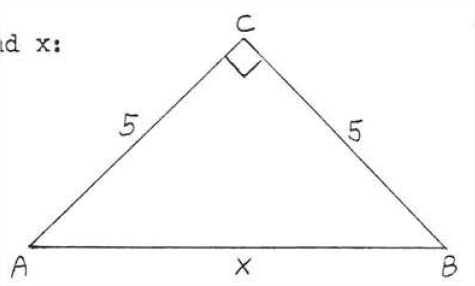
- Solution
-
leg2+leg2=hyp252+52=x225+25=x250=x2x=√50=√25√2=5√2
Check:
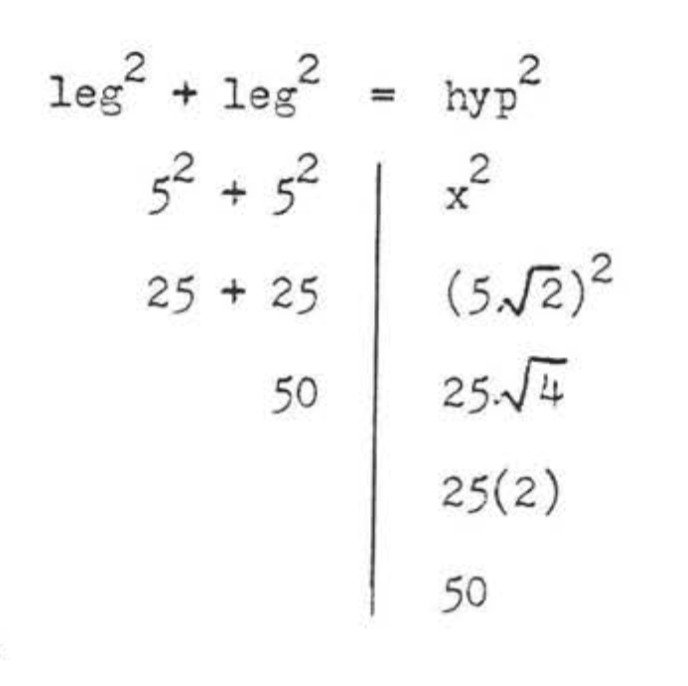
Answer: x=5√2.
Find x
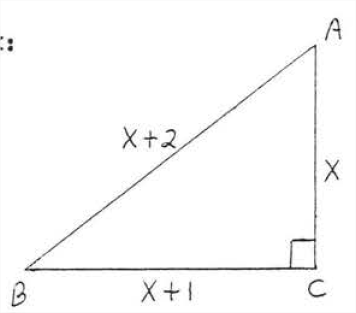
- Solution
-
leg2+leg2=hyp2x2+(x+1)2=(x+2)2x2+x2+2x+1=x2+4x+4x2+x2+2x+1−x2−4x−4=0x2−2x−3=0(x−3)(x+1)=0
x−3=0x=3 x+1=0x=−1
We reject x=−1 because AC=x cannot be negative.
Check, x=3:
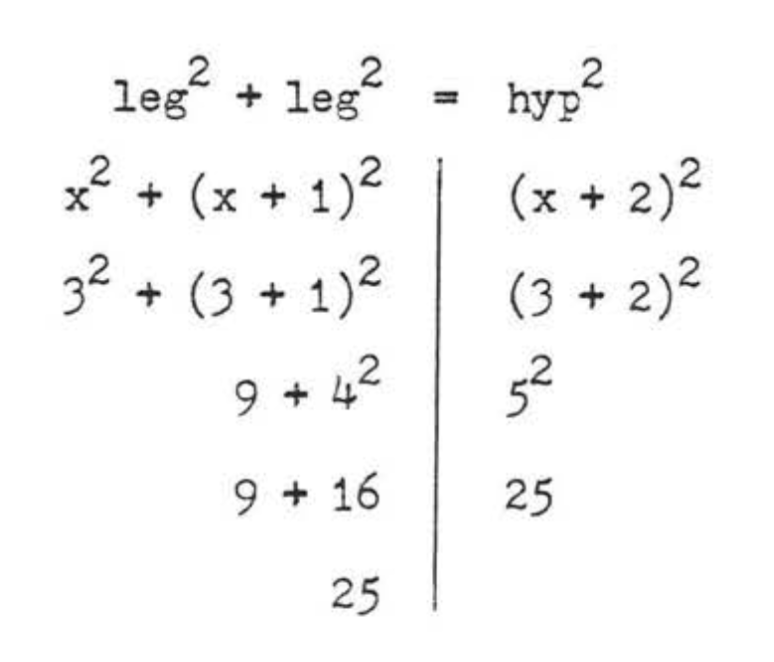
Answer: x=3.
Find x and AB:
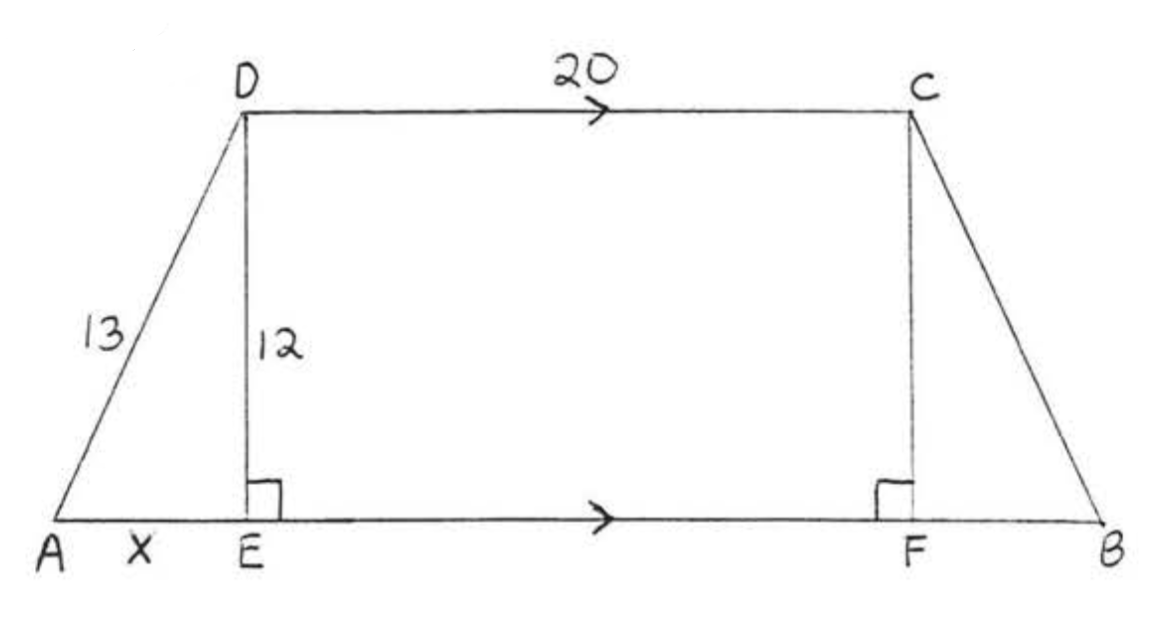
- Solution
-
x2+122=132x2+144=169x2=169−144x2=25x=5
CDEF is a rectangle so EF=CD=20 and CF=DE=12. Therefore FB=5 and AB=AE+EF+FB=5+20+5=30.
Answer: x=5, AB=30.
Find x, AC and BD:
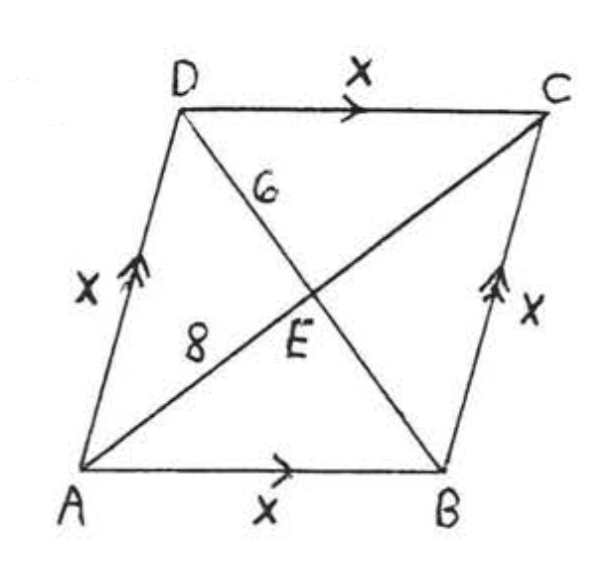
- Solution
-
ABCD is a rhombus. The diagonals of a rhombus are perpendicular and bisect each other.
62+82=x236+64=x2100=x210=x
AC=8+8=16,BD=6+6=12.
Answer: x=10,AC=16,BD=12.
Pythagoras (c. 582 - 507 B.C.) was not the first to discover the theorem which bears his name. It was known long before his time by the Chinese, the Babylonians, and perhaps also the Egyptians and the Hindus, According to tradition, Pythagoras was the first to give a nroof of the theorem, His proof probably made use of areas, like the one suggested. In Figure 1.9.2.5 below, (each square contains four congruent right triangles with sides of lengths a, b, and c, In addition the square on the left contains a square with side a and a square with side b while the one on the right contains a square with side c.)
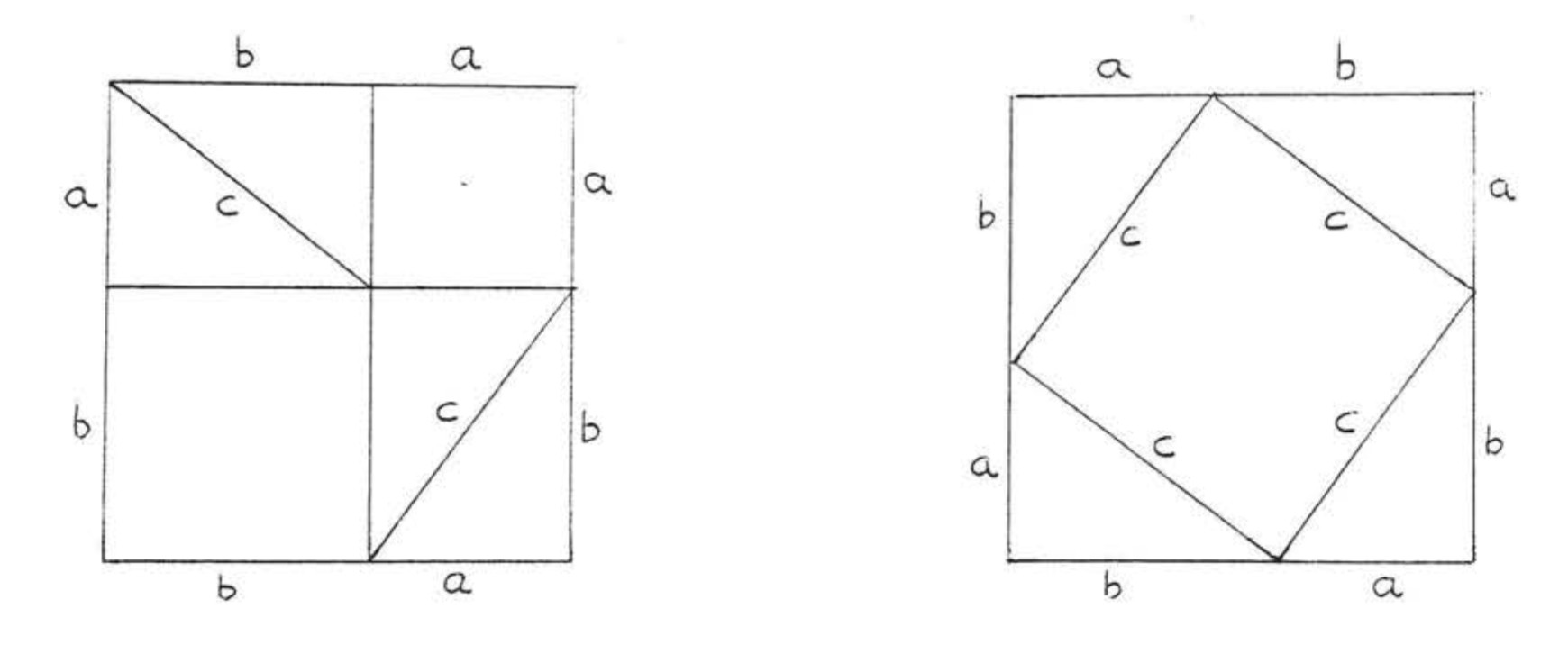
um theorem for triangles, the properties of parallel lines, and the theory of similar triangles and proportions.
Using the Pythagorean Theorem to Solve Real-world Problems
The Pythagorean Theorem is perhaps one of the most useful formulas you will learn in mathematics because there are so many applications of it in real world settings. Architects and engineers use this formula extensively when building ramps, bridges, and buildings. Look at the following examples.
The owners of a house want to convert a stairway leading from the ground to their back porch into a ramp. The porch is 3 feet off the ground, and due to building regulations, the ramp must start 12 feet away from the base of the porch. How long will the ramp be?
Use a calculator to find the square root, and round the answer to the nearest tenth.
- Solution
-
To solve a problem like this one, it often makes sense to draw a simple diagram showing where the legs and hypotenuse of the triangle lie.
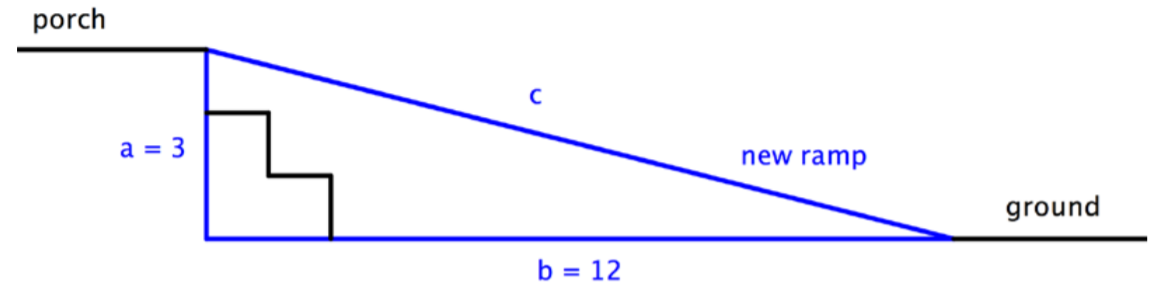
Identify the legs and the hypotenuse of the triangle. You know that the triangle is a right triangle since the ground and the raised portion of the porch are perpendicular—this means you can use the Pythagorean Theorem to solve this problem. Identify a, b, and c.
a = 3
b = 12
c = ?
Use the Pythagorean Theorem to find the length of c.
a2+b2=c2
32+122=c2
9+144=c2
153=c2
Use a calculator to find c.
12.4=c2
The square root of 153 is 12.369…, so you can round that to 12.4.
Answer: The ramp will be 12.4 feet long.
A sailboat has a large sail in the shape of a right triangle. The longest edge of the sail measures 17 yards, and the bottom edge of the sail is 8 yards. How tall is the sail?
- Solution
-
Draw an image to help you visualize the problem. In a right triangle, the hypotenuse will always be the longest side, so here it must be 17 yards. The problem also tells you that the bottom edge of the triangle is 8 yards.

Setup the Pythagorean Theorem.
a2+b2=c2
a2+82=172
a2+64=289
a2=225
15⋅15=225, so
a=15
Answer: The height of the sail is 15 yards.
The length of the shorter side of a right triangle is x and the length of the hypotenuse is r. Find the length of the longer side and find both of the angles, aside from the right angle, in the triangle.
- Answer
-
Draw the triangle such that it is obvious
which side is the shorter side →Pythagorean Theorem → r2=x2+y2
Subtract \x^2 from both sides of the equation → r2−x2=y2
Swap sides → y2=r2−x2
Take the square root of both
sides of the equation → \(y=\sqrt{r^2-x^2})\)By definition, the sine of θ is the side
opposite θ divided by the hypotenuse → sinθ=xr
Take the arcsine of both sides of the
equation in order to get θ by itself → θ=sin-1xrBy definition, the cosine of ϕ is the side
adjacent to ϕ divided by the hypotenuse → cosϕ= xrTake the arccosine of both sides of the
equation in order to get ϕ by itself → ϕ=cos1xrTo solve a problem like the one above, you need to memorize the relations between the sides and the angles of a right triangle. A convenient mnemonic2 for doing so is “SOHCAHTOA ”
pronounced as a single word.Referring to the diagram above right:
SOH reminds us that:: sinθ=OppositeHypotenuseCAH reminds us that:: cosθ=AdjacentHypotenuse
TOA reminds us that:: tanθ=OppositeAdhacentPoints to remember:
1. The angle θ is never the 90 degree angle.
2. The words “opposite” and “adjacent” designate sides relative to the angle. For instance,
the cosine of θ is the length of the side adjacent to θ divided by the length of the
hypotenuse.You also need to know about the arcsine and the arccosine functions to solve the example problem above. The arcsine function is the inverse of the sine function. The answer to the question, “What is the arcsine of 0.44?” is, “that angle whose sine is 0.44 .” There is an arcsine button on your calculator. It is typically labeled sin-1, to be read, “arcsine.” To use it you probably have to hit the inverse button or the second function button on your calculator first.
The inverse function of a function undoes what the function does. Thus:
sin-1sinθ =θ
Furthermore, the sine function is the inverse function to the arcsine function and the cosine function is the inverse function to the arccosine function. For the former, this means that:
sin(sin-1x)=x


