2.7.9: Solving a System of Linear Equations Using The Substitution Method
- Page ID
- 73611
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Solve a system of equations using the substitution method.
- Recognize systems of equations that have no solution or an infinite number of solutions.
- Solve application problems using the substitution method.
Using Substitution to Solve a System of Equations
In the substitution method, you solve for one variable and then substitute that expression into the other equation. The important thing here is that you are always substituting values that are equivalent.
For example:
Sean is 5 years older than four times his daughter’s age. His daughter is 7. How old is Sean?
You might do this problem in your head. Sean’s daughter is 7, so “four times his daughter’s age” is 28, and 5 years added to that is 33. Sean is 33.
If you solved the problem like that, you used a simple substitution—you substituted in the value “7” for “his daughter’s age.” You learned in the second part of the problem that “his daughter is 7.” So substituting in a value of “7” for “his daughter’s age” in the first part of the problem was okay, because you knew these two quantities were equal.
Let’s look at a simple system of equations that can be solved using substitution.
Find the value of \(\ x\) for this system.
Equation A: \(\ 4 x+3 y=-14\)
Equation B: \(\ y=2\)
- Solution
-
\(\ \begin{aligned}
4 x+3 y&=-14 \\
y&=2
\end{aligned}\)The problem asks to solve for \(\ x\).
Equation B gives you the value of \(\ y\), \(\ y=2\), so you can substitute 2 into Equation A for \(\ y\).
\(\ 4 x+3(2)=-14\) Substituting \(\ y=2\) into Equation A. \(\ \begin{aligned}
4 x+6&=-14 \\
4 x&=-20 \\
x&=-5
\end{aligned}\)Simplify and solve the equation for \(\ x\). \(\ x=-5\)
You can substitute a value for a variable even if it is an expression. Here’s an example.
Solve for \(\ x\) and \(\ y\).
Equation A: \(\ y+x=3\)
Equation B: \(\ x=y+5\)
- Solution
-
\(\ \begin{array}{l}
y+x=3 \\
x=y+5
\end{array}\)The goal of the substitution method is to rewrite one of the equations in terms of a single variable. Equation \(\ B\) tells us that \(\ x=y+5\), so it makes sense to substitute that \(\ y+5\) into Equation A for \(\ x\). \(\ \begin{array}{r}
y+{\color{blue}x}=3 \\
y+{\color{blue}(y+5)}=3
\end{array}\)Substitute \(\ y+5\) into Equation A for \(\ x\) and you get \(\ y+(y+5)=3\). \(\ \begin{array}{r}
2 y+5&= \ \ \ 3 \\
-5 & -5 \\
\hline 2 y\ \ \ \ \ \ & -2 \\
y\ \ \ \ \ \ &=-1
\end{array}\)Simplify and solve the equation to get \(\ y=-1\). \(\ \begin{array}{r}
y+x&=\ \ 3 \\
-1+x&= \ \ 3 \\
+1\ \ \ \ \ \ \ &+1 \\
\hline x&=\ \ 4
\end{array}\)To now find \(\ x\), substitute this value for \(\ y\) into either equation and solve for \(\ x\). We will use Equation A here to get \(\ x=4\). \(\ \begin{array}{r}
y+x=3 \\
-1+4=3 \\
3=3
\end{array}\)\(\ \begin{array}{r}
x=y+5 \\
4=-1+5 \\
4=4
\end{array}\)TRUE TRUE Finally, check the solution \(\ x=4\), \(\ y=-1\) by substituting these values into each of the original equations. \(\ x=4\) and \(\ y=-1\) The solution is \(\ (4,-1)\).
Remember, a solution to a system of equations must be a solution to each of the equations within the system. The ordered pair \(\ (4,-1)\) works for both equations, so you know that it is a solution to the system as well.
Let’s look at another example whose substitution involves the distributive property.
Solve for \(\ x\) and \(\ y\).
\(\ \begin{array}{c}
y=3 x+6 \\
-2 x+4 y=4
\end{array}\)
- Solution
-
\(\ \begin{array}{r}
y=3 x+6 \\
-2 x+4 y=4
\end{array}\)Choose an equation to use for the substitution.
The first equation tells you how to express \(\ y\) in terms of \(\ x\), so it makes sense to substitute \(\ 3 x+6\) into the second equation for \(\ y\).
\(\ \begin{array}{r}
-2 x+4 {\color{blue}y}=4 \\
-2 x+4{\color{blue}(3 x+6)}=4
\end{array}\)Substitute \(\ 3 x+6\) for \(\ y\) into the second equation. \(\ \begin{array}{r}
-2 x+12 x+24= & 4 \\
10 x+24= & 4 \\
\ -24\ \ \ \ & -24 \\
\hline 10 x\ \ \ \ \ \ \ \ \ = & -20 \\
x\ \ \ \ \ \ \ \ \ = & -2
\end{array}\)Simplify and solve the equation for \(\ x\). \(\ \begin{array}{r}
y=3 x+6 \\
y=3(-2)+6 \\
y=-6+6 \\
y=0
\end{array}\)To find \(\ y\), substitute this value for \(\ x\) back into one of the original equations. \(\ \begin{array}{r}
y=3 x+6 \\
0=3(-2)+6 \\
0=-6+6 \\
0=0
\end{array}\)\(\ \begin{array}{r}
-2 x+4 y=4 \\
-2(-2)+4(0)=4 \\
4+0=4 \\
4=4
\end{array}\)TRUE TRUE Check the solution \(\ x=-2\), \(\ y=0\) by substituting them into each of the original equations. \(\ x=-2\) and \(\ y=0\).
The solution is \(\ (-2,0)\).
In the examples above, one of the equations was already given to us in terms of the variable \(\ x\) or \(\ y\). This allowed us to quickly substitute that value into the other equation and solve for one of the unknowns.
Sometimes you may have to rewrite one of the equations in terms of one of the variables first before you can substitute. Look at the example below.
Solve for \(\ x\) and \(\ y\).
\(\ \begin{array}{c}
2 x+3 y=22 \\
3 x+y=19
\end{array}\)
- Solution
-
\(\ \begin{array}{r}
2 x+3 y=22 \\
3 x+y=19
\end{array}\)Choose an equation to use for the substitution. The second equation, \(\ 3 x+y=19\), can easily be rewritten in terms of \(\ y\), so it makes sense to start there. \(\ \begin{array}{l}
3 x+y=19 \\
y=19-3 x
\end{array}\)Rewrite \(\ 3 x+y=19\) in terms of \(\ y\). \(\ \begin{array}{r}
2 x+3 {\color{blue}y}=22 \\
2 x+3{\color{blue}(19-3 x)}=22
\end{array}\)Substitute \(\ 19-3 x\) for \(\ y\) in the other equation as \(\ 2 x+3(19-3 x)=22\). \(\ \begin{array}{r}
2 x+57-9 x=22 \\
-7 x+57=22 \\
-7 x=-35 \\
x=5
\end{array}\)Simplify and solve the equation for \(\ x\). \(\ \begin{array}{r}
3 x+y=19 \\
3(5)+y=19 \\
15+y=19 \\
y=19-15 \\
y=4
\end{array}\)Substitute \(\ x=5\) back into one of the original equations to solve for \(\ y\). \(\ \begin{aligned}
2 x+3 y &=22 \\
2(5)+3(4) &=22 \\
10+12 &=22 \\
22 &=22
\end{aligned}\)\(\ \begin{aligned}
3 x+y &=19 \\
3(5)+4 &=19 \\
19 &=19
\end{aligned}\)TRUE TRUE Check both solutions by substituting them into each of the original equations. \(\ x=5\) and \(\ y=4\)
The solution is \(\ (5,4)\).
Special Situations
There are some cases where using the substitution method will yield results that, at first, do not make sense. Let’s take a look at some of these and figure out what is going on.
Solve for \(\ x\) and \(\ y\).
\(\ \begin{array}{c}
y=5 x+4 \\
10 x-2 y=4
\end{array}\)
- Solution
-
\(\ \begin{array}{r}
y=5 x+4 \\
10 x-2 {\color{blue}y=4}
\end{array}\)\(\ 10 x-2\color{blue}(5 x+4)=4\)
Since the first equation is \(\ y=5 x+4\), you can substitute \(\ 5 x+4\) in for \(\ y\) in the second equation. \(\ 10 x-10 x-8=4\) Expand the expression on the left. \(\ \begin{aligned}
0-8 &=4 \\
-8 &=4
\end{aligned}\)Combine like terms on the left side of equation.
\(\ 10 x-10 x=0\), so you are left with \(\ -8=4\).
The statement \(\ -8=4\) is false, so there is no solution.
You get the false statement \(\ -8=4\). What does this mean? The graph of this system sheds some light on what is happening.
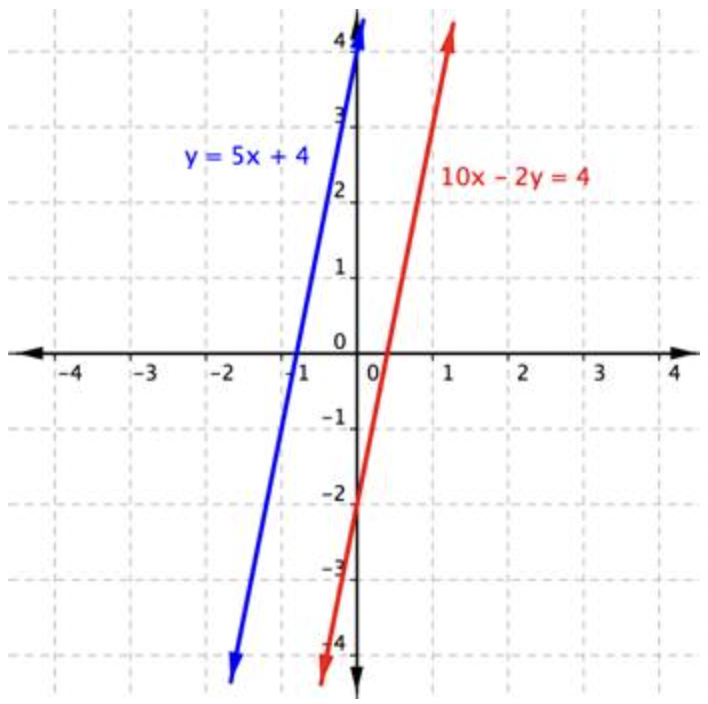
The lines are parallel. They never intersect and there is no solution to this system of linear equations. Note that the result \(\ -8=4\) is not a solution. It is simply a false statement and it indicates that there is no solution.
Now take this problem, which is interesting as well.
\(\ \begin{array}{c}
\color{green}\text { Solve for } x \text { and } y.\\
\color{green}y=-0.5x\\
\color{green}9y=-4.5x
\end{array}\)
Substituting \(\ -0.5 x\) for \(\ y\) in the second equation, you find the following:
\(\ \begin{aligned}
9 y &=-4.5 x \\
9(-0.5 x) &=-4.5 x \\
-4.5 x &=-4.5 x
\end{aligned}\)
This time, you get a true statement: \(\ -4.5 x=-4.5 x\). But what does this type of answer mean? Again, graphing can help you make sense of this system.
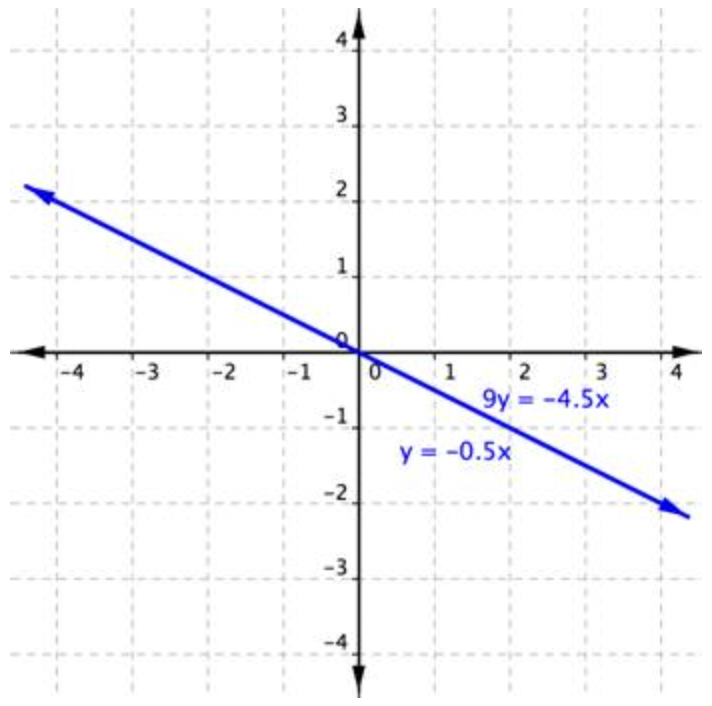
This system consists of two equations that both represent the same line; the two lines are collinear. Every point along the line will be a solution to the system, and that’s why the substitution method yields a true statement. In this case, there are an infinite number of solutions.
Solving Application Problems Using Substitution
Systems of equations are a very useful tool for modeling real-life situations and answering questions about them. If you can translate the application into two linear equations with two variables, then you have a system of equations that you can solve to find the solution. You can use any method to solve the system of equations. Use the substitution method in this topic.
In order to sell more of its produce, a local farm sells bags of apples in two sizes: medium and large. A medium bag contains 4 Macintosh and 1 Granny Smith apples and costs $2.80. A large bag contains 8 Macintosh and 4 Granny Smith apples and costs $7.20. The price of one Granny Smith apple is the same in the medium bag as it is in the large bag. The price of one Macintosh apple is the same in the medium bag as it is in the large bag. What is the price of each kind of apple?
Let’s start by creating a system of equations that represents what is happening in the problem. There are two types of apples and two sizes of bags. You can let \(\ m\) represent the cost of a Macintosh apple and \(\ g\) represent the cost of a Granny Smith apple. Let’s make a table and see what is known.
| Cost of Macintosh apples | + | Cost of Granny Smith apples | = | Total cost of bag | |
| Medium | \(\ 4m\) | + | \(\ g\) | = | $2.80 |
| Large | \(\ 8m\) | + | \(\ 4g\) | = | $7.20 |
Now that you have two equations in the same variables, you can solve the system. You will use substitution. The steps are shown in the example below:
Solve for \(\ g\) and \(\ m\) using the substitution method.
\(\ \begin{array}{c}
4 m+g=2.80 \\
8 m+4 g=7.20
\end{array}\)
- Solution
-
\(\ \begin{array}{l}
4 m+g=2.80 \\
g=2.80-4 m
\end{array}\)First, rewrite one of the equations in terms of one of the variables. \(\ \begin{array}{r}
8 m+4 \color{blue}g=7.20 \\
8 m+4\color{blue}(2.80-4 m)=7.20 \\
8 m+11.20-16 m=7.20 \\
8 m-16 m=7.20-11.20 \\
-8 m=-4.00 \\
m=0.50
\end{array}\)Substitute \(\ (2.80-4 m)\) for \(\ g\) in the second equation and solve for \(\ m\). \(\ \begin{array}{r}
4 m+g=2.80 \\
4(0.5)+g=2.80 \\
2+g=2.80 \\
g=2.80-2 \\
g=0.80
\end{array}\)Substitute the value of \(\ m\), \(\ 0.50\), into one of the original equations to solve for \(\ g\). \(\ \begin{aligned}
4 m+g &=2.80 \\
4(.50)+.80 &=2.80 \\
2.80 &=2.80
\end{aligned}\)Check both equations by substituting in the values of \(\ g\) and \(\ m\). \(\ \begin{aligned}
8 m+4 g &=7.20 \\
8(.50)+4(.80) &=7.20 \\
4.00+3.20 &=7.20 \\
7.20 &=7.20
\end{aligned}\)One Granny Smith apple costs $0.80 and one Macintosh apple costs $0.50.
Using the substitution method can be an effective approach to solving geometric problems.
The perimeter of a rectangle is 60 inches. If the length is 10 inches longer than the width, find the dimensions using the substitution method.
- Solution
-
\(\ \begin{array}{r}
2 l+2 w=60 \\
l=w+10
\end{array}\)Use the information provided to write a system of equations. Let \(\ l=\text { length }\) and \(\ w=\text { width }\). \(\ \begin{array}{r}
2 {\color{blue}l}\ \ \ \ \ \ \ \ \ \ \ \ \ +2 w&= \ \ \ 60 \\
2{\color{blue}(w+10)}+2 w & =\ \ \ 60 \\
2 w\ \ \ +20\ \ \ \ \ +2 w & =\ \ \ 60 \\
4 w\ \ \ \ \ +20&= \ \ \ 60 \\
-20 & -20 \\
\hline 4 w&=\ \ \ 40 \\
w&= \ \ \ 10
\end{array}\)Substitute \(\ w+10\) for \(\ l\) in the first equation and solve for \(\ w\). \(\ \begin{array}{r}
l=w+10 \\
l=10+10 \\
l=20
\end{array}\)To find \(\ l\), substitute 10 for \(\ w\) in one of the equations and solve for \(\ l\). \(\ \begin{array}{r}
l=w+10 \\
20=10+10 \\
20=20
\end{array}\)Check both solutions by substituting them into the two equations. \(\ \begin{array}{r}
2 l+2 w=60 \\
2(20)+2(10)=60 \\
40+20=60 \\
60=60
\end{array}\)Both of them are true, so this is a correct solution. The length of the rectangle is 20 inches.
The width of the rectangle is 10 inches.