3.6: Free Fall

Learning Objectives

• Use the kinematic equations with the variables y and g to analyze free-fall motion.
• Describe how the values of the position, velocity, and acceleration change during a free fall.
• Solve for the position, velocity, and acceleration as functions of time when an object is in a free fall.
• Use one-dimensional motion in perpendicular directions to analyze projectile motion.
• Calculate the range, time of flight, and maximum height of a projectile that is launched and impacts a flat, horizontal surface.
• Find the time of flight and impact velocity of a projectile that lands at a different height from that of launch.
• Calculate the trajectory of a projectile.

An interesting application of Equation 3.3.2 through Equation 3.5.22 is called free fall, which describes the motion of an object falling in a gravitational field, such as near the surface of Earth or other celestial objects of planetary size. Let’s assume the body is falling in a straight line perpendicular to the surface, so its motion is one-dimensional. For example, we can estimate the depth of a vertical mine shaft by dropping a rock into it and listening for the rock to hit the bottom. But “falling,” in the context of free fall, does not necessarily imply the body is moving from a greater height to a lesser height. If a ball is thrown upward, the equations of free fall apply equally to its ascent as well as its descent.

Gravity

The most remarkable and unexpected fact about falling objects is that if air resistance and friction are negligible, then in a given location all objects fall toward the center of Earth with the same constant acceleration, independent of their mass. This experimentally determined fact is unexpected because we are so accustomed to the effects of air resistance and friction that we expect light objects to fall slower than heavy ones. Until Galileo Galilei (1564–1642) proved otherwise, people believed that a heavier object has a greater acceleration in a free fall. We now know this is not the case. In the absence of air resistance, heavy objects arrive at the ground at the same time as lighter objects when dropped from the same height Figure \(\PageIndex{1}\).

Figure \(\PageIndex{1}\): A hammer and a feather fall with the same constant acceleration if air resistance is negligible. This is a general characteristic of gravity not unique to Earth, as astronaut David R. Scott demonstrated in 1971 on the Moon, where the acceleration from gravity is only 1.67 m/s² and there is no atmosphere.

In the real world, air resistance can cause a lighter object to fall slower than a heavier object of the same size. A tennis ball reaches the ground after a baseball dropped at the same time. (It might be difficult to observe the difference if the height is not large.) Air resistance opposes the motion of an object through the air, and friction between objects—such as between clothes and a laundry chute or between a stone and a pool into which it is dropped—also opposes motion between them.

For the ideal situations of these first few chapters, an object falling without air resistance or friction is defined to be in free fall. The force of gravity causes objects to fall toward the center of Earth. The acceleration of free-falling objects is therefore called acceleration due to gravity. Acceleration due to gravity is constant, which means we can apply the kinematic equations to any falling object where air resistance and friction are negligible. This opens to us a broad class of interesting situations.

Acceleration due to gravity is so important that its magnitude is given its own symbol, g. It is constant at any given location on Earth and has the average value

\[g = 9.81\; m/s^{2}\; (or\; 32.2\; ft/s^{2}) \ldotp\]

Although g varies from 9.78 m/s² to 9.83 m/s², depending on latitude, altitude, underlying geological formations, and local topography, let’s use an average value of 9.8 m/s² rounded to two significant figures in this text unless specified otherwise. Neglecting these effects on the value of g as a result of position on Earth’s surface, as well as effects resulting from Earth’s rotation, we take the direction of acceleration due to gravity to be downward (toward the center of Earth). In fact, its direction defines what we call vertical. Note that whether acceleration a in the kinematic equations has the value +g or -g depends on how we define our coordinate system. If we define the upward direction as positive, then a = -g = -9.8 m/s², and if we define the downward direction as positive, then a = g = 9.8 m/s².

One-Dimensional Motion Involving Gravity

The best way to see the basic features of motion involving gravity is to start with the simplest situations and then progress toward more complex ones. So, we start by considering straight up-and-down motion with no air resistance or friction. These assumptions mean the velocity (if there is any) is vertical. If an object is dropped, we know the initial velocity is zero when in free fall. When the object has left contact with whatever held or threw it, the object is in free fall. When the object is thrown, it has the same initial speed in free fall as it did before it was released. When the object comes in contact with the ground or any other object, it is no longer in free fall and its acceleration of g is no longer valid. Under these circumstances, the motion is one-dimensional and has constant acceleration of magnitude g. We represent vertical displacement with the symbol y.

Kinematic Equations for Objects in Free Fall

We assume here that acceleration equals -g (with the positive direction upward).

\[v =v _{0} - gt \label{3.15}\]

\[y = y_{0} + v_{0} t - \frac{1}{2} gt^{2} \label{3.16}\]

\[v^{2} = v_{0}^{2} - 2 g(y - y_{0}) \label{3.17}\]

Problem-Solving Strategy: Free Fall

1. Decide on the sign of the acceleration of gravity. In Equation \ref{3.15} through Equation \ref{3.17}, acceleration g is negative, which says the positive direction is upward and the negative direction is downward. In some problems, it may be useful to have acceleration g as positive, indicating the positive direction is downward.
2. Draw a sketch of the problem. This helps visualize the physics involved.
3. Record the knowns and unknowns from the problem description. This helps devise a strategy for selecting the appropriate equations to solve the problem.
4. Decide which of Equation \ref{3.15} through Equation \ref{3.17} are to be used to solve for the unknowns.

Example \(\PageIndex{1}\): Free Fall of a Ball

Figure \(\PageIndex{2}\) shows the positions of a ball, at 1-s intervals, with an initial velocity of 4.9 m/s downward, that is thrown from the top of a 98-m-high building. (a) How much time elapses before the ball reaches the ground? (b) What is the velocity when it arrives at the ground?

Figure \(\PageIndex{2}\): The positions and velocities at 1-s intervals of a ball thrown downward from a tall building at 4.9 m/s.

Strategy

Choose the origin at the top of the building with the positive direction upward and the negative direction downward. To find the time when the position is -98 m, we use Equation \ref{3.16}, with y₀ = 0, v₀ = -4.9 m/s, and g = 9.8 m/s².

Solution

1. Substitute the given values into the equation: \(y = y_{0} + v_{0} t - \frac{1}{2} gt^{2}\) \(-98.0\; m = 0 - (4.9\; m/s)t - \frac{1}{2} (9.8\; m/s^{2}) t^{2} \ldotp\) This simplifies to \(t^{2} + t - 20 = 0 \ldotp\) This is a quadratic equation with roots t = -5.0 s and t = 4.0 s. The positive root is the one we are interested in, since time t = 0 is the time when the ball is released at the top of the building. (The time t = -5.0 s represents the fact that a ball thrown upward from the ground would have been in the air for 5.0 s when it passed by the top of the building moving downward at 4.9 m/s.)
2. Using Equation \ref{3.15}, we have \(v =v _{0} - gt = -4.9\; m/s - (9.8\; m/s^{2})(4.0\; s) = -44.1\; m/s \ldotp\)

Significance

For situations when two roots are obtained from a quadratic equation in the time variable, we must look at the physical significance of both roots to determine which is correct. Since t = 0 corresponds to the time when the ball was released, the negative root would correspond to a time before the ball was released, which is not physically meaningful. When the ball hits the ground, its velocity is not immediately zero, but as soon as the ball interacts with the ground, its acceleration is not g and it accelerates with a different value over a short time to zero velocity. This problem shows how important it is to establish the correct coordinate system and to keep the signs of g in the kinematic equations consistent.

Example \(\PageIndex{2}\): Vertical Motion of a Baseball

A batter hits a baseball straight upward at home plate and the ball is caught 5.0 s after it is struck Figure \(\PageIndex{3}\). (a) What is the initial velocity of the ball? (b) What is the maximum height the ball reaches? (c) How long does it take to reach the maximum height? (d) What is the acceleration at the top of its path? (e) What is the velocity of the ball when it is caught? Assume the ball is hit and caught at the same location.

Figure \(\PageIndex{3}\): A baseball hit straight up is caught by the catcher 5.0 s later.

Strategy

Choose a coordinate system with a positive y-axis that is straight up and with an origin that is at the spot where the ball is hit and caught.

Solution

1. Equation \ref{3.16} gives \(y = y_{0} + v_{0} t - \frac{1}{2} gt^{2}\) \(0 = 0 + v_{0} (5.0\; s)- \frac{1}{2} (9.8\; m/s^{2}) (5.0\; s)^{2} \ldotp\) which gives v₀ = 24.5 m/sec.
2. At the maximum height, v = 0. With v₀ = 24.5 m/s, Equation \ref{3.17} gives \(v^{2} = v_{0}^{2} - 2 g(y - y_{0})\) \(0 = (24.5\; m/s^{2}) - 2 (9.8\; m/s^{2})(y - 0)\) or \(y = 30.6\; m \ldotp\)
3. To find the time when v = 0 , we use Equation \ref{3.15}: \(v = v_{0} - gt\) \(0 = 24..5\; m/s - (9.8\; m/s^{2})t \ldotp\) This gives t = 2.5 s. Since the ball rises for 2.5 s, the time to fall is 2.5 s.
4. The acceleration is 9.8 m/s² everywhere, even when the velocity is zero at the top of the path. Although the velocity is zero at the top, it is changing at the rate of 9.8 m/s² downward.
5. The velocity at t = 5.0 s can be determined with Equation \ref{3.15}: \(\begin{split} v & = v_{0} - gt \\ & = 24.5\; m/s - 9.8\; m/s^{2} (5.0\; s) \\ & = -24.5\; m/s \ldotp \end{split}\)

Significance

The ball returns with the speed it had when it left. This is a general property of free fall for any initial velocity. We used a single equation to go from throw to catch, and did not have to break the motion into two segments, upward and downward. We are used to thinking of the effect of gravity is to create free fall downward toward Earth. It is important to understand, as illustrated in this example, that objects moving upward away from Earth are also in a state of free fall.

Example \(\PageIndex{3}\): Rocket Booster

A small rocket with a booster blasts off and heads straight upward. When at a height of 5.0 km and velocity of 200.0 m/s, it releases its booster. (a) What is the maximum height the booster attains? (b) What is the velocity of the booster at a height of 6.0 km? Neglect air resistance.

Figure \(\PageIndex{4}\): A rocket releases its booster at a given height and velocity. How high and how fast does the booster go?

Strategy

We need to select the coordinate system for the acceleration of gravity, which we take as negative downward. We are given the initial velocity of the booster and its height. We consider the point of release as the origin. We know the velocity is zero at the maximum position within the acceleration interval; thus, the velocity of the booster is zero at its maximum height, so we can use this information as well. From these observations, we use Equation \ref{3.17}, which gives us the maximum height of the booster. We also use Equation \ref{3.17} to give the velocity at 6.0 km. The initial velocity of the booster is 200.0 m/s.

Solution

1. From Equation \ref{3.17}, \(v^{2} = v_{0}^{2} - 2 g(y - y_{0})\). With v = 0 and y₀ = 0, we can solve for y: \(y = \frac{v_{0}^{2}}{-2g} = \frac{(2.0 \times 10^{2}\; m/s)^{2}}{-2(9.8\; m/s^{2})} = 2040.8\; m \ldotp\) This solution gives the maximum height of the booster in our coordinate system, which has its origin at the point of release, so the maximum height of the booster is roughly 7.0 km.
2. An altitude of 6.0 km corresponds to y = 1.0 x 10³ m in the coordinate system we are using. The other initial conditions are y₀ = 0, and v₀ = 200.0 m/s. We have, from Equation \ref{3.17}, \(v^{2} = (200.0\; m/s)^{2} - 2(9.8\; m/s^{2})(1.0 \times 10^{3}\; m) \Rightarrow v = \pm 142.8\; m/s \ldotp\)

Significance

We have both a positive and negative solution in (b). Since our coordinate system has the positive direction upward, the +142.8 m/s corresponds to a positive upward velocity at 6000 m during the upward leg of the trajectory of the booster. The value v = -142.8 m/s corresponds to the velocity at 6000 m on the downward leg. This example is also important in that an object is given an initial velocity at the origin of our coordinate system, but the origin is at an altitude above the surface of Earth, which must be taken into account when forming the solution.

Two-Dimensional Motion Involving Gravity-Projectile Motion

Projectile motion is the motion of an object thrown or projected into the air, subject only to acceleration as a result of gravity. The applications of projectile motion in physics and engineering are numerous. Some examples include meteors as they enter Earth’s atmosphere, fireworks, and the motion of any ball in sports. Such objects are called projectiles and their path is called a trajectory. The motion of falling objects as discussed in Motion Along a Straight Line is a simple one-dimensional type of projectile motion in which there is no horizontal movement. In this section, we consider two-dimensional projectile motion, and our treatment neglects the effects of air resistance.

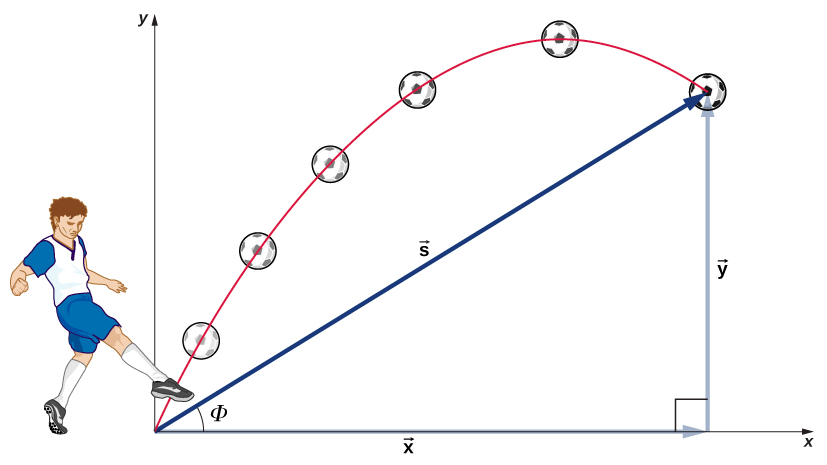
The most important fact to remember here is that motions along perpendicular axes are independent and thus can be analyzed separately. We discussed this fact in Displacement and Velocity Vectors, where we saw that vertical and horizontal motions are independent. The key to analyzing two-dimensional projectile motion is to break it into two motions: one along the horizontal axis and the other along the vertical. (This choice of axes is the most sensible because acceleration resulting from gravity is vertical; thus, there is no acceleration along the horizontal axis when air resistance is negligible.) As is customary, we call the horizontal axis the x-axis and the vertical axis the y-axis. It is not required that we use this choice of axes; it is simply convenient in the case of gravitational acceleration. In other cases we may choose a different set of axes. Figure \(\PageIndex{1}\) illustrates the notation for displacement, where we define \(\vec{s}\) to be the total displacement, and \(\vec{x}\) and \(\vec{y}\) are its component vectors along the horizontal and vertical axes, respectively. The magnitudes of these vectors are s, x, and y.

Figure \(\PageIndex{1}\): The total displacement s of a soccer ball at a point along its path. The vector \(\vec{s}\) has components \(\vec{x}\) and \(\vec{y}\) along the horizontal and vertical axes. Its magnitude is s and it makes an angle \(\phi\) with the horizontal.

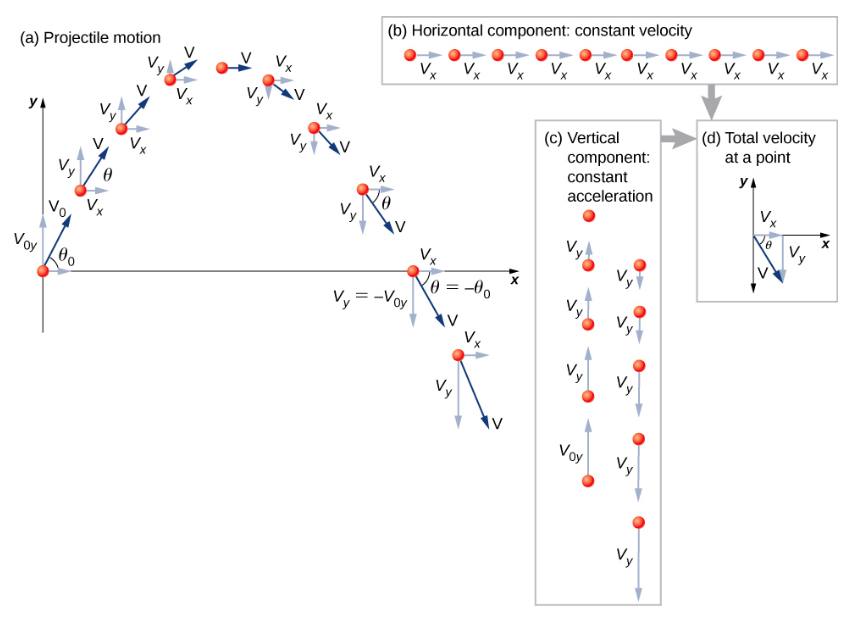
To describe projectile motion completely, we must include velocity and acceleration, as well as displacement. We must find their components along the x- and y-axes. Let’s assume all forces except gravity (such as air resistance and friction, for example) are negligible. Defining the positive direction to be upward, the components of acceleration are then very simple:

\[a_{y} = -g = -9.8\; m/s^{2} (- 32\; ft/s^{2}) \ldotp\]

Because gravity is vertical, a_x = 0. If a_x = 0, this means the initial velocity in the x direction is equal to the final velocity in the x direction, or v_x = v_0x. With these conditions on acceleration and velocity, we can write the kinematic Equation 4.11 through Equation 4.18 for motion in a uniform gravitational field, including the rest of the kinematic equations for a constant acceleration from Motion with Constant Acceleration. The kinematic equations for motion in a uniform gravitational field become kinematic equations with a_y = -g, a_x = 0:

Horizontal Motion

\[v_{0x} = v_{x}, \quad x = x_{0} + v_{x} t \label{4.19}\]

Vertical Motion

\[y = y_{0} + \frac{1}{2} (v_{0y} + v_{y})t \label{4.20}\]

\[v_{y} = v_{0y} - gt \label{4.21}\]

\[y = y_{0} + v_{0y} t - \frac{1}{2} g t^{2} \label{4.22}\]

\[v_{y}^{2}= v_{0y}^{2} + 2g(y - y_{0}) \label{4.23}\]

Using this set of equations, we can analyze projectile motion, keeping in mind some important points.

Problem-Solving Strategy: Projectile Motion

1. Resolve the motion into horizontal and vertical components along the x- and y-axes. The magnitudes of the components of displacement \(\vec{s}\) along these axes are x and y. The magnitudes of the components of velocity \(\vec{v}\) are v_x = vcos\(\theta\) and v_y = vsin\(\theta\), where v is the magnitude of the velocity and \(\theta\) is its direction relative to the horizontal, as shown in Figure \(\PageIndex{2}\).
2. Treat the motion as two independent one-dimensional motions: one horizontal and the other vertical. Use the kinematic equations for horizontal and vertical motion presented earlier.
3. Solve for the unknowns in the two separate motions: one horizontal and one vertical. Note that the only common variable between the motions is time t. The problem-solving procedures here are the same as those for one-dimensional kinematics and are illustrated in the following solved examples.
4. Recombine quantities in the horizontal and vertical directions to find the total displacement \(\vec{s}\) and velocity \(\vec{v}\). Solve for the magnitude and direction of the displacement and velocity using \(s = \sqrt{x^{2} + y^{2}} \ldotp \quad \phi = \tan^{-1} \left(\dfrac{y}{x}\right), \quad v = \sqrt{v_{x}^{2} + v_{y}^{2}} \ldotp\) where \(\phi\) is the direction of the displacement \(\vec{s}\).

Figure \(\PageIndex{2}\): (a) We analyze two-dimensional projectile motion by breaking it into two independent one-dimensional motions along the vertical and horizontal axes. (b) The horizontal motion is simple, because a_x = 0 and v_x is a constant. (c) The velocity in the vertical direction begins to decrease as the object rises. At its highest point, the vertical velocity is zero. As the object falls toward Earth again, the vertical velocity increases again in magnitude but points in the opposite direction to the initial vertical velocity. (d) The x and y motions are recombined to give the total velocity at any given point on the trajectory.

Example \(\PageIndex{4}\): A Fireworks Projectile Explodes high and away

During a fireworks display, a shell is shot into the air with an initial speed of 70.0 m/s at an angle of 75.0° above the horizontal, as illustrated in Figure \(\PageIndex{3}\). The fuse is timed to ignite the shell just as it reaches its highest point above the ground. (a) Calculate the height at which the shell explodes. (b) How much time passes between the launch of the shell and the explosion? (c) What is the horizontal displacement of the shell when it explodes? (d) What is the total displacement from the point of launch to the highest point?

Figure \(\PageIndex{3}\): The trajectory of a fireworks shell. The fuse is set to explode the shell at the highest point in its trajectory, which is found to be at a height of 233 m and 125 m away horizontally.

Strategy

The motion can be broken into horizontal and vertical motions in which a_x = 0 and a_y = -g. We can then define x₀ and y₀ to be zero and solve for the desired quantities.

Solution

1. By “height” we mean the altitude or vertical position y above the starting point. The highest point in any trajectory, called the apex, is reached when v_y = 0. Since we know the initial and final velocities, as well as the initial position, we use the following equation to find y: \(v_{y}^{2} = v_{0y}^{2} - 2g(y - y_{0}) \ldotp\) Because y₀ and v_y are both zero, the equation simplifies to \(0 = v_{0y}^{2} - 2gy \ldotp\) Solving for y gives \(y = \frac{v_{0y}^{2}}{2g} \ldotp\) Now we must find v_0y, the component of the initial velocity in the y direction. It is given by v_0y = v₀ sin\(\theta_{0}\), where v₀ is the initial velocity of 70.0 m/s and \(\theta_{0}\) = 75° is the initial angle. Thus \(v_{0y} = v_{0} \sin \theta = (70.0\; m/s) \sin 75^{o} = 67.6\; m/s\) and y is \(y = \frac{(67.6\; m/s)^{2}}{2(9.80\; m/s^{2})} \ldotp\) Thus, we have \(y = 233\; m \ldotp\) Note that because up is positive, the initial vertical velocity is positive, as is the maximum height, but the acceleration resulting from gravity is negative. Note also that the maximum height depends only on the vertical component of the initial velocity, so that any projectile with a 67.6-m/s initial vertical component of velocity reaches a maximum height of 233 m (neglecting air resistance). The numbers in this example are reasonable for large fireworks displays, the shells of which do reach such heights before exploding. In practice, air resistance is not completely negligible, so the initial velocity would have to be somewhat larger than that given to reach the same height.
2. As in many physics problems, there is more than one way to solve for the time the projectile reaches its highest point. In this case, the easiest method is to use v_y = v_0y - gt. Because v_y = 0 at the apex, this equation reduces \(0 = v_{0y} - gt\) or \(t = \frac{v_{0y}}{g} = \frac{67.6\; m/s}{9.80\; m/s^{2}} = 6.90\; s \ldotp\) This time is also reasonable for large fireworks. If you are able to see the launch of fireworks, notice that several seconds pass before the shell explodes. Another way of finding the time is by using y = y₀ + \(\frac{1}{2}\)(v_0y + v_y)t. This is left for you as an exercise to complete.
3. Because air resistance is negligible, a_x = 0 and the horizontal velocity is constant, as discussed earlier. The horizontal displacement is the horizontal velocity multiplied by time as given by x = x₀ + v_xt, where x₀ is equal to zero. Thus, \(x = v_{x} t,\) where v_x is the x-component of the velocity, which is given by \(v_{x} = v_{0} \cos \theta = (70.0\; m/s) \cos 75^{o} = 18.1\; m/s \ldotp\) Time t for both motions is the same, so x is \(x = (18.1\; m/s)(6.90\; s) = 125\; m \ldotp\) Horizontal motion is a constant velocity in the absence of air resistance. The horizontal displacement found here could be useful in keeping the fireworks fragments from falling on spectators. When the shell explodes, air resistance has a major effect, and many fragments land directly below.
4. The horizontal and vertical components of the displacement were just calculated, so all that is needed here is to find the magnitude and direction of the displacement at the highest point: \(\vec{s} = 125 \hat{i} + 233 \hat{j}\) \(|\vec{s}| = \sqrt{125^{2} + 233^{2}} = 264\; m\) \(\theta = \tan^{-1} \left(\dfrac{233}{125}\right) = 61.8^{o} \ldotp\) Note that the angle for the displacement vector is less than the initial angle of launch. To see why this is, review Figure \(\PageIndex{1}\), which shows the curvature of the trajectory toward the ground level. When solving Example 4.7(a), the expression we found for y is valid for any projectile motion when air resistance is negligible. Call the maximum height y = h. Then, \(h = \frac{v_{0y}^{2}}{2g} \ldotp\) This equation defines the maximum height of a projectile above its launch position and it depends only on the vertical component of the initial velocity.

Example \(\PageIndex{5}\): Calculating projectile motion- Tennis Player

A tennis player wins a match at Arthur Ashe stadium and hits a ball into the stands at 30 m/s and at an angle 45° above the horizontal (Figure \(\PageIndex{4}\)). On its way down, the ball is caught by a spectator 10 m above the point where the ball was hit. (a) Calculate the time it takes the tennis ball to reach the spectator. (b) What are the magnitude and direction of the ball’s velocity at impact?

Figure \(\PageIndex{4}\): The trajectory of a tennis ball hit into the stands.

Strategy

Again, resolving this two-dimensional motion into two independent one-dimensional motions allows us to solve for the desired quantities. The time a projectile is in the air is governed by its vertical motion alone. Thus, we solve for t first. While the ball is rising and falling vertically, the horizontal motion continues at a constant velocity. This example asks for the final velocity. Thus, we recombine the vertical and horizontal results to obtain \(\vec{v}\) at final time t, determined in the first part of the example.

Solution

1. While the ball is in the air, it rises and then falls to a final position 10.0 m higher than its starting altitude. We can find the time for this by using Equation \ref{4.22}: \(y = y_{0} + v_{0y}t - \frac{1}{2} gt^{2} \ldotp\) If we take the initial position y₀ to be zero, then the final position is y = 10 m. The initial vertical velocity is the vertical component of the initial velocity: \(v_{0y} = v_{0} \sin \theta_{0} = (30.0\; m/s) \sin 45^{o} = 21.2\; m/s \ldotp\) Substituting into Equation \ref{4.22} for y gives us \(10.0\; m = (21.2\; m/s)t - (4.90\; m/s^{2})t^{2} \ldotp\) Rearranging terms gives a quadratic equation in t: \((4.90\; m/s^{2})t^{2} - (21.2\; m/s)t + 10.0\; m = 0 \ldotp\) Use of the quadratic formula yields t = 3.79 s and t = 0.54 s. Since the ball is at a height of 10 m at two times during its trajectory—once on the way up and once on the way down—we take the longer solution for the time it takes the ball to reach the spectator: \(t = 3.79\; s \ldotp\) The time for projectile motion is determined completely by the vertical motion. Thus, any projectile that has an initial vertical velocity of 21.2 m/s and lands 10.0 m above its starting altitude spends 3.79 s in the air.
2. We can find the final horizontal and vertical velocities v_x and v_y with the use of the result from (a). Then, we can combine them to find the magnitude of the total velocity vector \(\vec{v}\) and the angle \(\theta\) it makes with the horizontal. Since v_x is constant, we can solve for it at any horizontal location. We choose the starting point because we know both the initial velocity and the initial angle. Therefore, \(v_{x} = v_{0} \cos \theta_{0} = (30\; m/s) \cos 45^{o} = 21.2\; m/s \ldotp\) The final vertical velocity is given by Equation \ref{4.21}: \(v_{y} = v_{0y} - gt \ldotp\) Since \(v_{0y}\) was found in part (a) to be 21.2 m/s, we have \(v_{y} = 21.2\; m/s - (9.8\; m/s^{2})(3.79 s) = -15.9\; m/s \ldotp\) The magnitude of the final velocity \(\vec{v}\) is \(v = \sqrt{v_{x}^{2} + v_{y}^{2}} = \sqrt{(21.2\; m/s)^{2} + (-15.9\; m/s)^{2}} = 26.5\; m/s \ldotp\) The direction \(\theta_{v}\) is found using the inverse tangent: \(\theta_{v} = \tan^{-1} \left(\dfrac{v_{y}}{v_{x}}\right) = \tan^{-1} \left(\dfrac{21.2}{-15.9}\right) = -53.1^{o} \ldotp\)

Significance

1. As mentioned earlier, the time for projectile motion is determined completely by the vertical motion. Thus, any projectile that has an initial vertical velocity of 21.2 m/s and lands 10.0 m above its starting altitude spends 3.79 s in the air.
2. The negative angle means the velocity is 53.1° below the horizontal at the point of impact. This result is consistent with the fact that the ball is impacting at a point on the other side of the apex of the trajectory and therefore has a negative y component of the velocity. The magnitude of the velocity is less than the magnitude of the initial velocity we expect since it is impacting 10.0 m above the launch elevation.

Example \(\PageIndex{5}\): Time of Flight for a Projectile on a Horizontal Surface

Solve for the time of flight of a projectile that is both launched and impacts on a flat horizontal surface.

Solution

We can solve for the time of flight of a projectile that is both launched and impacts on a flat horizontal surface by performing some manipulations of the kinematic equations. We note the position and displacement in y must be zero at launch and at impact on an even surface. Thus, we set the displacement in y equal to zero and find

\[y - y_{0} = v_{0y} t - \frac{1}{2} gt^{2} = (v_{0} \sin \theta_{0})t - \frac{1}{2} gt^{2} = 0 \ldotp\]

Factoring, we have

\[t \left(v_{0} \sin \theta_{0} - \dfrac{gt}{2}\right) = 0 \ldotp\]

Solving for t gives us

\[t_{tof} = \frac{2(v_{0} \sin \theta_{0})}{g} \ldotp \label{4.24}\]

This is the time of flight for a projectile both launched and impacting on a flat horizontal surface. Equation \ref{4.24} does not apply when the projectile lands at a different elevation than it was launched, as we saw in Example 4.8 of the tennis player hitting the ball into the stands. The other solution, t = 0, corresponds to the time at launch. The time of flight is linearly proportional to the initial velocity in the y direction and inversely proportional to g. Thus, on the Moon, where gravity is one-sixth that of Earth, a projectile launched with the same velocity as on Earth would be airborne six times as long.

Example \(\PageIndex{5}\): Trajectory of a Projectile on a Horizontal Surface

Find an expression for the trajectory of a projectile

Solution

The trajectory of a projectile can be found by eliminating the time variable t from the kinematic equations for arbitrary t and solving for y(x). We take x₀ = y₀ = 0 so the projectile is launched from the origin. The kinematic equation for x gives

\[x = v_{0x}t \Rightarrow t = \frac{x}{v_{0x}} = \frac{x}{v_{0} \cos \theta_{0}} \ldotp\]

Substituting the expression for t into the equation for the position y = (v₀ sin \(\theta_{0}\))t - \(\frac{1}{2}\) gt² gives

\[y = (v_{0} \sin \theta_{0}) \left(\dfrac{x}{v_{0} \cos \theta_{0}}\right) - \frac{1}{2} g \left(\dfrac{x}{v_{0} \cos \theta_{0}}\right)^{2} \ldotp\]

Rearranging terms, we have

\[y = (\tan \theta_{0})x - \Big[ \frac{g}{2(v_{0} \cos \theta_{0})^{2}} \Big] x^{2} \ldotp \label{4.25}\]

This trajectory equation is of the form y = ax + bx², which is an equation of a parabola with coefficients

\[a = \tan \theta_{0}, \quad b = - \frac{g}{2(v_{0} \cos \theta_{0})^{2}} \ldotp\]

Orbit

When we speak of the range of a projectile on level ground, we assume R is very small compared with the circumference of Earth. If, however, the range is large, Earth curves away below the projectile and the acceleration resulting from gravity changes direction along the path. The range is larger than predicted by the range equation given earlier because the projectile has farther to fall than it would on level ground, as shown in Figure \(\PageIndex{7}\), which is based on a drawing in Newton’s Principia. If the initial speed is great enough, the projectile goes into orbit. Earth’s surface drops 5 m every 8000 m. In 1 s an object falls 5 m without air resistance. Thus, if an object is given a horizontal velocity of 8000 m/s (or 18,000 mi/hr) near Earth’s surface, it will go into orbit around the planet because the surface continuously falls away from the object. This is roughly the speed of the Space Shuttle in a low Earth orbit when it was operational, or any satellite in a low Earth orbit. These and other aspects of orbital motion, such as Earth’s rotation, are covered in another chapter.

Figure \(\PageIndex{7}\): Projectile to satellite. In each case shown here, a projectile is launched from a very high tower to avoid air resistance. With increasing initial speed, the range increases and becomes longer than it would be on level ground because Earth curves away beneath its path. With a speed of 8000 m/s, orbit is achieved.