4.2: Displacement and Velocity Vectors
( \newcommand{\kernel}{\mathrm{null}\,}\)
- Calculate position vectors in a multidimensional displacement problem.
- Solve for the displacement in two or three dimensions.
- Calculate the velocity vector given the position vector as a function of time.
- Calculate the average velocity in multiple dimensions.
Displacement and velocity in two or three dimensions are straightforward extensions of the one-dimensional definitions. However, now they are vector quantities, so calculations with them have to follow the rules of vector algebra, not scalar algebra.
Displacement Vector
To describe motion in two and three dimensions, we must first establish a coordinate system and a convention for the axes. We generally use the coordinates x, y, and z to locate a particle at point P(x,y,z) in three dimensions. If the particle is moving, the variables x, y, and z are functions of time (t):
x=x(t)y=y(t)z=z(t).
The position vector from the origin of the coordinate system to point P is →r(t). In unit vector notation, introduced in Coordinate Systems and Components of a Vector, →r(t) is
→r(t)=x(t)ˆi+y(t)ˆj+z(t)ˆk.
Figure 4.2.1 shows the coordinate system and the vector to point P, where a particle could be located at a particular time t. Note the orientation of the x, y, and z axes. This orientation is called a right-handed coordinate system and it is used throughout the chapter.
With our definition of the position of a particle in three-dimensional space, we can formulate the three-dimensional displacement. Figure 4.2.3 shows a particle at time t1 located at P1 with position vector →r(t1). At a later time t2, the particle is located at P2 with position vector →r(t2). The displacement vector Δ→r is found by subtracting →r(t1) from →r(t2):
Δ→r=→r(t2)−→r(t1).
Vector addition is discussed in Vectors. Note that this is the same operation we did in one dimension, but now the vectors are in three-dimensional space.
The following examples illustrate the concept of displacement in multiple dimensions
A satellite is in a circular polar orbit around Earth at an altitude of 400 km—meaning, it passes directly overhead at the North and South Poles. What is the magnitude and direction of the displacement vector from when it is directly over the North Pole to when it is at −45° latitude?
Strategy
We make a picture of the problem to visualize the solution graphically. This will aid in our understanding of the displacement. We then use unit vectors to solve for the displacement.
Solution
Figure 4.2.3 shows the surface of Earth and a circle that represents the orbit of the satellite. Although satellites are moving in three-dimensional space, they follow trajectories of ellipses, which can be graphed in two dimensions. The position vectors are drawn from the center of Earth, which we take to be the origin of the coordinate system, with the y-axis as north and the x-axis as east. The vector between them is the displacement of the satellite. We take the radius of Earth as 6370 km, so the length of each position vector is 6770 km.
In unit vector notation, the position vectors are
→r(t1)=6770.kmˆj→r(t2)=6770.km(cos(−45°))ˆi+6770.km(sin(−45°))ˆj.
Evaluating the sine and cosine, we have
→r(t1)=6770.ˆj→r(t2)=4787ˆi−4787ˆj.
Now we can find Δ→r, the displacement of the satellite:
Δ→r=→r(t2)−→r(t1)=4787ˆi−11,557ˆj.
The magnitude of the displacement is
|Δ→r|=√(4787)2+(−11,557)2=12,509km.
The angle the displacement makes with the x-axis is
θ=tan−1(−11,5574787)=−67.5o.
Significance
Plotting the displacement gives information and meaning to the unit vector solution to the problem. When plotting the displacement, we need to include its components as well as its magnitude and the angle it makes with a chosen axis—in this case, the x-axis (Figure 4.2.4).
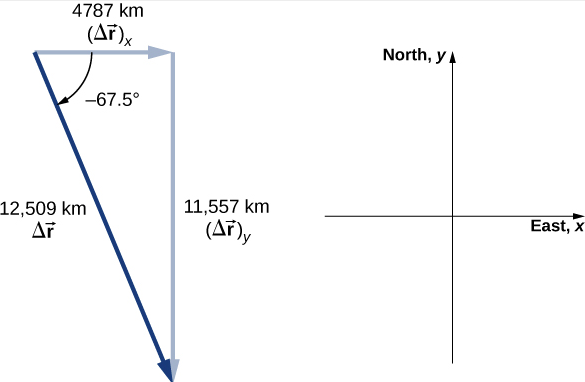
Note that the satellite took a curved path along its circular orbit to get from its initial position to its final position in this example. It also could have traveled 4787 km east, then 11,557 km south to arrive at the same location. Both of these paths are longer than the length of the displacement vector. In fact, the displacement vector gives the shortest path between two points in one, two, or three dimensions.
Many applications in physics can have a series of displacements, as discussed in the previous chapter. The total displacement is the sum of the individual displacements, only this time, we need to be careful, because we are adding vectors. We illustrate this concept with an example of Brownian motion.
Brownian motion is a chaotic random motion of particles suspended in a fluid, resulting from collisions with the molecules of the fluid. This motion is three-dimensional. The displacements in numerical order of a particle undergoing Brownian motion could look like the following, in micrometers (Figure 4.2.5):
Δ→r1=2.0ˆi+ˆj+3.0ˆk
Δ→r2=−ˆi+3.0ˆk
Δ→r3=4.0ˆi−2.0ˆj+ˆk
Δ→r4=−3.0ˆi+ˆj+3.0ˆk.
What is the total displacement of the particle from the origin?
Solution
We form the sum of the displacements and add them as vectors:
Δ→rTotal=∑Δ→ri=Δ→r1+Δ→r2+Δ→r3+Δ→r4=(2.0−1.0+4.0−3.0)ˆi+(1.0+0−2.0+1.0)ˆj+(3.0+3.0+1.0+2.0)ˆk=2.0ˆi+0ˆj+9.0ˆkμm.
To complete the solution, we express the displacement as a magnitude and direction,
|Δ→rTotal|=√2.02+02+9.02=9.2μm,θ=tan−1(92)=77o,
with respect to the x-axis in the xz-plane.
Significance
From the figure we can see the magnitude of the total displacement is less than the sum of the magnitudes of the individual displacements.
Velocity Vector
In the previous chapter we found the instantaneous velocity by calculating the derivative of the position function with respect to time. We can do the same operation in two and three dimensions, but we use vectors. The instantaneous velocity vector is now
→v(t)=lim
Let’s look at the relative orientation of the position vector and velocity vector graphically. In Figure \PageIndex{6} we show the vectors \vec{r}(t) and \vec{r}(t + \Deltat), which give the position of a particle moving along a path represented by the gray line. As \Deltat goes to zero, the velocity vector, given by Equation \ref{4.4}, becomes tangent to the path of the particle at time t.
Equation \ref{4.4} can also be written in terms of the components of \vec{v}(t). Since
\vec{r} (t) = x(t)\; \hat{i} + y(t)\; \hat{j} + z(t)\; \hat{k},
we can write
\vec{v} (t) = v_{x} (t)\; \hat{i} + v_{y} (t)\; \hat{j} + v_{z} (t)\; \hat{k} \label{4.5}
where
v_{x} (t) = \frac{dx(t)}{dt}, \quad v_{y} (t) = \frac{dy(t)}{dt}, \quad v_{z} (t) = \frac{dz(t)}{dt} \ldotp \label{4.6}
If only the average velocity is of concern, we have the vector equivalent of the one-dimensional average velocity for two and three dimensions:
\vec{v}_{avg} = \frac{\vec{r} (t_{2}) - \vec{r} (t_{1})}{t_{2} - t_{1}} \ldotp \label{4.7}
The position function of a particle is \vec{r}(t) = 2.0t2 \hat{i} + (2.0 + 3.0t) \hat{j}+ 5.0t \hat{k} m. (a) What is the instantaneous velocity and speed at t = 2.0 s? (b) What is the average velocity between 1.0 s and 3.0 s?
Solution
Using Equation \ref{4.5} and Equation \ref{4.6}, and taking the derivative of the position function with respect to time, we find
- v(t) = \frac{d\vec{r} (t)}{dt} = 4.0t\; \hat{i} + 3.0\; \hat{j} + 5.0\; \hat{k}\; m/s\vec{v} (2.0\; s) = 8.0\; \hat{i} + 3.0\; \hat{j} + 5.0\; \hat{k}\; m/sSpeed\; |\vec{v} (2.0\; s)| = \sqrt{8^{2} + 3^{2} + 5^{2}} = 9.9\; m/s \ldotp
- From Equation \ref{4.7}, \begin{split} \vec{v}_{avg} & = \frac{\vec{r} (t_{2}) - \vec{r} (t_{1})}{t_{2} - t_{1}} = \frac{\vec{r} (3.0\;s ) - \vec{r} (1.0\; s)}{3.0\; s - 1.0\; s} = \frac{(18\; \hat{i} + 11\; \hat{j} + 15\; \hat{k}) m - (2\; \hat{i} + 5\; \hat{j} + 5\; \hat{k}) m}{2.0\; s} \\ & = \frac{(16\; \hat{i} + 6\; \hat{j} + 10\; \hat{k}) m}{2.0\; s} = 8.0\; \hat{i} + 3.0\; \hat{j} + 5.0\; \hat{k}\; m/s \ldotp \end{split}
Significance
We see the average velocity is the same as the instantaneous velocity at t = 2.0 s, as a result of the velocity function being linear. This need not be the case in general. In fact, most of the time, instantaneous and average velocities are not the same.
The position function of a particle is \vec{r}(t) = 3.0t3 \hat{i} + 4.0 \hat{j}. (a) What is the instantaneous velocity at t = 3 s? (b) Is the average velocity between 2 s and 4 s equal to the instantaneous velocity at t = 3 s?
The Independence of Perpendicular Motions
When we look at the three-dimensional equations for position and velocity written in unit vector notation, Equation \ref{4.2} and Equation \ref{4.5}, we see the components of these equations are separate and unique functions of time that do not depend on one another. Motion along the x direction has no part of its motion along the y and z directions, and similarly for the other two coordinate axes. Thus, the motion of an object in two or three dimensions can be divided into separate, independent motions along the perpendicular axes of the coordinate system in which the motion takes place.
To illustrate this concept with respect to displacement, consider a woman walking from point A to point B in a city with square blocks. The woman taking the path from A to B may walk east for so many blocks and then north (two perpendicular directions) for another set of blocks to arrive at B. How far she walks east is affected only by her motion eastward. Similarly, how far she walks north is affected only by her motion northward.
In the kinematic description of motion, we are able to treat the horizontal and vertical components of motion separately. In many cases, motion in the horizontal direction does not affect motion in the vertical direction, and vice versa.
An example illustrating the independence of vertical and horizontal motions is given by two baseballs. One baseball is dropped from rest. At the same instant, another is thrown horizontally from the same height and it follows a curved path. A stroboscope captures the positions of the balls at fixed time intervals as they fall (Figure \PageIndex{7}).
It is remarkable that for each flash of the strobe, the vertical positions of the two balls are the same. This similarity implies vertical motion is independent of whether the ball is moving horizontally. (Assuming no air resistance, the vertical motion of a falling object is influenced by gravity only, not by any horizontal forces.) Careful examination of the ball thrown horizontally shows it travels the same horizontal distance between flashes. This is because there are no additional forces on the ball in the horizontal direction after it is thrown. This result means horizontal velocity is constant and is affected neither by vertical motion nor by gravity (which is vertical). Note this case is true for ideal conditions only. In the real world, air resistance affects the speed of the balls in both directions.
The two-dimensional curved path of the horizontally thrown ball is composed of two independent one-dimensional motions (horizontal and vertical). The key to analyzing such motion, called projectile motion, is to resolve it into motions along perpendicular directions. Resolving two-dimensional motion into perpendicular components is possible because the components are independent.


