4.1: Forces
( \newcommand{\kernel}{\mathrm{null}\,}\)
- Distinguish between kinematics and dynamics
- Understand the definition of force
- Identify simple free-body diagrams
- Define the SI unit of force, the newton
- Describe force as a vector
- Define pressure and its related SI units
- Explain the relationship between pressure and force
- Calculate force given pressure and area
- Distinguish between real and fictitious forces
The study of motion is called kinematics, but kinematics only describes the way objects move—their velocity and their acceleration. Dynamics is the study of how forces affect the motion of objects and systems. It considers the causes of motion of objects and systems of interest. A system is anything being analyzed, it can be made up of one or many objects. In this chapter, we start focusing on dynamics by exploring the various forces that can affect motion. We will discuss how these forces affect motion later.
Introduction to Forces
Forces affect every moment of our life. Sometimes, they help things stay in place, and other cases Your body is held to Earth by force and held together by the forces of charged particles. When you open a door, walk down a street, lift your fork, or touch a baby’s face, you are applying forces. Zooming in deeper, your body’s atoms are held together by electrical forces, and the core of the atom, called the nucleus, is held together by the strongest force we know—strong nuclear force.
Working Definition of Force
When thinking of force, we often think of a push or a pull. We know that a push or a pull has both magnitude and direction (therefore, it is a vector quantity), so we can define force as the push or pull on an object with a specific magnitude and direction. Force can be represented by vectors or expressed as a multiple of a standard force.
The push or pull on an object can vary considerably in either magnitude or direction. For example, a cannon exerts a strong force on a cannonball that is launched into the air. In contrast, Earth exerts only a tiny downward pull on a flea. Our everyday experiences also give us a good idea of how multiple forces add. If two people push in different directions on a third person, as illustrated in Figure \PageIndex{3}, we might expect the total force to be in the direction shown. Since force is a vector, it adds just like other vectors. Forces, like other vectors, are represented by arrows and can be added using the familiar head-to-tail method or trigonometric methods. These ideas were developed in Vectors.
Figure \PageIndex{2}(b) is our first example of a free-body diagram, which is a sketch showing all external forces acting on an object or system. The object or system is represented by a single isolated point (or free body), and only those forces acting on it that originate outside of the object or system—that is, external forces—are shown. (These forces are the only ones shown because only external forces acting on the free body affect its motion. We can ignore any internal forces within the body.) The forces are represented by vectors extending outward from the free body.
Development of the Force Concept
A quantitative definition of force can be based on some standard force, just as distance is measured in units relative to a standard length. One possibility is to stretch a spring a certain fixed distance (Figure \PageIndex{4}) and use the force it exerts to pull itself back to its relaxed shape—called a restoring force—as a standard. The magnitude of all other forces can be considered as multiples of this standard unit of force. Many other possibilities exist for standard forces. Some alternative definitions of force will be given later in this chapter.
Let’s analyze force more deeply. Suppose a physics student sits at a table, working diligently on his homework (Figure \PageIndex{5}). What external forces act on him? Can we determine the origin of these forces?
In most situations, forces are grouped into two categories: contact forces and field forces. As you might guess, contact forces are due to direct physical contact between objects. For example, the student in Figure \PageIndex{5} experiences the contact forces \vec{C}, \vec{F}, and \vec{T}, which are exerted by the chair on his posterior, the floor on his feet, and the table on his forearms, respectively. Field forces, however, act without the necessity of physical contact between objects. They depend on the presence of a “field” in the region of space surrounding the body under consideration. Since the student is in Earth’s gravitational field, he feels a gravitational force \vec{w}; in other words, he has weight.
You can think of a field as a property of space that is detectable by the forces it exerts. Scientists think there are only four fundamental force fields in nature. These are the gravitational, electromagnetic, strong nuclear, and weak fields (we consider these four forces in nature later in this text). As noted for \vec{w} in Figure \PageIndex{5}, the gravitational field is responsible for the weight of a body. The forces of the electromagnetic field include those of static electricity and magnetism; they are also responsible for the attraction among atoms in bulk matter. Both the strong nuclear and the weak force fields are effective only over distances roughly equal to a length of scale no larger than an atomic nucleus (10−15 m). Their range is so small that neither field has influence in the macroscopic world of Newtonian mechanics.
Contact forces are fundamentally electromagnetic. While the elbow of the student in Figure \PageIndex{5} is in contact with the tabletop, the atomic charges in his skin interact electromagnetically with the charges in the surface of the table. The net (total) result is the force \vec{T}. Similarly, when adhesive tape sticks to a piece of paper, the atoms of the tape are intermingled with those of the paper to cause a net electromagnetic force between the two objects. However, in the context of Newtonian mechanics, the electromagnetic origin of contact forces is not an important concern.
Vector Notation for Force
As previously discussed, force is a vector; it has both magnitude and direction. The SI unit of force is called the newton (abbreviated N), and 1 N is the force needed to accelerate an object with a mass of 1 kg at a rate of 1 m/s2: 1 N = 1 kg • m/s2. An easy way to remember the size of a newton is to imagine holding a small apple; it has a weight of about 1 N.
We can thus describe a two-dimensional force in the form \vec{F} = a \hat{i} + b \hat{j} (the unit vectors \hat{i} and \hat{j} indicate the direction of these forces along the x-axis and the y-axis, respectively) and a three-dimensional force in the form \vec{F} = a \hat{i} + b \hat{j} + c \hat{k}. In Figure \PageIndex{2}, let’s suppose that ice skater 1, on the left side of the figure, pushes horizontally with a force of 30.0 N to the right; we represent this as \vec{F}_{1} = 30.0 \hat{i} N. Similarly, if ice skater 2 pushes with a force of 40.0 N in the positive vertical direction shown, we would write \vec{F}_{2} = 40.0 \hat{j} N. The resultant of the two forces causes a mass to accelerate—in this case, the third ice skater. This resultant is called the net external force \vec{F}_{net} and is found by taking the vector sum of all external forces acting on an object or system (thus, we can also represent net external force as \sum\vec{F}):
\vec{F}_{net} = \sum\vec{F} = \vec{F}_{1} + \vec{F}_{2} + \ldots \label{5.1}
This equation can be extended to any number of forces.
In this example, we have \vec{F}_{net} = \sum \vec{F} = \vec{F}_{1} + \vec{F}_{2} = 30.0 \hat{i} + 40.0 \hat{j}. The hypotenuse of the triangle shown in Figure \PageIndex{2} is the resultant force, or net force. It is a vector. To find its magnitude (the size of the vector, without regard to direction), we use the rule given in Vectors, taking the square root of the sum of the squares of the components:
\vec{F}_{net} = \sqrt{(30.0\; N)^{2} + (40.0\; N)^{2}} = 50.0\; N \ldotp
The direction is given by
\theta = \tan^{-1} \left(\dfrac{F_{2}}{F_{1}}\right) = \tan^{-1} \left(\dfrac{40.0}{30.0}\right) = 53.1^{o},
measured from the positive x-axis, as shown in the free-body diagram in Figure \PageIndex{2}(b).
Let’s suppose the ice skaters now push the third ice skater with \vec{F}_{1} = 3.0 \hat{i} + 8.0 \hat{j} N and \vec{F}_{2} = 5.0 \hat{i} + 4.0 \hat{j} N. What is the resultant of these two forces? We must recognize that force is a vector; therefore, we must add using the rules for vector addition:
\vec{F}_{net} = \vec{F}_{1} + \vec{F}_{2} = \big(3.0 \hat{i} + 8.0 \hat{j} \big) + \big(5.0 \hat{i} + 4.0 \hat{j} \big) = 8.0 \hat{i} + 12 \hat{j}\; N
Pressure
You have no doubt heard the word ‘pressure’ used in relation to blood (high or low blood pressure) and in relation to weather (high- and low-pressure weather systems). These are only two of many examples of pressure in fluids.
Pressure (p) is defined as the normal force F per unit area A over which the force is applied, or
p = \frac{|\vec{F}|}{A} \ldotp \label{14.3}
To define the pressure at a specific point, the pressure is defined as the force dF exerted by a fluid over an infinitesimal element of area dA containing the point, resulting in p = |\frac{d\vec{F}}{dA}|.
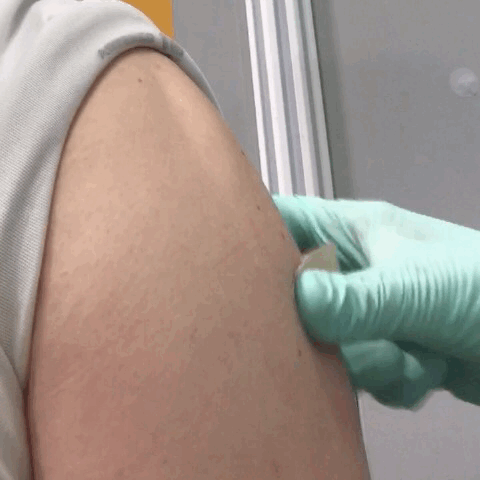
A given force can have a significantly different effect, depending on the area over which the force is exerted. For instance, a force applied to an area of 1 mm2 has a pressure that is 100 times as great as the same force applied to an area of 1 cm2 . That is why a sharp needle is able to poke through skin when a small force is exerted, but applying the same force with a finger does not puncture the skin (Figure \PageIndex{4}).
 |
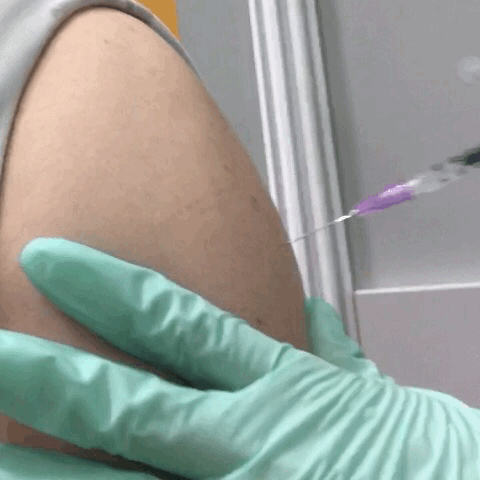 |
Figure \PageIndex{4}: (a) A person being poked with a finger might be irritated, but the force has little lasting effect. (b) In contrast, the same force applied to an area the size of the sharp end of a needle is enough to break the skin.
Note that although force is a vector, pressure is a scalar. Pressure is a scalar quantity because it is defined to be proportional to the magnitude of the force acting perpendicular to the surface area. The SI unit for pressure is the pascal (Pa), named after the French mathematician and physicist Blaise Pascal (1623–1662), where
1\; Pa = 1\; N/m^{2} \ldotp
Real Forces and Inertial Frames
There is another distinction among forces: Some forces are real, whereas others are not. Real forces have some physical origin, such as a gravitational pull. In contrast, fictitious forces arise simply because an observer is in an accelerating or noninertial frame of reference, such as one that rotates (like a merry-go-round) or undergoes linear acceleration (like a car slowing down). For example, if a satellite is heading due north above Earth’s Northern Hemisphere, then to an observer on Earth, it will appear to experience a force to the west that has no physical origin. Instead, Earth is rotating toward the east and moves east under the satellite. In Earth’s frame, this looks like a westward force on the satellite, or it can be interpreted as a violation of Newton’s first law (the law of inertia). We can identify a fictitious force by asking the question, “What is the reaction force?” If we cannot name the reaction force, then the force we are considering is fictitious. In the example of the satellite, the reaction force would have to be an eastward force on Earth. Recall that an inertial frame of reference is one in which all forces are real and, equivalently, one in which Newton’s laws have the simple forms given in this chapter.
Earth’s rotation is slow enough that Earth is nearly an inertial frame. You ordinarily must perform precise experiments to observe fictitious forces and the slight departures from Newton’s laws, such as the effect just described. On a large scale, such as for the rotation of weather systems and ocean currents, the effects can be easily observed (Figure \PageIndex{10}).
The crucial factor in determining whether a frame of reference is inertial is whether it accelerates or rotates relative to a known inertial frame. Unless stated otherwise, all phenomena discussed in this text are in inertial frames.
External Forces, Net Force and Resultant
An external force is a force acting on an object or system of objects that originates outside of the object or the system. An intuitive notion of external is correct—it is outside the system of interest. For example, in Figure \PageIndex{1a}, the system of interest is the car plus the person within it. The two forces exerted by the two students are external forces. In contrast, an internal force acts between elements of the system. Thus, the force the person in the car exerts to hang on to the steering wheel is an internal force between elements of the system of interest. Any forces exerted by the engine of the car are also internal forces. We will learn later that only external forces affect the motion of a system. Therefore, to determine which forces are external, we must define the boundaries of the system of objects. Sometimes, the system is obvious, whereas at other times, identifying the boundaries of a system is more subtle.
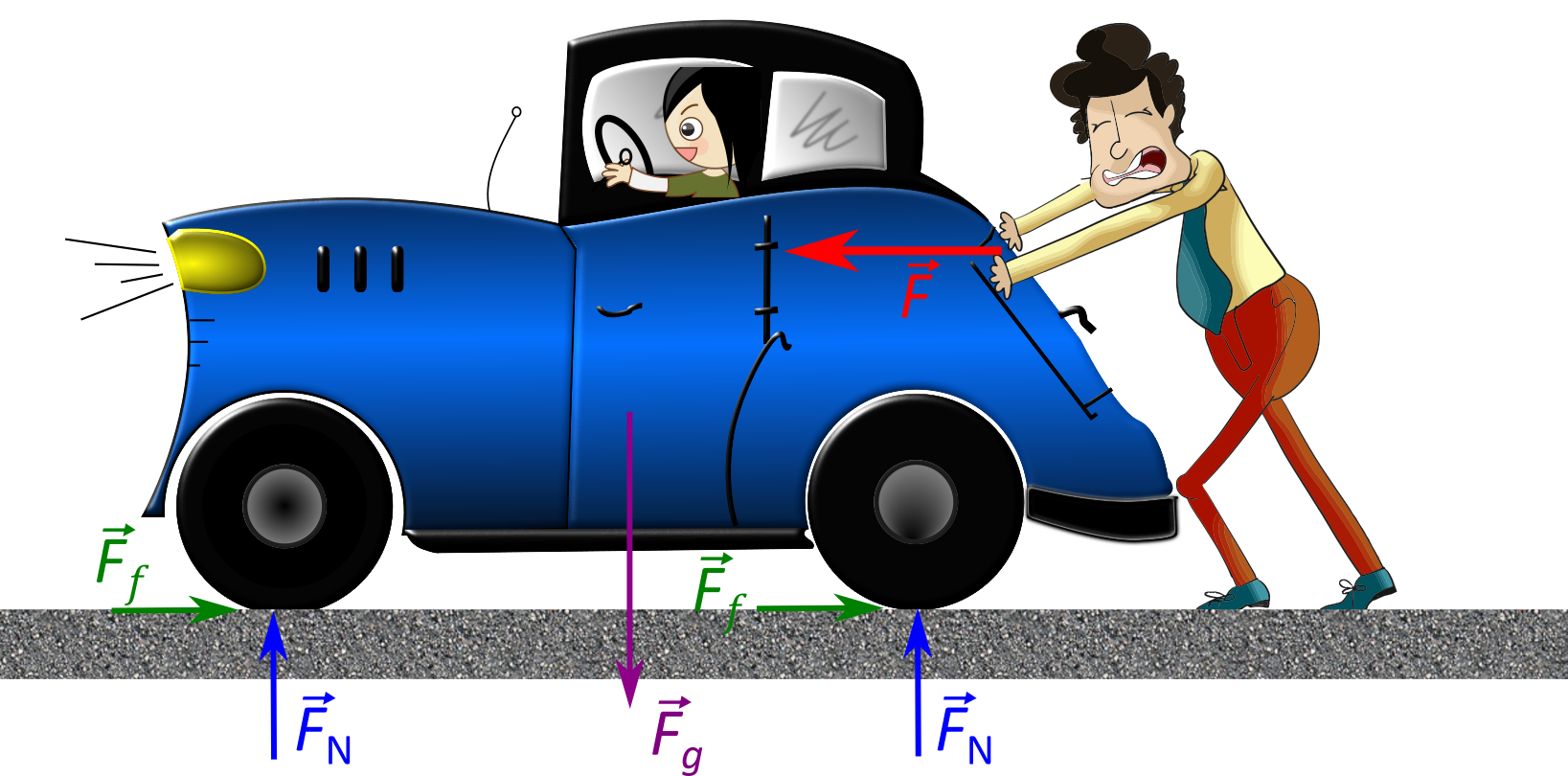
From this example, you can see that different forces exerted on the same mass produce different accelerations. In Figure \PageIndex{1a}, the two students push a car with a driver in it. Arrows representing all external forces are shown. The system of interest is the car and its driver. The weight \vec{w} of the system and the support of the ground \vec{N} are also shown for completeness and are assumed to cancel (because there was no vertical motion and no imbalance of forces in the vertical direction to create a change in motion). The vector \vec{f} represents the friction acting on the car, and it acts to the left, opposing the motion of the car. (We discuss friction in more detail in the next chapter.) In Figure \PageIndex{1b}, all external forces acting on the system add together to produce the net force \vec{F}_{net}. The free-body diagram shows all of the forces acting on the system of interest. The dot represents the center of mass of the system. Each force vector extends from this dot. Because there are two forces acting to the right, the vectors are shown collinearly. Finally, in Figure \PageIndex{1c}, a larger net external force produces a larger acceleration (\vec{a}' > \vec{a}) when the tow truck pulls the car.
It seems reasonable that acceleration would be directly proportional to and in the same direction as the net external force acting on a system. This assumption has been verified experimentally and is illustrated in Figure \PageIndex{1}. To obtain an equation for Newton’s second law, we first write the relationship of acceleration \vec{a} and net external force \vec{F}_{net} as the proportionality
\vec{a}\; \propto\; \vec{F}_{net}
where the symbol \alpha means “proportional to.” (Recall from Forces that the net external force is the vector sum of all external forces and is sometimes indicated as \sum \vec{F}.) This proportionality shows what we have said in words—acceleration is directly proportional to net external force. Once the system of interest is chosen, identify the external forces and ignore the internal ones. It is a tremendous simplification to disregard the numerous internal forces acting between objects within the system, such as muscular forces within the students’ bodies, let alone the myriad forces between the atoms in the objects. Still, this simplification helps us solve some complex problems.
It also seems reasonable that acceleration should be inversely proportional to the mass of the system. In other words, the larger the mass (the inertia), the smaller the acceleration produced by a given force. As illustrated in Figure \PageIndex{2}, the same net external force applied to a basketball produces a much smaller acceleration when it is applied to an SUV. The proportionality is written as
a\; \propto\; \frac{1}{m},
It has been found that the acceleration of an object depends only on the net external force and the mass of the object. Combining the two proportionalities just given yields Newton’s second law.
The acceleration of a system is directly proportional to and in the same direction as the net external force acting on the system and is inversely proportion to its mass. In equation form, Newton’s second law is
\vec{a} = \frac{\vec{F}_{net}}{m},
where \vec{a} is the acceleration, \vec{F}_{net} is the net force, and m is the mass. This is often written in the more familiar form
\vec{F}_{net} = \sum \vec{F} = m \vec{a}, \label{5.3}
but the first equation gives more insight into what Newton’s second law means. When only the magnitude of force and acceleration are considered, this equation can be written in the simpler scalar form:
\vec{F}_{net} = ma \ldotp \label{5.4}
The law is a cause-and-effect relationship among three quantities that is not simply based on their definitions. The validity of the second law is based on experimental verification. The free-body diagram, which you will learn to draw in Drawing Free-Body Diagrams, is the basis for writing Newton’s second law.
Force and Acceleration
Before talking First, what do we mean by a change in motion? The answer is that a change in motion is equivalent to a change in velocity. A change in velocity means, by definition, that there is acceleration. Newton’s first law says that a net external force causes a change in motion; thus, we see that a net external force causes nonzero acceleration.
From this example, you can see that different forces exerted on the same mass produce different accelerations. In Figure \PageIndex{1a}, the two students push a car with a driver in it. Arrows representing all external forces are shown. The system of interest is the car and its driver. The weight \vec{w} of the system and the support of the ground \vec{N} are also shown for completeness and are assumed to cancel (because there was no vertical motion and no imbalance of forces in the vertical direction to create a change in motion). The vector \vec{f} represents the friction acting on the car, and it acts to the left, opposing the motion of the car. (We discuss friction in more detail in the next chapter.) In Figure \PageIndex{1b}, all external forces acting on the system add together to produce the net force \vec{F}_{net}. The free-body diagram shows all of the forces acting on the system of interest. The dot represents the center of mass of the system. Each force vector extends from this dot. Because there are two forces acting to the right, the vectors are shown collinearly. Finally, in Figure \PageIndex{1c}, a larger net external force produces a larger acceleration (\vec{a}' > \vec{a}) when the tow truck pulls the car.
It seems reasonable that acceleration would be directly proportional to and in the same direction as the net external force acting on a system. This assumption has been verified experimentally and is illustrated in Figure \PageIndex{1}. To obtain an equation for Newton’s second law, we first write the relationship of acceleration \vec{a} and net external force \vec{F}_{net} as the proportionality
\vec{a}\; \propto\; \vec{F}_{net}
where the symbol \alpha means “proportional to.” (Recall from Forces that the net external force is the vector sum of all external forces and is sometimes indicated as \sum \vec{F}.) This proportionality shows what we have said in words—acceleration is directly proportional to net external force. Once the system of interest is chosen, identify the external forces and ignore the internal ones. It is a tremendous simplification to disregard the numerous internal forces acting between objects within the system, such as muscular forces within the students’ bodies, let alone the myriad forces between the atoms in the objects. Still, this simplification helps us solve some complex problems.
It also seems reasonable that acceleration should be inversely proportional to the mass of the system. In other words, the larger the mass (the inertia), the smaller the acceleration produced by a given force. As illustrated in Figure \PageIndex{2}, the same net external force applied to a basketball produces a much smaller acceleration when it is applied to an SUV. The proportionality is written as
a\; \propto\; \frac{1}{m},
where m is the mass of the system and a is the magnitude of the acceleration. Experiments have shown that acceleration is exactly inversely proportional to mass, just as it is directly proportional to net external force.

It has been found that the acceleration of an object depends only on the net external force and the mass of the object. Combining the two proportionalities just given yields Newton’s second law.
The acceleration of a system is directly proportional to and in the same direction as the net external force acting on the system and is inversely proportion to its mass. In equation form, Newton’s second law is
\vec{a} = \frac{\vec{F}_{net}}{m},
where \vec{a} is the acceleration, \vec{F}_{net} is the net force, and m is the mass. This is often written in the more familiar form
\vec{F}_{net} = \sum \vec{F} = m \vec{a},
but the first equation gives more insight into what Newton’s second law means.
The law is a cause-and-effect relationship among three quantities that is not simply based on their definitions. The validity of the second law is based on experimental verification. The free-body diagram, which you will learn to draw in Drawing Free-Body Diagrams, is the basis for writing Newton’s second law.


