9.3: Rotational Kinetic Energy

Learning Objectives

• Describe the differences between rotational and translational kinetic energy
• Define the physical concept of moment of inertia in terms of the mass distribution from the rotational axis
• Explain how the moment of inertia of rigid bodies affects their rotational kinetic energy
• Use conservation of mechanical energy to analyze systems undergoing both rotation and translation
• Calculate the angular velocity of a rotating system when there are energy losses due to nonconservative forces

So far in this chapter, we have been working with rotational kinematics: the description of motion for a rotating rigid body with a fixed axis of rotation. In this section, we define two new quantities that are helpful for analyzing properties of rotating objects: moment of inertia and rotational kinetic energy. With these properties defined, we will have two important tools we need for analyzing rotational dynamics.

Rotational Kinetic Energy

Any moving object has kinetic energy. We know how to calculate this for a body undergoing translational motion, but how about for a rigid body undergoing rotation? This might seem complicated because each point on the rigid body has a different velocity. However, we can make use of angular velocity—which is the same for the entire rigid body—to express the kinetic energy for a rotating object. Figure \(\PageIndex{1}\) shows an example of a very energetic rotating body: an electric grindstone propelled by a motor. Sparks are flying, and noise and vibration are generated as the grindstone does its work. This system has considerable energy, some of it in the form of heat, light, sound, and vibration. However, most of this energy is in the form of rotational kinetic energy.

Figure \(\PageIndex{1}\): The rotational kinetic energy of the grindstone is converted to heat, light, sound, and vibration. (credit: Zachary David Bell, US Navy)

Energy in rotational motion is not a new form of energy; rather, it is the energy associated with rotational motion, the same as kinetic energy in translational motion. However, because kinetic energy is given by \(K=\frac{1}{2}mv^2\), and velocity is a quantity that is different for every point on a rotating body about an axis, it makes sense to find a way to write kinetic energy in terms of the variable \(\omega\), which is the same for all points on a rigid rotating body. For a single particle rotating around a fixed axis, this is straightforward to calculate. We can relate the angular velocity to the magnitude of the translational velocity using the relation \(v_t=\omega r\), where \(r\) is the distance of the particle from the axis of rotation and \(v_t\) is its tangential speed. Substituting into the equation for kinetic energy, we find

\[ K=\frac{1}{2} m v_{t}^{2}=\frac{1}{2} m(\omega r)^{2}=\frac{1}{2}\left(m r^{2}\right) \omega^{2}. \nonumber \]

In the case of a rigid rotating body, we can divide up any body into a large number of smaller masses, each with a mass \(m_j\) and distance to the axis of rotation \(r_j\), such that the total mass of the body is equal to the sum of the individual masses: \(M=\sum_{j} m_{j}\). Each smaller mass has tangential speed \(v_j\), where we have dropped the subscript \(t\) for the moment. The total kinetic energy of the rigid rotating body is

\[ K=\sum_{j} \frac{1}{2} m_{j} v_{j}^{2}=\sum_{j} \frac{1}{2} m_{j}\left(r_{j} \omega_{j}\right)^{2} \nonumber \]

and since \(\omega_j = \omega\) for all masses,

\[ K=\frac{1}{2}\left(\sum_{j} m_{j} r_{j}^{2}\right) \omega^{2} . \label{10.16} \]

The units of Equation \ref{10.16} are joules (J). The equation in this form is complete, but awkward; we need to find a way to generalize it.

The moment of inertia is the quantitative measure of rotational inertia, just as in translational motion, and mass is the quantitative measure of linear inertia—that is, the more massive an object is, the more inertia it has, and the greater is its resistance to change in linear velocity. Similarly, the greater the moment of inertia of a rigid body or system of particles, the greater is its resistance to change in angular velocity about a fixed axis of rotation. It is interesting to see how the moment of inertia varies with r, the distance to the axis of rotation of the mass particles in Equation \ref{10.17}. Rigid bodies and systems of particles with more mass concentrated at a greater distance from the axis of rotation have greater moments of inertia than bodies and systems of the same mass, but concentrated near the axis of rotation. In this way, we can see that a hollow cylinder has more rotational inertia than a solid cylinder of the same mass when rotating about an axis through the center. Substituting Equation \ref{10.17} into Equation \ref{10.16}, the expression for the kinetic energy of a rotating rigid body becomes

\[ K=\frac{1}{2} I \omega^{2} . \label{10.18} \]

We see from this equation that the kinetic energy of a rotating rigid body is directly proportional to the moment of inertia and the square of the angular velocity. This is exploited in flywheel energy-storage devices, which are designed to store large amounts of rotational kinetic energy. Many carmakers are now testing flywheel energy storage devices in their automobiles, such as the flywheel, or kinetic energy recovery system, shown in Figure \(\PageIndex{2}\).

Figure \(\PageIndex{2}\): A KERS (kinetic energy recovery system) flywheel used in cars. (credit: “cmonville”/Flickr)

The rotational and translational quantities for kinetic energy and inertia are summarized in Table 10.4. The relationship column is not included because a constant doesn’t exist by which we could multiply the rotational quantity to get the translational quantity, as can be done for the variables in Table 10.3.

Table 10.4: Rotational and Translational Kinetic Energies and Inertia

Rotational	Translational
\(I=\sum_{j} m_{j} r_{j}^{2}\)	\(m\)
\(K = \frac{1}{2}I \omega^2\)	\(K = \frac{1}{2} m v^2 \)

Example \(\PageIndex{1}\): Moment of Inertia of a system of particles

Six small washers are spaced 10 cm apart on a rod of negligible mass and 0.5 m in length. The mass of each washer is 20 g. The rod rotates about an axis located at 25 cm, as shown in Figure \(\PageIndex{3}\). (a) What is the moment of inertia of the system? (b) If the two washers closest to the axis are removed, what is the moment of inertia of the remaining four washers? (c) If the system with six washers rotates at 5 rev/s, what is its rotational kinetic energy?

Figure \(\PageIndex{3}\): Six washers are spaced 10 cm apart on a rod of negligible mass and rotating about a vertical axis.

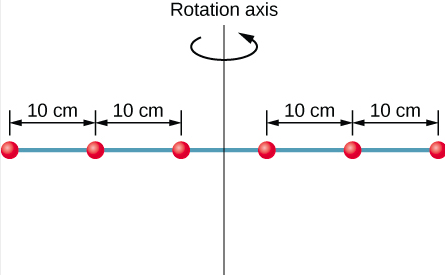
Strategy

1. We use the definition for moment of inertia for a system of particles and perform the summation to evaluate this quantity. The masses are all the same so we can pull that quantity in front of the summation symbol.
2. We do a similar calculation.
3. We insert the result from (a) into the expression for rotational kinetic energy.

Solution

1. \(I=\sum m_{j} r_{j}^{2}=(0.02 \: \mathrm{kg})\left(2 \times(0.25 \: \mathrm{m})^{2}+2 \times(0.15 \: \mathrm{m})^{2}+2 \times(0.05 \: \mathrm{m})^{2}\right)=0.0035 \: \mathrm{kg} \cdot \mathrm{m}^{2}\)
2. \(I=\sum_{j} m_{j} r_{j}^{2}=(0.02 \: \mathrm{kg})\left(2 \times(0.25 \: \mathrm{m})^{2}+2 \times(0.15 \: \mathrm{m})^{2}\right)=0.0034 \: \mathrm{kg} \cdot \mathrm{m}^{2}\)
3. \(K=\frac{1}{2} I \omega^{2}=\frac{1}{2}\left(0.0035 \: \mathrm{kg} \cdot \mathrm{m}^{2}\right)(5.0 \times 2 \pi \: \mathrm{rad} / \mathrm{s})^{2}=1.73 \: \mathrm{J}\)

Significance

We can see the individual contributions to the moment of inertia. The masses close to the axis of rotation have a very small contribution. When we removed them, it had a very small effect on the moment of inertia.

Applying Rotational Kinetic Energy

Now let’s apply the ideas of rotational kinetic energy and the moment of inertia table to get a feeling for the energy associated with a few rotating objects. The following examples will also help get you comfortable using these equations. First, let’s look at a general problem-solving strategy for rotational energy.

PROBLEM-SOLVING STRATEGY: ROTATIONAL ENERGY

1. Determine that energy or work is involved in the rotation.
2. Determine the system of interest. A sketch usually helps.
3. Analyze the situation to determine the types of work and energy involved.
4. If there are no losses of energy due to friction and other nonconservative forces, mechanical energy is conserved, that is, \(K_i + U_i = K_f + U_f\).
5. If nonconservative forces are present, mechanical energy is not conserved, and other forms of energy, such as heat and light, may enter or leave the system. Determine what they are and calculate them as necessary.
6. Eliminate terms wherever possible to simplify the algebra.
7. Evaluate the numerical solution to see if it makes sense in the physical situation presented in the wording of the problem.

Example \(\PageIndex{2}\): Calculating helicopter energies

A typical small rescue helicopter has four blades: Each is 4.00 m long and has a mass of 50.0 kg (Figure \(\PageIndex{5}\)). The blades can be approximated as thin rods that rotate about one end of an axis perpendicular to their length. The helicopter has a total loaded mass of 1000 kg. (a) Calculate the rotational kinetic energy in the blades when they rotate at 300 rpm. (b) Calculate the translational kinetic energy of the helicopter when it flies at 20.0 m/s, and compare it with the rotational energy in the blades.

Figure \(\PageIndex{5}\): (a) Sketch of a four-blade helicopter. (b) A water rescue operation featuring a helicopter from the Auckland Westpac Rescue Helicopter Service. (credit b: modification of work by “111 Emergency”/Flickr)

Strategy

Rotational and translational kinetic energies can be calculated from their definitions. The wording of the problem gives all the necessary constants to evaluate the expressions for the rotational and translational kinetic energies.

Solution

a. The rotational kinetic energy is

\[ K = \frac{1}{2} I \omega^2 \nonumber \]

We must convert the angular velocity to radians per second and calculate the moment of inertia before we can find \(K\). The angular velocity \(\omega\) is

\[ \omega=\frac{300 \text { rev }}{1.00 \min } \frac{2 \pi \text { rad }}{1 \text { rev }} \frac{1.00 \: \min }{60.0 \: \mathrm{s}}=31.4 \: \frac{\mathrm{rad}}{\mathrm{s}}. \nonumber \]

The moment of inertia of one blade is that of a thin rod rotated about its end, listed in Figure \(\PageIndex{4}\). The total \(I\) is four times this moment of inertia because there are four blades. Thus,

\[ I=4 \frac{M l^{2}}{3}=4 \times \frac{(50.0 \: \mathrm{kg})(4.00 \: \mathrm{m})^{2}}{3}=1067.0 \: \mathrm{kg} \cdot \mathrm{m}^{2} \nonumber .\]

Entering \(\omega\) and \(I\) into the expression for rotational kinetic energy gives

\[ K=0.5\left(1067 \: \mathrm{kg} \cdot \mathrm{m}^{2}\right)(31.4 \: \mathrm{rad} / \mathrm{s})^{2}=5.26 \times 10^{5} \: \mathrm{J}. \nonumber \]

b. Entering the given values into the equation for translational kinetic energy, we obtain

\[ K=\frac{1}{2} m v^{2}=(0.5)(1000.0 \: \mathrm{kg})(20.0 \: \mathrm{m} / \mathrm{s})^{2}=2.00 \times 10^{5} \: \mathrm{J} . \nonumber \]

To compare kinetic energies, we take the ratio of translational kinetic energy to rotational kinetic energy. This ratio is

\[ \frac{2.00 \times 10^{5} \: \mathrm{J}}{5.26 \times 10^{5} \: \mathrm{J}}=0.380 . \nonumber \]

Significance

The ratio of translational energy to rotational kinetic energy is only 0.380. This ratio tells us that most of the kinetic energy of the helicopter is in its spinning blades.

Example \(\PageIndex{3}\): Energy in a boomerang

A person hurls a boomerang into the air with a velocity of 30.0 m/s at an angle of 40.0° with respect to the horizontal (Figure \(\PageIndex{6}\)). It has a mass of 1.0 kg and is rotating at 10.0 rev/s. The moment of inertia of the boomerang is given as \(I=\frac{1}{12} m L^{2} \) where \(L\) = 0.7 m. (a) What is the total energy of the boomerang when it leaves the hand? (b) How high does the boomerang go from the elevation of the hand, neglecting air resistance?

Figure \(\PageIndex{6}\): A boomerang is hurled into the air at an initial angle of 40°.

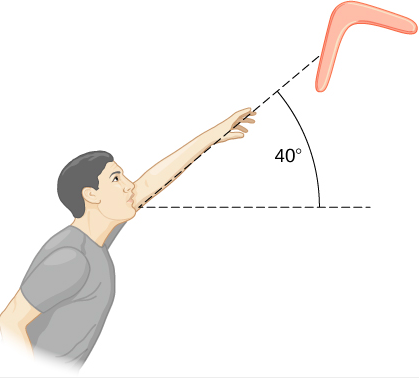
Strategy

We use the definitions of rotational and linear kinetic energy to find the total energy of the system. The problem states to neglect air resistance, so we don’t have to worry about energy loss. In part (b), we use conservation of mechanical energy to find the maximum height of the boomerang.

Solution

a. Moment of inertia: \( I=\frac{1}{12} m L^{2}=\frac{1}{12}(1.0 \: \mathrm{kg})(0.7 \: \mathrm{m})^{2}=0.041 \: \mathrm{kg} \cdot \mathrm{m}^{2}. \)

Angular Velocity: \( \omega=(10.0 \: \mathrm{rev} / \mathrm{s})(2 \pi)=62.83 \: \mathrm{rad} / \mathrm{s} \)

The rotational kinetic energy is therefore

\[ K_{R}=\frac{1}{2}\left(0.041 \: \mathrm{kg} \cdot \mathrm{m}^{2}\right)(62.83 \: \mathrm{rad} / \mathrm{s})^{2}=80.93 \: \mathrm{J} \nonumber \]

The translational kinetic energy is

\[ K_{\mathrm{T}}=\frac{1}{2} m v^{2}=\frac{1}{2}(1.0 \: \mathrm{kg})(30.0 \: \mathrm{m} / \mathrm{s})^{2}=450.0 \: \mathrm{J} \nonumber \]

Thus, the total energy in the boomerang is

\[ K_{\text {Total }}=K_{R}+K_{T}=80.93+450.0=530.93 \: \mathrm{J}. \nonumber \]

b. We use conservation of mechanical energy. Since the boomerang is launched at an angle, we need to write the total energies of the system in terms of its linear kinetic energies using the velocity in the x- and y-directions. The total energy when the boomerang leaves the hand is

\[ E_{\text {Before }}=\frac{1}{2} m v_{x}^{2}+\frac{1}{2} m v_{y}^{2}+\frac{1}{2} I \omega^{2} \nonumber \]

The total energy at maximum height is

\[ E_{\text {Final }}=\frac{1}{2} m v_{x}^{2}+\frac{1}{2} I \omega^{2}+m g h \nonumber \]

By conservation of mechanical energy, \(E_{Before} = E_{Final}\) so we have, after canceling like terms,

\[ \frac{1}{2} m v_{y}^{2}=m g h \nonumber .\]

Since \(v_y\) = 30.0 m/s (\(\sin 40^{\circ}\)) = 19.28 m/s, we find

\[ h=\frac{(19.28 \: \mathrm{m} / \mathrm{s})^{2}}{2\left(9.8 \: \mathrm{m} / \mathrm{s}^{2}\right)}=18.97 \: \mathrm{m} \nonumber \]

Significance

In part (b), the solution demonstrates how energy conservation is an alternative method to solve a problem that normally would be solved using kinematics. In the absence of air resistance, the rotational kinetic energy was not a factor in the solution for the maximum height.

Exercise 10.4

A nuclear submarine propeller has a moment of inertia of 800.0 kg • m². If the submerged propeller has a rotation rate of 4.0 rev/s when the engine is cut, what is the rotation rate of the propeller after 5.0 s when water resistance has taken 50,000 J out of the system?

More about Kinetic Energy

In this section, we show how to define the rotational kinetic energy of an object that is rotating about a stationary axis in an inertial frame of reference. Consider a solid object that is rotating about an axis with angular velocity, \(\vec\omega\), as depicted in Figure \(\PageIndex{1}\).

Figure \(\PageIndex{1}\): An object rotating about an axis that is perpendicular to the page.

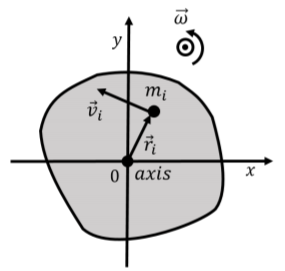
We can model the object as being composed of many point particles, each with a mass \(m_i\), located at a position \(\vec r_i\), with velocity \(\vec v_i\) relative to the axis of rotation. We choose a coordinate system whose origin is on the axis of rotation and whose \(z\) axis is co-linear with the axis of rotation, as depicted in Figure \(\PageIndex{1}\).

Each particle of mass \(m_i\) in the object has a kinetic energy, \(K_i\): \[\begin{aligned} K_i = \frac{1}{2}m_iv_i^2\end{aligned}\] We can sum the kinetic energy of each particle together to get the total rotational kinetic energy, \(K_{rot}\), of the object: \[\begin{aligned} K_{rot} = \sum_i \frac{1}{2}m_iv_i^2\end{aligned}\] Although each particle will have a different velocity, \(\vec v_i\), they will all have the same angular velocity, \(\vec\omega\). For any particle, located a distance \(r_i\) from the axis of rotation, their velocity is related to the angular velocity of the object by: \[\begin{aligned} \vec v_i &= \vec \omega \times \vec r_i\\ v_i &= \omega r_i\end{aligned}\] where \(\vec \omega\) and \(\vec r_i\) are always perpendicular to each other, since \(\vec\omega\) is out of the plane of the page. Furthermore, the velocity vector, \(\vec v_i\), will always be perpendicular to \(\vec r_i\), since all particles are moving in circles centerd about the axis of rotation. We can thus write the total rotational kinetic energy of the object using the angular speed: \[\begin{aligned} K_{rot} &= \sum_i \frac{1}{2}m_iv_i^2 = \sum_i \frac{1}{2}m_ir_i^2\omega^2= \frac{1}{2} \omega^2 \sum_i m_ir_i^2\\ &=\frac{1}{2}I\omega^2\end{aligned}\] where we factored \(\omega\) and the one half out of the sum, as these are the same for each particle \(i\). We then recognized that the remaining sum is simply the definition of the object’s moment of inertia about the axis: \[\begin{aligned} I = \sum_i mr_i^2\end{aligned}\]

Thus, the rotational kinetic energy of an object rotating with angular speed \(\omega\) about an axis that is stationary in an inertial frame of reference is given by:

\[K_{rot} = \frac{1}{2}I\omega ^{2}\]

where \(I\) is the object’s moment of inertia about that axis. The rotational kinetic energy is functionally very similar to the linear kinetic energy; instead of mass, we use the moment of inertia, and instead of speed squared, we use angular speed squared.

Work on a rotating object

We can calculate the work done by a force exerted on an object rotating about a stationary axis in an inertial frame of reference. Let \(\vec F\) be a force exerted at position, \(\vec r\), relative to the axis of rotation at some instant in time, and let the force be exerted in the plane perpendicular to the axis of rotation, as illustrated in Figure \(\PageIndex{2}\). Because the object is rotating about the given axis, only the component of the force that is tangent to the circle about which the point where the force is exerted can do work (only the component of the force that is parallel to the displacement can do work).

The work done by the force as the object rotates by a certain angle is given by: \[\begin{aligned} W = \int \vec F \cdot d\vec l = \int F_\perp dl\end{aligned}\] where \(d\vec l\) is a small displacement along the (circular) path followed by the point where the force is exerted, as illustrated in Figure \(\PageIndex{2}\). \(F_\perp\) is the component of \(\vec F\) that is perpendicular to the vector, \(\vec r\), from the axis of rotation to the location where the force is exerted (\(F_\perp\) is the component of \(\vec F\) that is tangent to the circle).

Figure \(\PageIndex{2}\): Calculating the work done by a force on a rotating object.

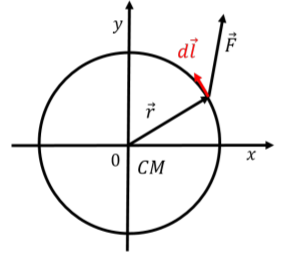
At some instant in time, when the force is exerted at position, \(\vec r\), consider the scalar product between the torque from the force, \(\vec \tau\), and an infinitesimal angular displacement, \(d\vec \theta\), about the axis of rotation: \[\begin{aligned} \vec\tau \cdot d\vec\theta = (\vec r \times \vec F) \cdot \left(\frac{1}{r^2} \vec r\times d\vec l\right)\end{aligned}\] The vectors \(\vec \tau\) and \(d\vec \theta\) are parallel to the axis of rotation (because \(\vec F\) and \(d\vec l\) are in the plane perpendicular to the axis of rotation), so their scalar product will be equal to the product of their magnitudes. The vector \(\vec r \times \vec F\) has a magnitude of: \[\begin{aligned} \vec r \times \vec F = rF_\perp\end{aligned}\] where \(F_\perp\) is the component of the force tangent to the circle. The vector \(\vec r\times d\vec l\) has a magnitude: \[\begin{aligned} \vec r\times d\vec l = rdl\end{aligned}\] since \(\vec r\) and \(d\vec l\) are always perpendicular. The scalar product \(\vec\tau \cdot d\vec\theta\) is thus equal to: \[\begin{aligned} \vec\tau \cdot d\vec\theta = rF_\perp \frac{1}{r^2} rdl = F_\perp dl\end{aligned}\] The work done by a force when an object rotates about an axis can thus be written in terms of its torque about that axis and the corresponding angular displacement from \(\theta_1\) to \(\theta_2\):

\[W=\int_{\theta _{1}}^{\theta _{2}}\vec\tau\cdot f\vec\theta \]

The net work done on an object through an angular displacement from \(\theta_1\) to \(\theta_2\) can thus be written using the net torque \(\vec \tau^{net}\) exerted on the object: \[\begin{aligned} W^{net} = \int_{\theta_1}^{\theta_2}\vec\tau^{net}\cdot d\vec \theta\end{aligned}\] We can re-arrange this using Newton’s Second Law for rotational dynamics: \[\begin{aligned} \vec\tau^{net} &= I \vec\alpha\\ &= I \frac{d\vec\omega}{dt} = I \frac{d\omega}{d\theta}\frac{d\vec\theta}{dt}=I \frac{d\omega}{d\theta} \vec\omega\end{aligned}\] which allows us to write the integral over a change in angular velocity instead of angular displacement: \[\begin{aligned} W^{net} &= \int_{\theta_1}^{\theta_2}\vec\tau^{net}\cdot d\vec \theta = \int_{\theta_1}^{\theta_2}I \frac{d\omega}{d\theta} \vec\omega \cdot d\vec \theta\\ &=\int_{\omega_1}^{\omega_2}I \omega d\omega = \frac{1}{2}I\omega_2^2 - \frac{1}{2}I\omega_1^2\end{aligned}\] where we used the fact that \(\vec\omega\) are \(d\vec\theta\) are parallel. We thus find that the Work-Energy Theorem can also be applied to find the change in rotational kinetic energy resulting from the net work done by a torque:

\[W^{net} = \int_{\theta _{1}}^{\theta _{2}}\vec\tau ^{net}\cdot d\vec\theta = \Delta K_{rot}\]

If a constant torque, \(\vec\tau\), is exerted on an object that is rotating at constant angular velocity, \(\vec\omega\), then the rate at which that work is being done is given by: \[\begin{aligned} P = \frac{dW}{dt} = \frac{d}{dt} \vec \tau \cdot d\vec\theta = \vec \tau \cdot \frac{d\vec\theta}{dt} = \vec \tau \cdot \vec\omega\end{aligned}\] This is very similar to the power, \(P=\vec F\cdot \vec v\), with which a force does work on an object moving with constant velocity, except that instead of force we use torque, and instead of velocity, we use angular velocity.

Total kinetic energy of an object

In the frame of reference of the center of mass, an object rotating about an axis through its center of mass with angular velocity, \(\vec \omega\), will have rotational kinetic energy, \(K_{rot}\), given by: \[\begin{aligned} K_{rot}=\frac{1}{2}I_{CM}\omega^2\end{aligned}\] where \(I_{CM}\) is the moment of inertia of the object about the axis through its center of mass.

We wish to determine the kinetic energy of the object in an inertial frame of reference where the object’s center of mass is moving with a velocity \(\vec v_{cm}\); that is, in a frame where the axis of rotation is moving with the velocity of the center of mass. We model the object as being composed of particles of mass, \(m_i\), each located at position, \(\vec r_i\), relative to the axis of rotation through the center of mass. The velocity, \(\vec v_i\), of a particle \(i\), in this frame of reference, is given by: \[\begin{aligned} \vec v_i = \vec\omega \times \vec r_i + \vec v_{CM}\end{aligned}\] where \(\vec\omega \times \vec r_i\) is the velocity of the particle as seen in the center of mass (due to rotation). The kinetic energy of particle \(i\), \(K_i\), is given by: \[\begin{aligned} K_i = \frac{1}{2}m_iv_i^2 = \frac{1}{2}m_i(\vec v_i\cdot \vec v_i)\end{aligned}\] where we expressed the speed of the particle squared using a scalar product of the velocity of the particle with itself. The total kinetic energy of the object is found by summing the kinetic energies of all of the particles: \[\begin{aligned} K_{tot} &= \sum \frac{1}{2}m_i(\vec v_i\cdot \vec v_i) \\ &=\frac{1}{2} \sum_i m_i (\vec\omega \times \vec r_i + \vec v_{CM}) \cdot (\vec\omega \times \vec r_i + \vec v_{CM})\\ &=\frac{1}{2} \sum_i m_i (\vec\omega \times \vec r_i)\cdot(\vec\omega \times \vec r_i ) + \frac{1}{2} \sum_i m_i (\vec v_{CM}) \cdot (\vec v_{CM}) + \sum_i m_i (\vec\omega \times \vec r_i) \cdot (\vec v_{CM})\\ &=\frac{1}{2} \sum_i m_i \omega^2r_i^2 + \frac{1}{2} \sum_i m_i v_{CM}^2 + \sum_i m_i (\vec\omega \times \vec r_i) \cdot (\vec v_{CM})\\ &=\frac{1}{2} I_{CM}\omega ^2 + \frac{1}{2}M v_{CM}^2+\sum_i m_i (\vec\omega \times \vec r_i) \cdot (\vec v_{CM})\end{aligned}\] where the first term is the rotational kinetic energy that we found earlier. The second term, called the “translational kinetic energy”, can be thought of as the kinetic energy of the whole system with mass \(M=\sum m_i\), due to the translational motion of the center of mass. The last term is identically zero; we can re-order the scalar product and factor \(\vec v_{CM}\) out of the sum: \[\begin{aligned} \sum_i m_i (\vec\omega \times \vec r_i) \cdot (\vec v_{CM}) &= (\vec v_{CM}) \cdot \sum_i m_i (\vec\omega \times \vec r_i)\\ &=(\vec v_{CM}) \cdot \sum_i m_i \vec v'_{i}\end{aligned}\] where \(v'_{i} = \vec\omega \times \vec r_i\) is the velocity of particle \(i\) in the center of mass frame of reference. But the sum: \[\begin{aligned} \sum_i m_i \vec v'_{i}\end{aligned}\] is the numerator for the definition of the velocity of the center of mass, which, in the center of mass frame of reference is identically zero!

Thus, the total kinetic energy of an object of mass, \(M\), that is rotating about an axis through its center of mass with angular velocity, \(\omega\), and whose center of mass is moving with velocity, \(\vec v_{CM}\), is given by:

\[K_{tot}=K_{rot}+K_{trans}=\frac{1}{2}I_{CM}\omega ^{2}+\frac{1}{2}Mv^{2}_{CM}\]

The total kinetic energy can be thought of as the sum of the rotational and kinetic energies.