1.2: The Seasons
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
By the end of this section, you will be able to:
- Describe how the tilt of Earth’s axis causes the seasons
- Explain how seasonal differences on Earth vary with latitude
One of the fundamental facts of life at Earth’s mid-latitudes, where most of this book’s readers live, is that there are significant variations in the heat we receive from the Sun during the course of the year. We thus divide the year into seasons, each with its different amount of sunlight. The difference between seasons gets more pronounced the farther north or south from the equator we travel, and the seasons in the Southern Hemisphere are the opposite of what we find on the northern half of Earth. With these observed facts in mind, let us ask what causes the seasons.
Many people have believed that the seasons were the result of the changing distance between Earth and the Sun. This sounds reasonable at first: it should be colder when Earth is farther from the Sun. But the facts don’t bear out this hypothesis. Although Earth’s orbit around the Sun is an ellipse, its distance from the Sun varies by only about 3%. That’s not enough to cause significant variations in the Sun’s heating. To make matters worse for people in North America who hold this hypothesis, Earth is actually closest to the Sun in January, when the Northern Hemisphere is in the middle of winter. And if distance were the governing factor, why would the two hemispheres have opposite seasons? As we shall show, the seasons are actually caused by the 23.5° tilt of Earth’s axis.
The Seasons and Sunshine
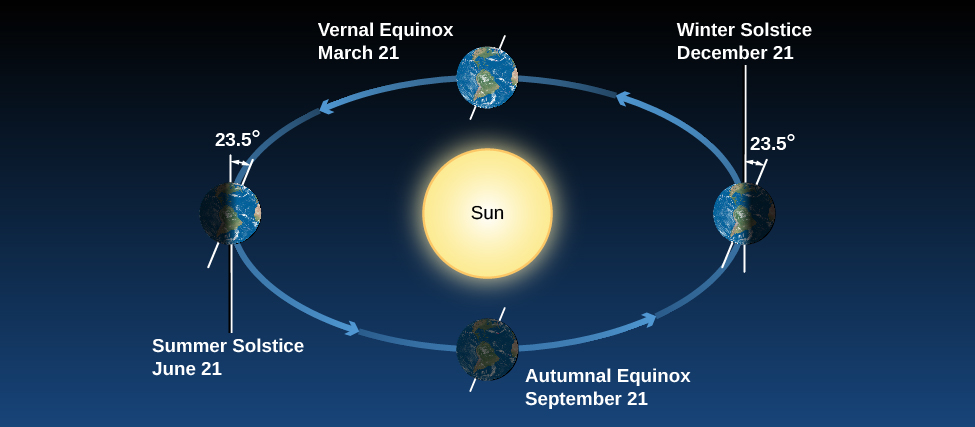
Figure 1.2.1 shows Earth’s annual path around the Sun, with Earth’s axis tilted by 23.5°. Note that our axis continues to point the same direction in the sky throughout the year. As Earth travels around the Sun, in June the Northern Hemisphere “leans into” the Sun and is more directly illuminated. In December, the situation is reversed: the Southern Hemisphere leans into the Sun, and the Northern Hemisphere leans away. In September and March, Earth leans “sideways”—neither into the Sun nor away from it—so the two hemispheres are equally favored with sunshine.
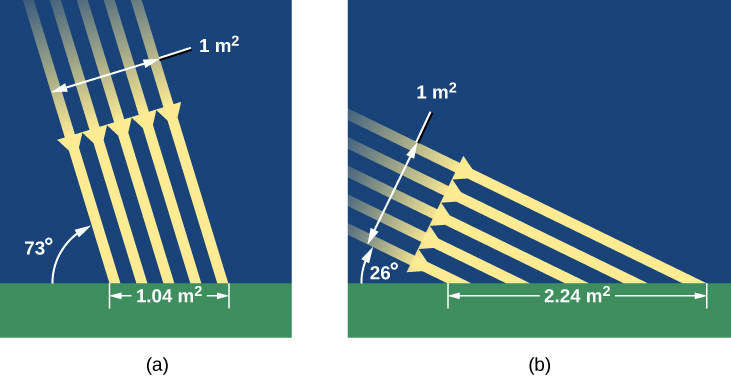
How does the Sun’s favoring one hemisphere translate into making it warmer for us down on the surface of Earth? There are two effects we need to consider. When we lean into the Sun, sunlight hits us at a more direct angle and is more effective at heating Earth’s surface (Figure 1.2.2). You can get a similar effect by shining a flashlight onto a wall. If you shine the flashlight straight on, you get an intense spot of light on the wall. But if you hold the flashlight at an angle (if the wall “leans out” of the beam), then the spot of light is more spread out. Like the straight-on light, the sunlight in June is more direct and intense in the Northern Hemisphere, and hence more effective at heating.
The second effect has to do with the length of time the Sun spends above the horizon (Figure 1.2.3). Even if you’ve never thought about astronomy before, we’re sure you have observed that the hours of daylight increase in summer and decrease in winter. Let’s see why this happens.
An equivalent way to look at our path around the Sun each year is to pretend that the Sun moves around Earth (on a circle called the ecliptic). Because Earth’s axis is tilted, the ecliptic is tilted by about 23.5° relative to the celestial equator (review Figure 2.1.6). As a result, where we see the Sun in the sky changes as the year wears on.
In June, the Sun is north of the celestial equator and spends more time with those who live in the Northern Hemisphere. It rises high in the sky and is above the horizon in the United States for as long as 15 hours. Thus, the Sun not only heats us with more direct rays, but it also has more time to do it each day. (Notice in Figure 1.2.3 that the Northern Hemisphere’s gain is the Southern Hemisphere’s loss. There the June Sun is low in the sky, meaning fewer daylight hours. In Chile, for example, June is a colder, darker time of year.) In December, when the Sun is south of the celestial equator, the situation is reversed.
Let’s look at what the Sun’s illumination on Earth looks like at some specific dates of the year, when these effects are at their maximum. On or about June 21 (the date we who live in the Northern Hemisphere call the summer solstice or sometimes the first day of summer), the Sun shines down most directly upon the Northern Hemisphere of Earth. It appears about 23° north of the equator, and thus, on that date, it passes through the zenith of places on Earth that are at 23° N latitude. The situation is shown in detail in Figure 1.2.4. To a person at 23° N (near Hawaii, for example), the Sun is directly overhead at noon. This latitude, where the Sun can appear at the zenith at noon on the first day of summer, is called the Tropic of Cancer.
We also see in Figure 1.2.4 that the Sun’s rays shine down all around the North Pole at the solstice. As Earth turns on its axis, the North Pole is continuously illuminated by the Sun; all places within 23° of the pole have sunshine for 24 hours. The Sun is as far north on this date as it can get; thus, 90° – 23° (or 67° N) is the southernmost latitude where the Sun can be seen for a full 24-hour period (sometimes called the “land of the midnight Sun”). That circle of latitude is called the Arctic Circle.
Many early cultures scheduled special events around the summer solstice to celebrate the longest days and thank their gods for making the weather warm. This required people to keep track of the lengths of the days and the northward trek of the Sun in order to know the right day for the “party.” (You can do the same thing by watching for several weeks, from the same observation point, where the Sun rises or sets relative to a fixed landmark. In spring, the Sun will rise farther and farther north of east, and set farther and farther north of west, reaching the maximum around the summer solstice.)
Now look at the South Pole in Figure 1.2.4. On June 21, all places within 23° of the South Pole—that is, south of what we call the Antarctic Circle—do not see the Sun at all for 24 hours.
The situation is reversed 6 months later, about December 21 (the date of the winter solstice, or the first day of winter in the Northern Hemisphere), as shown in Figure 1.2.5. Now it is the Arctic Circle that has the 24-hour night and the Antarctic Circle that has the midnight Sun. At latitude 23° S, called the Tropic of Capricorn, the Sun passes through the zenith at noon. Days are longer in the Southern Hemisphere and shorter in the north. In the United States and Southern Europe, there may be only 9 or 10 hours of sunshine during the day. It is winter in the Northern Hemisphere and summer in the Southern Hemisphere.
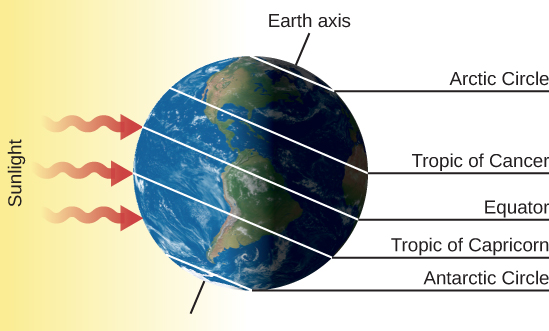
Figure 1.2.5 Earth on December 21. This is the date of the winter solstice in the Northern Hemisphere. Now the North Pole is in darkness for 24 hours and the South Pole is illuminated. The Sun is at the zenith for observers on the Tropic of Capricorn and thus is low in the sky for the residents of the Northern Hemisphere.
Example 1.2.1: Seasonal Variations
As you can see in Figure 1.2.4, the Tropic of Cancer is the latitude for which the Sun is directly overhead on the summer solstice. At this time, the Sun is at a declination of 23° N of the celestial equator, and the corresponding latitude on Earth is 23° N of the equator. If Earth were tilted a bit less, then the Tropic of Cancer would be at a lower latitude, closer to the equator.
The Arctic Circle marks the southernmost latitude for which the day length is 24 hours on the day of the summer solstice. This is located at 90° – 23° = 67° N of Earth’s equator. If Earth were tilted a bit less, then the Arctic Circle would move farther North. In the limit at which Earth is not tilted at all (its axis is perpendicular to the ecliptic), the Tropic of Cancer would be right on Earth’s equator, and the Arctic Circle would simply be the North Pole. Suppose the tilt of Earth’s axis were tilted only 5°. What would be the effect on the seasons and the locations of the Tropic of Cancer and Arctic Circle?
- Answer
-
If Earth were tilted less, the seasons would be less extreme. The variation in day length and direct sunlight would be very small over the course of a year, and the Sun’s daily path in the sky would not vary much. If Earth were tilted by 5°, the Sun’s position on the day of the summer solstice would be 5° N of the celestial equator, so the Tropic of Cancer would be at the corresponding latitude on Earth of 5° N of the Equator. The Arctic Circle would be located at 90° – 5° = 85° N of the equator.
Exercise 1.2.1
Suppose the tilt of Earth’s axis were 16°. What, then, would be the difference in latitude between the Arctic Circle and the Tropic of Cancer? What would be the effect on the seasons compared with that produced by the actual tilt of 23°?
- Answer
-
The Tropic of Cancer is at a latitude equal to Earth’s tilt, so in this case, it would be at 16° N latitude. The Arctic Circle is at a latitude equal to 90° minus Earth’s tilt, or 90° – 16° = 74°. The difference between these two latitudes is 74° – 16° = 58°. Since the tilt of Earth is less, there would be less variation in the tilt of Earth and less variation in the Sun’s paths throughout the year, so there would be milder seasonal changes.
You can see an animation of the Sun’s path during the seasons alongside a time-lapse view of light and shadow from a camera set up on the University of Nebraska campus.
Many cultures that developed some distance north of the equator have a celebration around December 21 to help people deal with the depressing lack of sunlight and the often dangerously cold temperatures. Originally, this was often a time for huddling with family and friends, for sharing the reserves of food and drink, and for rituals asking the gods to return the light and heat and turn the cycle of the seasons around. Many cultures constructed elaborate devices for anticipating when the shortest day of the year was coming. Stonehenge in England, built long before the invention of writing, is probably one such device. In our own time, we continue the winter solstice tradition with various holiday celebrations around that December date.
Halfway between the solstices, on about March 21 and September 21, the Sun is on the celestial equator. From Earth, it appears above our planet’s equator and favors neither hemisphere. Every place on Earth then receives roughly 12 hours of sunshine and 12 hours of night. The points where the Sun crosses the celestial equator are called the vernal (spring) and autumnal (fall) equinoxes.
The Seasons at Different Latitudes
The seasonal effects are different at different latitudes on Earth. Near the equator, for instance, all seasons are much the same. Every day of the year, the Sun is up half the time, so there are approximately 12 hours of sunshine and 12 hours of night. Local residents define the seasons by the amount of rain (wet season and dry season) rather than by the amount of sunlight. As we travel north or south, the seasons become more pronounced, until we reach extreme cases in the Arctic and Antarctic.
At the North Pole, all celestial objects that are north of the celestial equator are always above the horizon and, as Earth turns, circle around parallel to it. The Sun is north of the celestial equator from about March 21 to September 21, so at the North Pole, the Sun rises when it reaches the vernal equinox and sets when it reaches the autumnal equinox. Each year there are 6 months of sunshine at each pole, followed by 6 months of darkness.
Example 1.2.2: The Position of the Sun in the Sky
The Sun’s coordinates on the celestial sphere range from a declination of 23° N of the celestial equator (or +23°) to a declination 23° S of the celestial equator (or –23°). So, the Sun’s altitude at noon, when it crosses the meridian, varies by a total of 46°. What is the altitude of the Sun at noon on March 21, as seen from a place on Earth’s equator? What is its altitude on June 21, as seen from a place on Earth’s equator?
- Answer
-
On Earth’s equator, the celestial equator passes through the zenith. On March 21, the Sun is crossing the celestial equator, so it should be found at the zenith (90°) at noon. On June 21, the Sun is 23° N of the celestial equator, so it will be 23° away from the zenith at noon. The altitude above the horizon will be 23° less than the altitude of the zenith (90°), so it is 90° – 23° = 67° above the horizon.
Exercise 1.2.2
What is the altitude of the Sun at noon on December 21, as seen from a place on the Tropic of Cancer?
- Answer
-
On the day of the winter solstice, the Sun is located about 23° S of the celestial equator. From the Tropic of Cancer, a latitude of 23° N, the zenith would be a declination of 23° N. The difference in declination between zenith and the position of the Sun is 46°, so the Sun would be 46° away from the zenith. That means it would be at an altitude of 90° – 46° = 44°.
Clarifications about the Real World
In our discussions so far, we have been describing the rising and setting of the Sun and stars as they would appear if Earth had little or no atmosphere. In reality, however, the atmosphere has the curious effect of allowing us to see a little way “over the horizon.” This effect is a result of refraction, the bending of light passing through air or water, something we will discuss in Astronomical Instruments. Because of this atmospheric refraction (and the fact that the Sun is not a point of light but a disk), the Sun appears to rise earlier and to set later than it would if no atmosphere were present.
In addition, the atmosphere scatters light and provides some twilight illumination even when the Sun is below the horizon. Astronomers define morning twilight as beginning when the Sun is 18° below the horizon, and evening twilight extends until the Sun sinks more than 18° below the horizon.
These atmospheric effects require small corrections in many of our statements about the seasons. At the equinoxes, for example, the Sun appears to be above the horizon for a few minutes longer than 12 hours, and below the horizon for fewer than 12 hours. These effects are most dramatic at Earth’s poles, where the Sun actually can be seen more than a week before it reaches the celestial equator.
You probably know that the summer solstice (June 21) is not the warmest day of the year, even if it is the longest. The hottest months in the Northern Hemisphere are July and August. This is because our weather involves the air and water covering Earth’s surface, and these large reservoirs do not heat up instantaneously. You have probably observed this effect for yourself; for example, a pond does not get warm the moment the
Sun rises but is warmest late in the afternoon, after it has had time to absorb the Sun’s heat. In the same way, Earth gets warmer after it has had a chance to absorb the extra sunlight that is the Sun’s summer gift to us. And the coldest times of winter are a month or more after the winter solstice.
Key Concepts and Summary
The familiar cycle of the seasons results from the 23.5° tilt of Earth’s axis of rotation. At the summer solstice, the Sun is higher in the sky and its rays strike Earth more directly. The Sun is in the sky for more than half of the day and can heat Earth longer. At the winter solstice, the Sun is low in the sky and its rays come in at more of an angle; in addition, it is up for fewer than 12 hours, so those rays have less time to heat. At the vernal and autumnal equinoxes, the Sun is on the celestial equator and we get about 12 hours of day and night. The seasons are different at different latitudes.
Footnotes
1Note that the dates indicated for the solstices and equinoxes are approximate; depending on the year, they may occur a day or two earlier or later.
Contributors and Attributions
Andrew Fraknoi (Foothill College), David Morrison (NASA Ames Research Center), Sidney C. Wolff (National Optical Astronomy Observatory) with many contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/astronomy).


