5.2: Planets beyond the Solar System- Search and Discovery
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
By the end of this section, you will be able to:
- Describe the orbital motion of planets in our solar system using Kepler’s laws
- Compare the indirect and direct observational techniques for exoplanet detection
For centuries, astronomers have dreamed of finding planets around other stars, including other planets like Earth. Direct observations of such distant planets are very difficult, however. You might compare a planet orbiting a star to a mosquito flying around one of those giant spotlights at a shopping center opening. From close up, you might spot the mosquito. But imagine viewing the scene from some distance away—say, from an airplane. You could see the spotlight just fine, but what are your chances of catching the mosquito in that light? Instead of making direct images, astronomers have relied on indirect observations and have now succeeded in detecting a multitude of planets around other stars.
In 1995, after decades of effort, we found the first such exoplanet (a planet outside our solar system) orbiting a main-sequence star, and today we know that most stars form with planets. This is an example of how persistence and new methods of observation advance the knowledge of humanity. By studying exoplanets, astronomers hope to better understand our solar system in context of the rest of the universe. For instance, how does the arrangement of our solar system compare to planetary systems in the rest of the universe? What do exoplanets tell us about the process of planet formation? And how does knowing the frequency of exoplanets influence our estimates of whether there is life elsewhere?
Searching for Orbital Motion
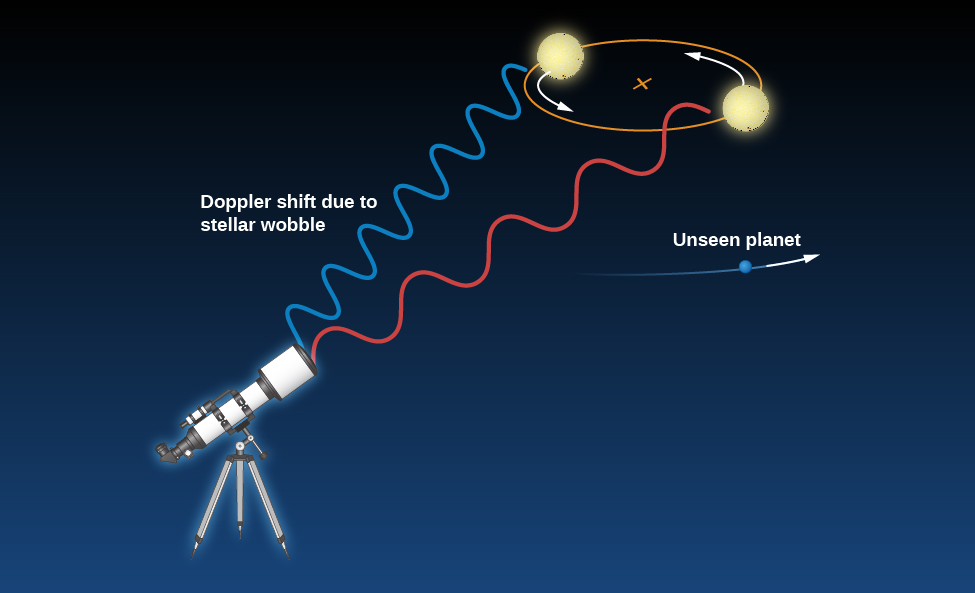
Most exoplanet detections are made using techniques where we observe the effect that the planet exerts on the host star. For example, the gravitational tug of an unseen planet will cause a small wobble in the host star. Or, if its orbit is properly aligned, a planet will periodically cross in front of the star, causing the brightness of the star to dim.
To understand how a planet can move its host star, consider a single Jupiter-like planet. Both the planet and the star actually revolve about their common center of mass. Remember that gravity is a mutual attraction. The star and the planet each exert a force on the other, and we can find a stable point, the center of mass, between them about which both objects move. The smaller the mass of a body in such a system, the larger its orbit. A massive star barely swings around the center of mass, while a low-mass planet makes a much larger “tour.”
Suppose the planet is like Jupiter and has a mass about one-thousandth that of its star; in this case, the size of the star’s orbit is one-thousandth the size of the planet’s. To get a sense of how difficult observing such motion might be, let’s see how hard Jupiter would be to detect in this way from the distance of a nearby star. Consider an alien astronomer trying to observe our own system from Alpha Centauri, the closest star system to our own (about 4.3 light-years away). There are two ways this astronomer could try to detect the orbital motion of the Sun. One way would be to look for changes in the Sun’s position on the sky. The second would be to use the Doppler effect to look for changes in its velocity. Let’s discuss each of these in turn.
The diameter of Jupiter’s apparent orbit viewed from Alpha Centauri is 10 seconds of arc, and that of the Sun’s orbit is 0.010 seconds of arc. (Remember, 1 second of arc is 1/3600 degree.) If they could measure the apparent position of the Sun (which is bright and easy to detect) to sufficient precision, they would describe an orbit of diameter 0.010 seconds of arc with a period equal to that of Jupiter, which is 12 years.
In other words, if they watched the Sun for 12 years, they would see it wiggle back and forth in the sky by this minuscule fraction of a degree. From the observed motion and the period of the “wiggle,” they could deduce the mass of Jupiter and its distance using Kepler’s laws. (To refresh your memory about these laws, see Chapter 2 on Orbits and Gravity.)
Measuring positions in the sky this accurately is extremely difficult, and so far, astronomers have not made any confirmed detections of planets using this technique. However, we have been successful in using spectrometers to measure the changing velocity of stars with planets around them.
As the star and planet orbit each other, part of their motion will be in our line of sight (toward us or away from us). Such motion can be measured using the Doppler effect and the star’s spectrum. As the star moves back and forth in orbit around the system’s center of mass in response to the gravitational tug of an orbiting planet, the lines in its spectrum will shift back and forth.
Let’s again consider the example of the Sun. Its radial velocity (motion toward or away from us) changes by about 13 meters per second with a period of 12 years because of the gravitational pull of Jupiter. This corresponds to about 30 miles per hour, roughly the speed at which many of us drive around town. Detecting motion at this level in a star’s spectrum presents an enormous technical challenge, but several groups of astronomers around the world, using specialized spectrographs designed for this purpose, have succeeded. Note that the change in speed does not depend on the distance of the star from the observer. Using the Doppler effect to detect planets will work at any distance, as long as the star is bright enough to provide a good spectrum and a large telescope is available to make the observations (Figure 5.2.1).
The first successful use of the Doppler effect to find a planet around another star was in 1995. Michel Mayor and Didier Queloz of the Geneva Observatory (Figure 5.2.2) used this technique to find a planet orbiting a star resembling our Sun called 51 Pegasi, about 40 light-years away. (The star can be found in the sky near the great square of Pegasus, the flying horse of Greek mythology, one of the easiest-to-find star patterns.) To everyone’s surprise, the planet takes a mere 4.2 days to orbit around the star. (Remember that Mercury, the innermost planet in our solar system, takes 88 days to go once around the Sun, so 4.2 days seems fantastically short.)

Mayor and Queloz’s findings mean the planet must be very close to 51 Pegasi, circling it about 7 million kilometers away (Figure 5.2.3). At that distance, the energy of the star should heat the planet’s surface to a temperature of a few thousand degrees Celsius (a bit hot for future tourism). From its motion, astronomers calculate that it has at least half the mass of Jupiter1, making it clearly a jovian and not a terrestrial-type planet.

Since that initial planet discovery, the rate of progress has been breathtaking. Hundreds of giant planets have been discovered using the Doppler technique. Many of these giant planets are orbiting close to their stars—astronomers have called these hot Jupiters.
The existence of giant planets so close to their stars was a surprise, and these discoveries have forced us to rethink our ideas about how planetary systems form. But for now, bear in mind that the Doppler-shift method—which relies on the pull of a planet making its star “wiggle” back and forth around the center of mass—is most effective at finding planets that are both close to their stars and massive. These planets cause the biggest “wiggles” in the motion of their stars and the biggest Doppler shifts in the spectrum. Plus, they will be found sooner, since astronomers like to monitor the star for at least one full orbit (and perhaps more) and hot Jupiters take the shortest time to complete their orbit.
So if such planets exist, we would expect to be finding this type first. Scientists call this a selection effect—where our technique of discovery selects certain kinds of objects as “easy finds.” As an example of a selection effect in everyday life, imagine you decide you are ready for a new romantic relationship in your life. To begin with, you only attend social events on campus, all of which require a student ID to get in. Your selection of possible partners will then be limited to students at your college. That may not give you as diverse a group to choose from as you want. In the same way, when we first used the Doppler technique, it selected massive planets close to their stars as the most likely discoveries. As we spend longer times watching target stars and as our ability to measure smaller Doppler shifts improves, this technique can reveal more distant and less massive planets too.
View a series of animations demonstrating solar system motion, Kepler’s laws, and exoplanet radial velocity planet detection.
Transiting Planets
The second method for indirect detection of exoplanets is based not on the motion of the star but on its brightness. When the orbital plane of the planet is tilted or inclined so that it is viewed edge-on, we will see the planet cross in front of the star once per orbit, causing the star to dim slightly; this event is known as transit. Figure 5.2.4 shows a sketch of the transit at three time steps: (1) out of transit, (2) the start of transit, and (3) full transit, along with a sketch of the light curve, which shows the drop in the brightness of the host star. The amount of light blocked—the depth of the transit—depends on the area of the planet (its size) compared to the star. If we can determine the size of the star, the transit method tells us the size of the planet.
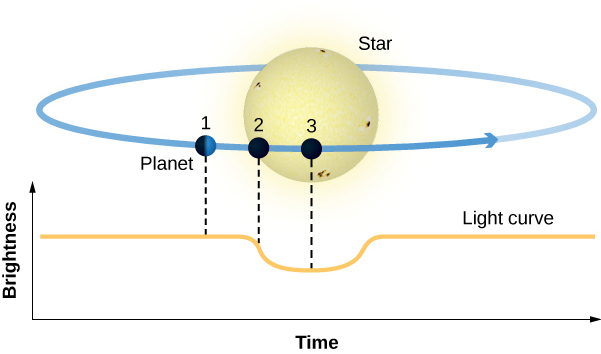
The interval between successive transits is the length of the year for that planet, which can be used (again using Kepler’s laws) to find its distance from the star. Larger planets like Jupiter block out more starlight than small earthlike planets, making transits by giant planets easier to detect, even from ground-based observatories. But by going into space, above the distorting effects of Earth’s atmosphere, the transit technique has been extended to exoplanets as small as Mars.
Example 5.2.1: Transit Depth
In a transit, the planet’s circular disk blocks the light of the star’s circular disk. The area of a circle is πR2. The amount of light the planet blocks, called the transit depth, is then given by
πR2planetπR2star=R2planetR2star=(RplanetRstar)2
Now calculate the transit depth for a star the size of the Sun with a gas giant planet the size of Jupiter.
- Answer
-
The radius of Jupiter is 71,400 km, while the radius of the Sun is 695,700 km. Substituting into the equation, we get
(RplanetRstar)2=(71,400 km695,700 km)2=0.01
or 1%, which can easily be detected with the instruments on board the Kepler spacecraft.
Exercise 5.2.1
What is the transit depth for a star half the size of the Sun with a much smaller planet, like the size of Earth?
- Answer
-
The radius of Earth is 6371 km. Therefore,
(RplanetRstar)2=(6371 km695,700/2 km)2=(6371 km347,850 km)2=0.0003
or significantly less than 1%.
The Doppler method allows us to estimate the mass of a planet. If the same object can be studied by both the Doppler and transit techniques, we can measure both the mass and the size of the exoplanet. This is a powerful combination that can be used to derive the average density (mass/volume) of the planet. In 1999, using measurements from ground-based telescopes, the first transiting planet was detected orbiting the star HD 209458. The planet transits its parent star for about 3 hours every 3.5 days as we view it from Earth. Doppler measurements showed that the planet around HD 209458 has about 70% the mass of Jupiter, but its radius is about 35% larger than Jupiter’s. This was the first case where we could determine what an exoplanet was made of—with that mass and radius, HD 209458 must be a gas and liquid world like Jupiter or Saturn.
It is even possible to learn something about the planet’s atmosphere. When the planet passes in front of HD 209458, the atoms in the planet’s atmosphere absorb starlight. Observations of this absorption were first made at the wavelengths of yellow sodium lines and showed that the atmosphere of the planet contains sodium; now, other elements can be measured as well.
Try a transit simulator that demonstrates how a planet passing in front of its parent star can lead to the planet’s detection. Follow the instructions to run the animation on your computer.
Transiting planets reveal such a wealth of information that the French Space Agency (CNES) and the European Space Agency (ESA) launched the CoRoT space telescope in 2007 to detect transiting exoplanets. CoRoT discovered 32 transiting exoplanets, including the first transiting planet with a size and density similar to Earth. In 2012, the spacecraft suffered an onboard computer failure, ending the mission. Meanwhile, NASA built a much more powerful transit observatory called Kepler.
In 2009, NASA launched the Kepler space telescope, dedicated to the discovery of transiting exoplanets. This spacecraft stared continuously at more than 150,000 stars in a small patch of sky near the constellation of Cygnus—just above the plane of our Milky Way Galaxy (Figure 5.2.5). Kepler’s cameras and ability to measure small changes in brightness very precisely enabled the discovery of thousands of exoplanets, including many multi-planet systems. The spacecraft required three reaction wheels—a type of wheel used to help control slight rotation of the spacecraft—to stabilize the pointing of the telescope and monitor the brightness of the same group of stars over and over again. Kepler was launched with four reaction wheels (one a spare), but by May 2013, two wheels had failed and the telescope could no longer be accurately pointed toward the target area. Kepler had been designed to operate for 4 years, and ironically, the pointing failure occurred exactly 4 years and 1 day after it began observing.
However, this failure did not end the mission. The Kepler telescope continued to observe for two more years, looking for short-period transits in different parts of the sky. A new NASA mission called TESS (Transiting Exoplanet Survey Satellite) is now carrying out a transit survey all over the sky of the nearer (and therefore brighter) stars.

What do we mean, exactly, by “discovery” of transiting exoplanets? A single transit shows up as a very slight drop in the brightness of the star, lasting several hours. However, astronomers must be on guard against other factors that might produce a false transit, especially when working at the limit of precision of the telescope. We must wait for a second transit of similar depth. But when another transit is observed, we don’t initially know whether it might be due to another planet in a different orbit. The “discovery” occurs only when a third transit is found with similar depth and the same spacing in time as the first pair.
Computers normally conduct the analysis, which involves searching for tiny, periodic dips in the light from each star, extending over 4 years of observation. But the Kepler mission also has a program in which non-astronomers—citizen scientists—can examine the data. These dedicated volunteers have found several transits that were missed by the computer analyses, showing that the human eye and brain sometimes recognize unusual events that a computer was not programmed to look for.
Measuring three or four evenly spaced transits is normally enough to “discover” an exoplanet. But in a new field like exoplanet research, we would like to find further independent verification. The strongest confirmation happens when ground-based telescopes are also able to detect a Doppler shift with the same period as the transits. However, this is generally not possible for Earth-size planets. One of the most convincing ways to verify that a dip in brightness is due to a planet is to find more planets orbiting the same star—a planetary system. Multi-planet systems also provide alternative ways to estimate the masses of the planets, as we will discuss in the next section.
The selection effects (or biases) in the Kepler data are similar to those in Doppler observations. Large planets are easier to find than small ones, and short-period planets are easier than long-period planets. If we require three transits to establish the presence of a planet, we are of course limited to discovering planets with orbital periods less than one-third of the observing interval. Thus, it was only in its fourth and final year of operation that Kepler was able to find planets with orbits like Earth’s that require 1 year to go around their star.
Direct Detection
The best possible evidence for an earthlike planet elsewhere would be an image. After all, “seeing is believing” is a very human prejudice. But imaging a distant planet is a formidable challenge indeed. Suppose, for example, you were a great distance away and wished to detect reflected light from Earth. Earth intercepts and reflects less than one billionth of the Sun’s radiation, so its apparent brightness in visible light is less than one billionth that of the Sun. Compounding the challenge of detecting such a faint speck of light, the planet is swamped by the blaze of radiation from its parent star.
Even today, the best telescope mirrors’ optics have slight imperfections that prevent the star’s light from coming into focus in a completely sharp point.
Direct imaging works best for young gas giant planets that emit infrared light and reside at large separations from their host stars. Young giant planets emit more infrared light because they have more internal energy, stored from the process of planet formation. Even then, clever techniques must be employed to subtract out the light from the host star. In 2008, three such young planets were discovered orbiting HR 8799, a star in the constellation of Pegasus (Figure 5.2.6:). Two years later, a fourth planet was detected closer to the star. Additional planets may reside even closer to HR 8799, but if they exist, they are currently lost in the glare of the star.
Since then, a number of planets around other stars have been found using direct imaging. However, one challenge is to tell whether the objects we are seeing are indeed planets or if they are brown dwarfs (failed stars) in orbit around a star.

Direct imaging is an important technique for characterizing an exoplanet. The brightness of the planet can be measured at different wavelengths. These observations provide an estimate for the temperature of the planet’s atmosphere; in the case of HR 8799 planet 1, the color suggests the presence of thick clouds. Spectra can also be obtained from the faint light to analyze the atmospheric constituents. A spectrum of HR 8799 planet 1 indicates a hydrogen-rich atmosphere, while the closer planet 4 shows evidence for methane in the atmosphere.
Another way to overcome the blurring effect of Earth’s atmosphere is to observe from space. Infrared may be the optimal wavelength range in which to observe because planets get brighter in the infrared while stars like our Sun get fainter, thereby making it easier to detect a planet against the glare of its star. Special optical techniques can be used to suppress the light from the central star and make it easier to see the planet itself. However, even if we go into space, it will be difficult to obtain images of Earth-size planets.
Key Concepts and Summary
Several observational techniques have successfully detected planets orbiting other stars. These techniques fall into two general categories—direct and indirect detection. The Doppler and transit techniques are our most powerful indirect tools for finding exoplanets. Some planets are also being found by direct imaging.
Footnotes
1The Doppler method only allows us to find the minimum mass of a planet. To determine the exact mass using the Doppler shift and Kepler’s laws, we must also have the angle at which the planet’s orbit is oriented to our view—something we don’t have any independent way of knowing in most cases. Still, if the minimum mass is half of Jupiter’s, the actual mass can only be larger than that, and we are sure that we are dealing with a jovian planet.
Glossary
- exoplanet
- a planet orbiting a star other than our Sun
- transit
- when one astronomical object moves in front of another
Contributors and Attributions
Andrew Fraknoi (Foothill College), David Morrison (NASA Ames Research Center), Sidney C. Wolff (National Optical Astronomy Observatory) with many contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/astronomy).


