12.2: Evolution of Massive Stars- An Explosive Finish
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
By the end of this section, you will be able to:
- Describe the interior of a massive star before a supernova
- Explain the steps of a core collapse and explosion
- List the hazards associated with nearby supernovae
Thanks to mass loss, then, stars with starting masses up to at least 8 MSun (and perhaps even more) probably end their lives as white dwarfs. But we know stars can have masses as large as 150 (or more) MSun. They have a different kind of death in store for them. As we will see, these stars die with a bang.
Nuclear Fusion of Heavy Elements
After the helium in its core is exhausted (see The Evolution of More Massive Stars), the evolution of a massive star takes a significantly different course from that of lower-mass stars. In a massive star, the weight of the outer layers is sufficient to force the carbon core to contract until it becomes hot enough to fuse carbon into oxygen, neon, and magnesium. This cycle of contraction, heating, and the ignition of another nuclear fuel repeats several more times. After each of the possible nuclear fuels is exhausted, the core contracts again until it reaches a new temperature high enough to fuse still-heavier nuclei. The products of carbon fusion can be further converted into silicon, sulfur, calcium, and argon. And these elements, when heated to a still-higher temperature, can combine to produce iron. Massive stars go through these stages very, very quickly. In really massive stars, some fusion stages toward the very end can take only months or even days! This is a far cry from the millions of years they spend in the main-sequence stage.
At this stage of its evolution, a massive star resembles an onion with an iron core. As we get farther from the center, we find shells of decreasing temperature in which nuclear reactions involve nuclei of progressively lower mass—silicon and sulfur, oxygen, neon, carbon, helium, and finally, hydrogen (Figure 12.2.1).
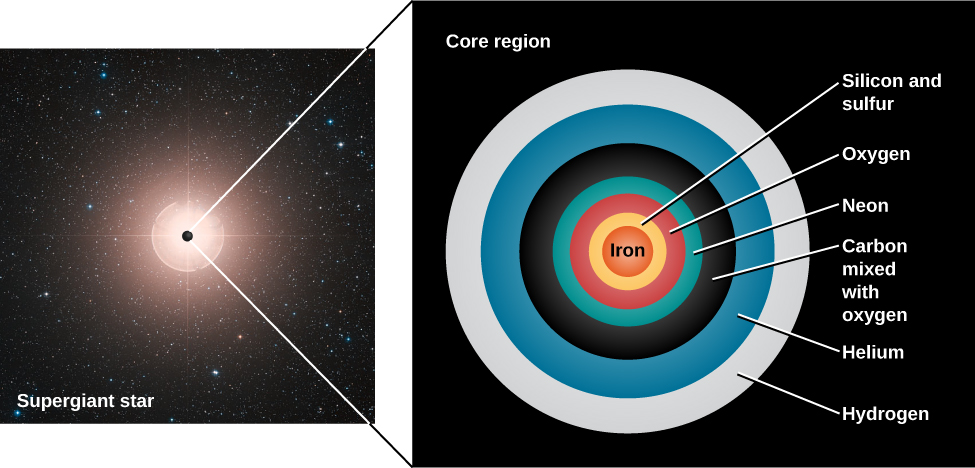
But there is a limit to how long this process of building up elements by fusion can go on. The fusion of silicon into iron turns out to be the last step in the sequence of nonexplosive element production. Up to this point, each fusion reaction has produced energy because the nucleus of each fusion product has been a bit more stable than the nuclei that formed it. As discussed in The Sun: A Nuclear Powerhouse, light nuclei give up some of their binding energy in the process of fusing into more tightly bound, heavier nuclei. It is this released energy that maintains the outward pressure in the core so that the star does not collapse. But of all the nuclei known, iron is the most tightly bound and thus the most stable.
You might think of the situation like this: all smaller nuclei want to “grow up” to be like iron, and they are willing to pay (produce energy) to move toward that goal. But iron is a mature nucleus with good self-esteem, perfectly content being iron; it requires payment (must absorb energy) to change its stable nuclear structure. This is the exact opposite of what has happened in each nuclear reaction so far: instead of providing energy to balance the inward pull of gravity, any nuclear reactions involving iron would remove some energy from the core of the star.
Unable to generate energy, the star now faces catastrophe.
Collapse into a Ball of Neutrons
When nuclear reactions stop, the core of a massive star is supported by degenerate electrons, just as a white dwarf is. For stars that begin their evolution with masses of at least 10 MSun, this core is likely made mainly of iron. (For stars with initial masses in the range 8 to 10 MSun, the core is likely made of oxygen, neon, and magnesium, because the star never gets hot enough to form elements as heavy as iron. The exact composition of the cores of stars in this mass range is very difficult to determine because of the complex physical characteristics in the cores, particularly at the very high densities and temperatures involved.) We will focus on the more massive iron cores in our discussion.
While no energy is being generated within the white dwarf core of the star, fusion still occurs in the shells that surround the core. As the shells finish their fusion reactions and stop producing energy, the ashes of the last reaction fall onto the white dwarf core, increasing its mass. As Figure 23.1.1 in Section 23.1 shows, a higher mass means a smaller core. The core can contract because even a degenerate gas is still mostly empty space. Electrons and atomic nuclei are, after all, extremely small. The electrons and nuclei in a stellar core may be crowded compared to the air in your room, but there is still lots of space between them.
The electrons at first resist being crowded closer together, and so the core shrinks only a small amount. Ultimately, however, the iron core reaches a mass so large that even degenerate electrons can no longer support it. When the density reaches 4 × 1011g/cm3 (400 billion times the density of water), some electrons are actually squeezed into the atomic nuclei, where they combine with protons to form neutrons and neutrinos. This transformation is not something that is familiar from everyday life, but becomes very important as such a massive star core collapses.
Some of the electrons are now gone, so the core can no longer resist the crushing mass of the star’s overlying layers. The core begins to shrink rapidly. More and more electrons are now pushed into the atomic nuclei, which ultimately become so saturated with neutrons that they cannot hold onto them.
At this point, the neutrons are squeezed out of the nuclei and can exert a new force. As is true for electrons, it turns out that the neutrons strongly resist being in the same place and moving in the same way. The force that can be exerted by such degenerate neutrons is much greater than that produced by degenerate electrons, so unless the core is too massive, they can ultimately stop the collapse.
This means the collapsing core can reach a stable state as a crushed ball made mainly of neutrons, which astronomers call a neutron star. We don’t have an exact number (a “Chandrasekhar limit”) for the maximum mass of a neutron star, but calculations tell us that the upper mass limit of a body made of neutrons might only be about 3 MSun. So if the mass of the core were greater than this, then even neutron degeneracy would not be able to stop the core from collapsing further. The dying star must end up as something even more extremely compressed, which until recently was believed to be only one possible type of object—the state of ultimate compaction known as a black hole (which is the subject of our next chapter). This is because no force was believed to exist that could stop a collapse beyond the neutron star stage.
Collapse and Explosion
When the collapse of a high-mass star’s core is stopped by degenerate neutrons, the core is saved from further destruction, but it turns out that the rest of the star is literally blown apart. Here’s how it happens.
The collapse that takes place when electrons are absorbed into the nuclei is very rapid. In less than a second, a core with a mass of about 1 MSun, which originally was approximately the size of Earth, collapses to a diameter of less than 20 kilometers. The speed with which material falls inward reaches one-fourth the speed of light. The collapse halts only when the density of the core exceeds the density of an atomic nucleus (which is the densest form of matter we know). A typical neutron star is so compressed that to duplicate its density, we would have to squeeze all the people in the world into a single sugar cube! This would give us one sugar cube’s worth (one cubic centimeter’s worth) of a neutron star.
The neutron degenerate core strongly resists further compression, abruptly halting the collapse. The shock of the sudden jolt initiates a shock wave that starts to propagate outward. However, this shock alone is not enough to create a star explosion. The energy produced by the outflowing matter is quickly absorbed by atomic nuclei in the dense, overlying layers of gas, where it breaks up the nuclei into individual neutrons and protons.
Our understanding of nuclear processes indicates (as we mentioned above) that each time an electron and a proton in the star’s core merge to make a neutron, the merger releases a neutrino. These ghostly subatomic particles, introduced in The Sun: A Nuclear Powerhouse, carry away some of the nuclear energy. It is their presence that launches the final disastrous explosion of the star. The total energy contained in the neutrinos is huge. In the initial second of the star’s explosion, the power carried by the neutrinos (1046 watts) is greater than the power put out by all the stars in over a billion galaxies.
While neutrinos ordinarily do not interact very much with ordinary matter (we earlier accused them of being downright antisocial), matter near the center of a collapsing star is so dense that the neutrinos do interact with it to some degree. They deposit some of this energy in the layers of the star just outside the core. This huge, sudden input of energy reverses the infall of these layers and drives them explosively outward. Most of the mass of the star (apart from that which went into the neutron star in the core) is then ejected outward into space. As we saw earlier, such an explosion requires a star of at least 8 MSun, and the neutron star can have a mass of at most 3 MSun. Consequently, at least five times the mass of our Sun is ejected into space in each such explosive event!
The resulting explosion is called a supernova (Figure 12.2.2). When these explosions happen close by, they can be among the most spectacular celestial events, as we will discuss in the next section. (Actually, there are at least two different types of supernova explosions: the kind we have been describing, which is the collapse of a massive star, is called, for historical reasons, a type II supernova. We will describe how the types differ later in this chapter).
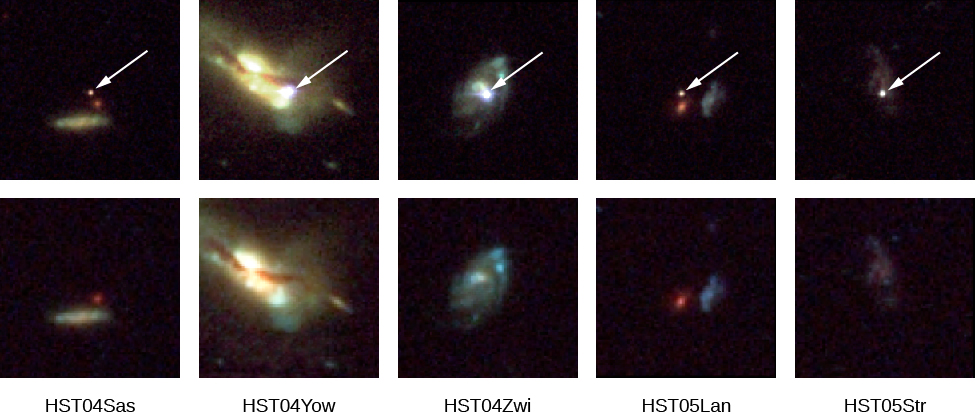
Table 12.2.1 summarizes the discussion so far about what happens to stars and substellar objects of different initial masses at the ends of their lives. Like so much of our scientific understanding, this list represents a progress report: it is the best we can do with our present models and observations. The mass limits corresponding to various outcomes may change somewhat as models are improved. There is much we do not yet understand about the details of what happens when stars die.
| Initial Mass (Mass of Sun = 1)1 | Final State at the End of Its Life |
|---|---|
| < 0.01 | Planet |
| 0.01 to 0.08 | Brown dwarf |
| 0.08 to 0.25 | White dwarf made mostly of helium |
| 0.25 to 8 | White dwarf made mostly of carbon and oxygen |
| 8 to 10 | White dwarf made of oxygen, neon, and magnesium |
| 10 to 40 | Supernova explosion that leaves a neutron star |
| > 40 | Supernova explosion that leaves a black hole |
The Supernova Giveth and the Supernova Taketh Away
After the supernova explosion, the life of a massive star comes to an end. But the death of each massive star is an important event in the history of its galaxy. The elements built up by fusion during the star’s life are now “recycled” into space by the explosion, making them available to enrich the gas and dust that form new stars and planets. Because these heavy elements ejected by supernovae are critical for the formation of planets and the origin of life, it’s fair to say that without mass loss from supernovae and planetary nebulae, neither the authors nor the readers of this book would exist.
But the supernova explosion has one more creative contribution to make, one we alluded to in Stars from Adolescence to Old Age when we asked where the atoms in your jewelry came from. The supernova explosion produces a flood of energetic neutrons that barrel through the expanding material. These neutrons can be absorbed by iron and other nuclei where they can turn into protons. Thus, they build up elements that are more massive than iron, including such terrestrial favorites as gold and silver. This is the only place we know where such heavier atoms as lead or uranium can be made. Next time you wear some gold jewelry (or give some to your sweetheart), bear in mind that those gold atoms were once part of an exploding star!
When supernovae explode, these elements (as well as the ones the star made during more stable times) are ejected into the existing gas between the stars and mixed with it. Thus, supernovae play a crucial role in enriching their galaxy with heavier elements, allowing, among other things, the chemical elements that make up earthlike planets and the building blocks of life to become more common as time goes on (Figure 12.2.3).
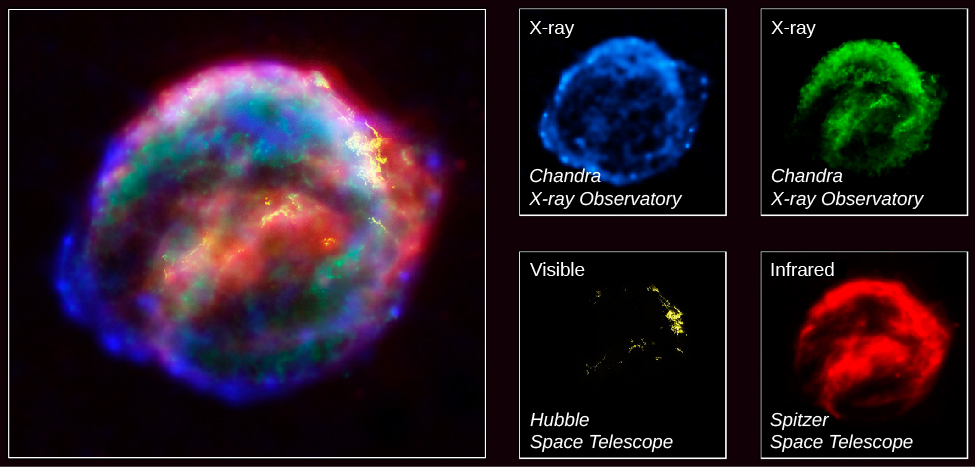
Supernovae are also thought to be the source of many of the high-energy cosmic ray particles discussed in Cosmic Rays. Trapped by the magnetic field of the Galaxy, the particles from exploded stars continue to circulate around the vast spiral of the Milky Way. Scientists speculate that high-speed cosmic rays hitting the genetic material of Earth organisms over billions of years may have contributed to the steady mutations—subtle changes in the genetic code—that drive the evolution of life on our planet. In all the ways we have mentioned, supernovae have played a part in the development of new generations of stars, planets, and life.
But supernovae also have a dark side. Suppose a life form has the misfortune to develop around a star that happens to lie near a massive star destined to become a supernova. Such life forms may find themselves snuffed out when the harsh radiation and high-energy particles from the neighboring star’s explosion reach their world. If, as some astronomers speculate, life can develop on many planets around long-lived (lower-mass) stars, then the suitability of that life’s own star and planet may not be all that matters for its long-term evolution and survival. Life may well have formed around a number of pleasantly stable stars only to be wiped out because a massive nearby star suddenly went supernova. Just as children born in a war zone may find themselves the unjust victims of their violent neighborhood, life too close to a star that goes supernova may fall prey to having been born in the wrong place at the wrong time.
What is a safe distance to be from a supernova explosion? A lot depends on the violence of the particular explosion, what type of supernova it is (see The Evolution of Binary Star Systems), and what level of destruction we are willing to accept. Calculations suggest that a supernova less than 50 light-years away from us would certainly end all life on Earth, and that even one 100 light-years away would have drastic consequences for the radiation levels here. One minor extinction of sea creatures about 2 million years ago on Earth may actually have been caused by a supernova at a distance of about 120 light-years.
The good news is that there are at present no massive stars that promise to become supernovae within 50 light-years of the Sun. (This is in part because the kinds of massive stars that become supernovae are overall quite rare.) The massive star closest to us, Spica (in the constellation of Virgo), is about 260 light-years away, probably a safe distance, even if it were to explode as a supernova in the near future.
Example 12.2.1: Extreme Gravity
In this section, you were introduced to some very dense objects. How would those objects’ gravity affect you? Recall that the force of gravity, F, between two bodies is calculated as
F=GM1M2R2
where G is the gravitational constant, 6.67×10–11 Nm2/kg2, M1 and M2 are the masses of the two bodies, and R is their separation. Also, from Newton’s second law,
F=M×a
where a is the acceleration of a body with mass M.
So let’s consider the situation of a mass—say, you—standing on a body, such as Earth or a white dwarf (where we assume you will be wearing a heat-proof space suit). You are M1 and the body you are standing on is M2. The distance between you and the center of gravity of the body on which you stand is its radius, R. The force exerted on you is
F=M1×a=GM1M2R2
Solving for a, the acceleration of gravity on that world, we get
g=(G×M)R2
Note that we have replaced the general symbol for acceleration, a, with the symbol scientists use for the acceleration of gravity, g.
Say that a particular white dwarf has the mass of the Sun (2 × 1030 kg) but the radius of Earth (6.4 × 106 m). What is the acceleration of gravity at the surface of the white dwarf?
- Answer
-
The acceleration of gravity at the surface of the white dwarf is
g (white dwarf)=(G×MSun)R2Earth=(6.67×10−11 m2/kg s2×2×1030 kg)(6.4×106 m)2=3.26×106 m/s2
Compare this to g on the surface of Earth, which is 9.8 m/s2.
Exercise 12.2.1
What is the acceleration of gravity at the surface if the white dwarf has the twice the mass of the Sun and is only half the radius of Earth?
- Answer
-
g (white dwarf)=(G×2MSun)(0.5REarth)2=(6.67×10−11 m2/kg s2×4×1030 kg)(3.2×106)2=2.61×107 m/s2
Summary
In a massive star, hydrogen fusion in the core is followed by several other fusion reactions involving heavier elements. Just before it exhausts all sources of energy, a massive star has an iron core surrounded by shells of silicon, sulfur, oxygen, neon, carbon, helium, and hydrogen. The fusion of iron requires energy (rather than releasing it). If the mass of a star’s iron core exceeds the Chandrasekhar limit (but is less than 3 MSun), the core collapses until its density exceeds that of an atomic nucleus, forming a neutron star with a typical diameter of 20 kilometers. The core rebounds and transfers energy outward, blowing off the outer layers of the star in a type II supernova explosion.
Footnotes
1Stars in the mass ranges 0.25–8 and 8–10 may later produce a type of supernova different from the one we have discussed so far. These are discussed in The Evolution of Binary Star Systems.
Glossary
- neutron star
- a compact object of extremely high density composed almost entirely of neutrons
- type II supernova
- a stellar explosion produced at the endpoint of the evolution of stars whose mass exceeds roughly 10 times the mass of the Sun
Contributors and Attributions
Andrew Fraknoi (Foothill College), David Morrison (NASA Ames Research Center), Sidney C. Wolff (National Optical Astronomy Observatory) with many contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/astronomy).


