8.17: Rocket Propulsion
- Last updated
- Jun 17, 2019
- Save as PDF
- Page ID
- 17969

- Boundless
- Boundless
( \newcommand{\kernel}{\mathrm{null}\,}\)
Rocket Propulsion, Changing Mass, and Momentum
In rocket propulsion, matter is forcefully ejected from a system, producing an equal and opposite reaction on what remains.
learning objectives
- Identify physical principles of rocket propulsion
Rocket Propulsion, Changing Mass, and Momentum
Rockets range in size from fireworks so small that ordinary people use them to immense Saturn Vs that once propelled massive payloads toward the Moon. The propulsion of all rockets, jet engines, deflating balloons, and even squids and octopuses is explained by the same physical principle: Newton’s third law of motion. Matter is forcefully ejected from a system, producing an equal and opposite reaction on what remains. Another common example is the recoil of a gun. The gun exerts a force on a bullet to accelerate it and consequently experiences an equal and opposite force, causing the gun’s recoil or kick.
shows a rocket accelerating straight up. In part (a), the rocket has a mass m and a velocity v relative to Earth, and hence a momentum mv. In part (b), a time Δt has elapsed in which the rocket has ejected a mass Δm of hot gas at a velocity ve relative to the rocket. The remainder of the mass (m−m) now has a greater velocity (v+Δv). The momentum of the entire system (rocket plus expelled gas) has actually decreased because the force of gravity has acted for a time Δt, producing a negative impulse Δp=−mgΔt. (Remember that impulse is the net external force on a system multiplied by the time it acts, and it equals the change in momentum of the system. ) So the center of mass of the system is in free fall but, by rapidly expelling mass, part of the system can accelerate upward. It is a commonly held misconception that the rocket exhaust pushes on the ground. If we consider thrust; that is, the force exerted on the rocket by the exhaust gases, then a rocket’s thrust is greater in outer space than in the atmosphere or on the launch pad. In fact, gases are easier to expel into a vacuum.
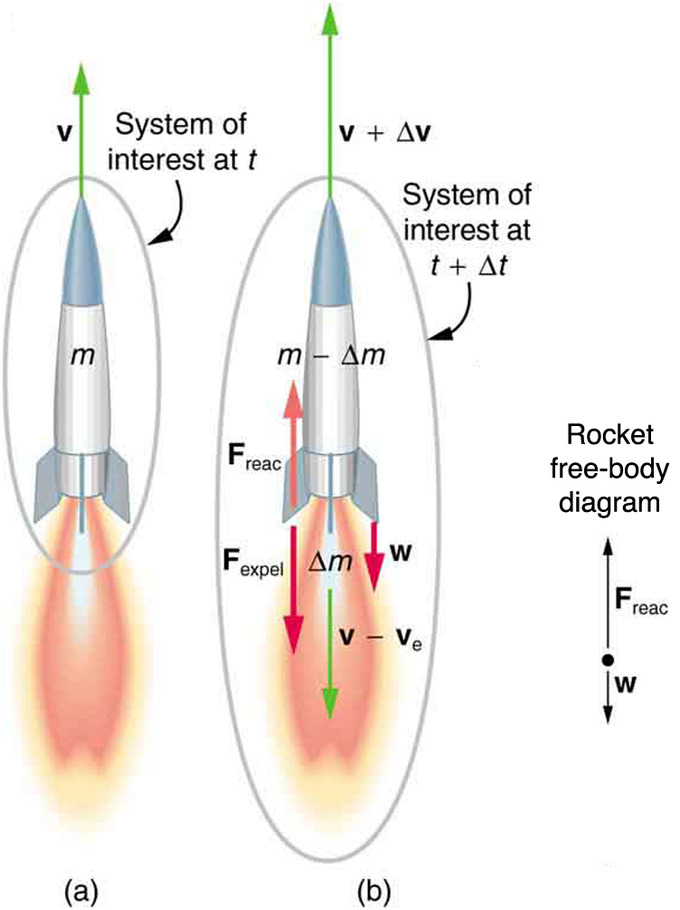
Free-body diagram of rocket propulsion: (a) This rocket has a mass m and an upward velocity v. The net external force on the system is −mg, if air resistance is neglected. (b) A time Δt later the system has two main parts, the ejected gas and the remainder of the rocket. The reaction force on the rocket is what overcomes the gravitational force and accelerates it upward.
By calculating the change in momentum for the entire system over Δt, and equating this change to the impulse, the following expression can be shown to be a good approximation for the acceleration of the rocket.
a=vemΔmΔt−g
where a is the acceleration of the rocket, ve is the escape velocity, m is the mass of the rocket, Δm is the mass of the ejected gas, and Δt is the time in which the gas is ejected.
Factors of Acceleration
A rocket’s acceleration depends on three major factors, consistent with the equation for acceleration of a rocket. First, the greater the exhaust velocity of the gases relative to the rocket, ve, the greater the acceleration is. The practical limit for ve is about 2.5×103m/s for conventional (non-nuclear) hot-gas propulsion systems. The second factor is the rate at which mass is ejected from the rocket. This is the factor ΔmΔt in the equation. The quantity (ΔmΔt)ve, with units of newtons, is called “thrust.” The faster the rocket burns its fuel, the greater its thrust, and the greater its acceleration. The third factor is the mass m of the rocket. The smaller the mass is (all other factors being the same), the greater the acceleration. The rocket mass m decreases dramatically during flight because most of the rocket is fuel to begin with, so that acceleration increases continuously, reaching a maximum just before the fuel is exhausted.
To achieve the high speeds needed to hop continents, obtain orbit, or escape Earth’s gravity altogether, the mass of the rocket other than fuel must be as small as possible. It can be shown that, in the absence of air resistance and neglecting gravity, the final velocity of a one-stage rocket initially at rest is
v=velnm0mr
where ln(m0/mr) is the natural logarithm of the ratio of the initial mass of the rocket (m0) to what is left (mr) after all of the fuel is exhausted. (Note that v is actually the change in velocity, so the equation can be used for any segment of the flight. If we start from rest, the change in velocity equals the final velocity. )
Key Points
- The propulsion of all rockets is explained by the same physical principle: Newton’s third law of motion.
- A rocket’s acceleration depends on three major factors: the exhaust velocity, the rate the exhaust is ejected, and the mass of the rocket.
- To achieve the high speeds needed to hop continents, obtain orbit, or escape Earth’s gravity altogether, the mass of the rocket other than fuel must be as small as possible.
Key Terms
- Newton’s third law of motion: states that all forces exist in pairs: if one object A exerts a force FA on a second object B, then B simultaneously exerts a force FB on A, and the two forces are equal and opposite: FA=−FB.
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
- Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- OpenStax College, Introduction to Rocket Propulsion. September 18, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42166/latest/. License: CC BY: Attribution
- Sunil Kumar Singh, Rocket. September 18, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m14866/latest/. License: CC BY: Attribution
- OpenStax College, Introduction to Rocket Propulsion. September 18, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42166/latest/. License: CC BY: Attribution
- OpenStax College, Introduction to Rocket Propulsion. September 18, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42166/latest/. License: CC BY: Attribution
- Newton's third law of motion. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Newton's%20third%20law%20of%20motion. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, Introduction to Rocket Propulsion. November 3, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42166/latest/. License: CC BY: Attribution

