Temperature and Heat (Exercises)
- Last updated
- Save as PDF
- Page ID
- 18029
Conceptual Questions
1.1: Temperature and Thermal Equilibrium
1. What does it mean to say that two systems are in thermal equilibrium?
2. Give an example in which A has some kind of non-thermal equilibrium relationship with B, and B has the same relationship with C, but A does not have that relationship with C.
1.2: Thermometers and Temperature Scales
3. If a thermometer is allowed to come to equilibrium with the air, and a glass of water is not in equilibrium with the air, what will happen to the thermometer reading when it is placed in the water?
4. Give an example of a physical property that varies with temperature and describe how it is used to measure temperature.
1.3: Thermal Expansion
5. Pouring cold water into hot glass or ceramic cookware can easily break it. What causes the breaking? Explain why Pyrex®, a glass with a small coefficient of linear expansion, is less susceptible.
6. One method of getting a tight fit, say of a metal peg in a hole in a metal block, is to manufacture the peg slightly larger than the hole. The peg is then inserted when at a different temperature than the block. Should the block be hotter or colder than the peg during insertion? Explain your answer.
7. Does it really help to run hot water over a tight metal lid on a glass jar before trying to open it? Explain your answer.
8. When a cold alcohol thermometer is placed in a hot liquid, the column of alcohol goes down slightly before going up. Explain why.
9. Calculate the length of a 1-meter rod of a material with thermal expansion coefficient αα when the temperature is raised from 300 K to 600 K. Taking your answer as the new initial length, find the length after the rod is cooled back down to 300 K. Is your answer 1 meter? Should it be? How can you account for the result you got?
10. Noting the large stresses that can be caused by thermal expansion, an amateur weapon inventor decides to use it to make a new kind of gun. He plans to jam a bullet against an aluminum rod inside a closed invar tube. When he heats the tube, the rod will expand more than the tube and a very strong force will build up. Then, by a method yet to be determined, he will open the tube in a split second and let the force of the rod launch the bullet at very high speed. What is he overlooking?
1.4: Heat Transfer, Specific Heat, and Calorimetry
11. How is heat transfer related to temperature?
12. Describe a situation in which heat transfer occurs.
13. When heat transfers into a system, is the energy stored as heat? Explain briefly.
14. The brakes in a car increase in temperature by ΔT when bringing the car to rest from a speed \(v\). How much greater would ΔT be if the car initially had twice the speed? You may assume the car stops fast enough that no heat transfers out of the brakes.
1.5: Phase Changes
15. A pressure cooker contains water and steam in equilibrium at a pressure greater than atmospheric pressure. How does this greater pressure increase cooking speed?
16. As shown below, which is the phase diagram for carbon dioxide, what is the vapor pressure of solid carbon dioxide (dry ice) at −78.5°C?−78.5°C? (Note that the axes in the figure are nonlinear and the graph is not to scale.)
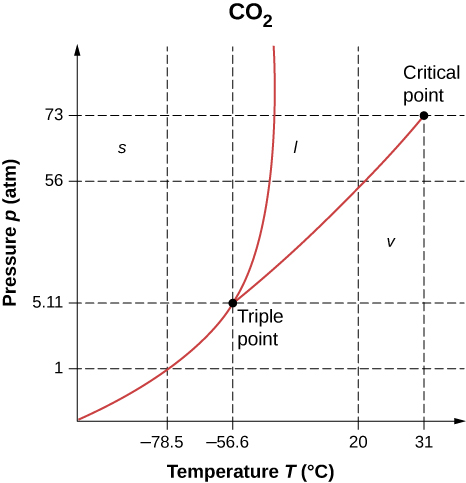
17. Can carbon dioxide be liquefied at room temperature (20°C)? If so, how? If not, why not? (See the phase diagram in the preceding problem.)
18. What is the distinction between gas and vapor?
19. Heat transfer can cause temperature and phase changes. What else can cause these changes?
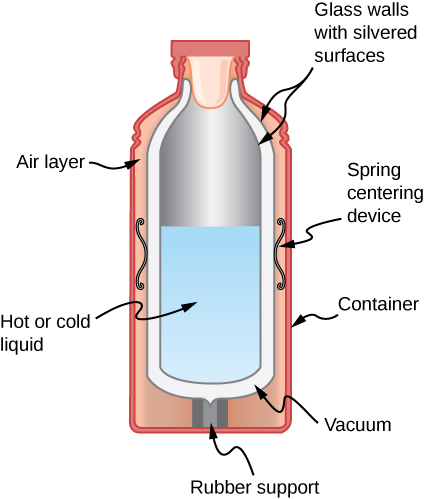
20. How does the latent heat of fusion of water help slow the decrease of air temperatures, perhaps preventing temperatures from falling significantly below 0°C, in the vicinity of large bodies of water?
21. What is the temperature of ice right after it is formed by freezing water?
22. If you place 0°C ice into 0°C water in an insulated container, what will the net result be? Will there be less ice and more liquid water, or more ice and less liquid water, or will the amounts stay the same?
23. What effect does condensation on a glass of ice water have on the rate at which the ice melts? Will the condensation speed up the melting process or slow it down?
24. In Miami, Florida, which has a very humid climate and numerous bodies of water nearby, it is unusual for temperatures to rise above about 38°C (100°F). In the desert climate of Phoenix, Arizona, however, temperatures rise above that almost every day in July and August. Explain how the evaporation of water helps limit high temperatures in humid climates.
25. In winter, it is often warmer in San Francisco than in Sacramento, 150 km inland. In summer, it is nearly always hotter in Sacramento. Explain how the bodies of water surrounding San Francisco moderate its extreme temperatures.
26. Freeze-dried foods have been dehydrated in a vacuum. During the process, the food freezes and must be heated to facilitate dehydration. Explain both how the vacuum speeds up dehydration and why the food freezes as a result.
27. In a physics classroom demonstration, an instructor inflates a balloon by mouth and then cools it in liquid nitrogen. When cold, the shrunken balloon has a small amount of light blue liquid in it, as well as some snow-like crystals. As it warms up, the liquid boils, and part of the crystals sublime, with some crystals lingering for a while and then producing a liquid. Identify the blue liquid and the two solids in the cold balloon. Justify your identifications using data from Table 1.4.
1.6: Mechanisms of Heat Transfer
28. What are the main methods of heat transfer from the hot core of Earth to its surface? From Earth’s surface to outer space?
29. When our bodies get too warm, they respond by sweating and increasing blood circulation to the surface to transfer thermal energy away from the core. What effect will those processes have on a person in a 40.0-°C hot tub?
30. Shown below is a cut-away drawing of a thermos bottle (also known as a Dewar flask), which is a device designed specifically to slow down all forms of heat transfer. Explain the functions of the various parts, such as the vacuum, the silvering of the walls, the thin-walled long glass neck, the rubber support, the air layer, and the
31. Some electric stoves have a flat ceramic surface with heating elements hidden beneath. A pot placed over a heating element will be heated, while the surface only a few centimeters away is safe to touch. Why is ceramic, with a conductivity less than that of a metal but greater than that of a good insulator, an ideal choice for the stove top?
32. Loose-fitting white clothing covering most of the body, shown below, is ideal for desert dwellers, both in the hot Sun and during cold evenings. Explain how such clothing is advantageous during both day and night.
33. One way to make a fireplace more energy-efficient is to have room air circulate around the outside of the fire box and back into the room. Detail the methods of heat transfer involved.
34. On cold, clear nights horses will sleep under the cover of large trees. How does this help them keep warm?
35. When watching a circus during the day in a large, dark-colored tent, you sense significant heat transfer from the tent. Explain why this occurs.
36. Satellites designed to observe the radiation from cold (3 K) dark space have sensors that are shaded from the Sun, Earth, and the Moon and are cooled to very low temperatures. Why must the sensors be at low temperature?
37. Why are thermometers that are used in weather stations shielded from the sunshine? What does a thermometer measure if it is shielded from the sunshine? What does it measure if it is not?
38. Putting a lid on a boiling pot greatly reduces the heat transfer necessary to keep it boiling. Explain why.
39. Your house will be empty for a while in cold weather, and you want to save energy and money. Should you turn the thermostat down to the lowest level that will protect the house from damage such as freezing pipes, or leave it at the normal temperature? (If you don’t like coming back to a cold house, imagine that a timer controls the heating system so the house will be warm when you get back.) Explain your answer.
40. You pour coffee into an unlidded cup, intending to drink it 5 minutes later. You can add cream when you pour the cup or right before you drink it. (The cream is at the same temperature either way. Assume that the cream and coffee come into thermal equilibrium with each other very quickly.) Which way will give you hotter coffee? What feature of this question is different from the previous one?
41. Broiling is a method of cooking by radiation, which produces somewhat different results from cooking by conduction or convection. A gas flame or electric heating element produces a very high temperature close to the food and above it. Why is radiation the dominant heat-transfer method in this situation?
42. On a cold winter morning, why does the metal of a bike feel colder than the wood of a porch?
Problems
1.2: Thermometers and Temperature Scales
43. While traveling outside the United States, you feel sick. A companion gets you a thermometer, which says your temperature is 39. What scale is that on? What is your Fahrenheit temperature? Should you seek medical help?
44. What are the following temperatures on the Kelvin scale?
(a) 68.0°F, an indoor temperature sometimes recommended for energy conservation in winter
(b) 134°F, one of the highest atmospheric temperatures ever recorded on Earth (Death Valley, California, 1913)
(c) 9890°F, the temperature of the surface of the Sun
45. (a) Suppose a cold front blows into your locale and drops the temperature by 40.0 Fahrenheit degrees. How many degrees Celsius does the temperature decrease when it decreases by 40.0°F? (b) Show that any change in temperature in Fahrenheit degrees is nine-fifths the change in Celsius degrees
46. An Associated Press article on climate change said, “Some of the ice shelf’s disappearance was probably during times when the planet was 36 degrees Fahrenheit (2 degrees Celsius) to 37 degrees Fahrenheit (3 degrees Celsius) warmer than it is today.” What mistake did the reporter make?
47. (a) At what temperature do the Fahrenheit and Celsius scales have the same numerical value? (b) At what temperature do the Fahrenheit and Kelvin scales have the same numerical value?
48. A person taking a reading of the temperature in a freezer in Celsius makes two mistakes: first omitting the negative sign and then thinking the temperature is Fahrenheit. That is, the person reads –x°C as x°F. Oddly enough, the result is the correct Fahrenheit temperature. What is the original Celsius reading? Round your answer to three significant figures.
1.4: Heat Transfer, Specific Heat, and Calorimetry
49. The height of the Washington Monument is measured to be 170.00 m on a day when the temperature is 35.0°C. What will its height be on a day when the temperature falls to −10.0°C? Although the monument is made of limestone, assume that its coefficient of thermal expansion is the same as that of marble. Give your answer to five significant figures.
50. How much taller does the Eiffel Tower become at the end of a day when the temperature has increased by 15°C? Its original height is 321 m and you can assume it is made of steel.
51. What is the change in length of a 3.00-cm-long column of mercury if its temperature changes from 37.0°C to 40.0°C, assuming the mercury is constrained to a cylinder but unconstrained in length? Your answer will show why thermometers contain bulbs at the bottom instead of simple columns of liquid.
52. How large an expansion gap should be left between steel railroad rails if they may reach a maximum temperature 35.0°C greater than when they were laid? Their original length is 10.0 m.
53. You are looking to buy a small piece of land in Hong Kong. The price is “only” $60,000 per square meter. The land title says the dimensions are 20m×30m. By how much would the total price change if you measured the parcel with a steel tape measure on a day when the temperature was 20°C above the temperature that the tape measure was designed for? The dimensions of the land do not change.
54. Global warming will produce rising sea levels partly due to melting ice caps and partly due to the expansion of water as average ocean temperatures rise. To get some idea of the size of this effect, calculate the change in length of a column of water 1.00 km high for a temperature increase of 1.00°C. Assume the column is not free to expand sideways. As a model of the ocean, that is a reasonable approximation, as only parts of the ocean very close to the surface can expand sideways onto land, and only to a limited degree. As another approximation, neglect the fact that ocean warming is not uniform with depth.
55. (a) Suppose a meter stick made of steel and one made of aluminum are the same length at 0°C. What is their difference in length at 22.0°C?
(b) Repeat the calculation for two 30.0-m-long surveyor’s tapes.
56. (a) If a 500-mL glass beaker is filled to the brim with ethyl alcohol at a temperature of 5.00°C, how much will overflow when the alcohol’s temperature reaches the room temperature of 22.0°C?
(b) How much less water would overflow under the same conditions?
57. Most cars have a coolant reservoir to catch radiator fluid that may overflow when the engine is hot. A radiator is made of copper and is filled to its 16.0-L capacity when at 10.0°C. What volume of radiator fluid will overflow when the radiator and fluid reach a temperature of 95.0°C, given that the fluid’s volume coefficient of expansion is β=400×10−6/°C? (Your answer will be a conservative estimate, as most car radiators have operating temperatures greater than 95.0°C).
58. A physicist makes a cup of instant coffee and notices that, as the coffee cools, its level drops 3.00 mm in the glass cup. Show that this decrease cannot be due to thermal contraction by calculating the decrease in level if the \(350cm^3\) of coffee is in a 7.00-cm-diameter cup and decreases in temperature from 95.0°C to 45.0°C. (Most of the drop in level is actually due to escaping bubbles of air.)
59. The density of water at 0°C is very nearly \(1000kg/m^3\) (it is actually \(999.84kg/m^3\)), whereas the density of ice at 0°C0°C is \(917kg/m^3\). Calculate the pressure necessary to keep ice from expanding when it freezes, neglecting the effect such a large pressure would have on the freezing temperature. (This problem gives you only an indication of how large the forces associated with freezing water might be.)
60. Show that β=3α, by calculating the infinitesimal change in volume dV of a cube with sides of length L when the temperature changes by dT.
1.4: Thermal Expansion
61. On a hot day, the temperature of an 80,000-L swimming pool increases by 1.50°C. What is the net heat transfer during this heating? Ignore any complications, such as loss of water by evaporation.
62. To sterilize a 50.0-g glass baby bottle, we must raise its temperature from 22.0°C to 95.0°C. How much heat transfer is required?
63. The same heat transfer into identical masses of different substances produces different temperature changes. Calculate the final temperature when 1.00 kcal of heat transfers into 1.00 kg of the following, originally at 20.0°C:
(a) water;
(b) concrete;
(c) steel; and
(d) mercury.
64. Rubbing your hands together warms them by converting work into thermal energy. If a woman rubs her hands back and forth for a total of 20 rubs, at a distance of 7.50 cm per rub, and with an average frictional force of 40.0 N, what is the temperature increase? The mass of tissues warmed is only 0.100 kg, mostly in the palms and fingers.
65. A 0.250-kg block of a pure material is heated from 20.0°C to 65.0°C by the addition of 4.35 kJ of energy. Calculate its specific heat and identify the substance of which it is most likely composed.
66. Suppose identical amounts of heat transfer into different masses of copper and water, causing identical changes in temperature. What is the ratio of the mass of copper to water?
67. (a) The number of kilocalories in food is determined by calorimetry techniques in which the food is burned and the amount of heat transfer is measured. How many kilocalories per gram are there in a 5.00-g peanut if the energy from burning it is transferred to 0.500 kg of water held in a 0.100-kg aluminum cup, causing a 54.9-°Ctemperature increase? Assume the process takes place in an ideal calorimeter, in other words a perfectly insulated container.
(b) Compare your answer to the following labeling information found on a package of dry roasted peanuts: a serving of 33 g contains 200 calories. Comment on whether the values are consistent.
68. Following vigorous exercise, the body temperature of an 80.0 kg person is 40.0°C. At what rate in watts must the person transfer thermal energy to reduce the body temperature to 37.0°C in 30.0 min, assuming the body continues to produce energy at the rate of 150 W? (1watt=1joule/secondor1W=1J/s)
69. In a study of healthy young \(men^1\), doing 20 push-ups in 1 minute burned an amount of energy per kg that for a 70.0-kg man corresponds to 8.06 calories (kcal). How much would a 70.0-kg man’s temperature rise if he did not lose any heat during that time?
70. A 1.28-kg sample of water at 10.0°C is in a calorimeter. You drop a piece of steel with a mass of 0.385 kg at 215°C into it. After the sizzling subsides, what is the final equilibrium temperature? (Make the reasonable assumptions that any steam produced condenses into liquid water during the process of equilibration and that the evaporation and condensation don’t affect the outcome, as we’ll see in the next section.)
71. Repeat the preceding problem, assuming the water is in a glass beaker with a mass of 0.200 kg, which in turn is in a calorimeter. The beaker is initially at the same temperature as the water. Before doing the problem, should the answer be higher or lower than the preceding answer? Comparing the mass and specific heat of the beaker to those of the water, do you think the beaker will make much difference?
1.5: Phase Changes
72. How much heat transfer (in kilocalories) is required to thaw a 0.450-kg package of frozen vegetables originally at 0°C if their heat of fusion is the same as that of water?
73. A bag containing 0°C ice is much more effective in absorbing energy than one containing the same amount of 0°C water.
(a) How much heat transfer is necessary to raise the temperature of 0.800 kg of water from 0°C to 30.0°C?
(b) How much heat transfer is required to first melt 0.800 kg of 0°C ice and then raise its temperature?
(c) Explain how your answer supports the contention that the ice is more effective.
74. (a) How much heat transfer is required to raise the temperature of a 0.750-kg aluminum pot containing 2.50 kg of water from 30.0°C to the boiling point and then boil away 0.750 kg of water?
(b) How long does this take if the rate of heat transfer is 500 W?
75. Condensation on a glass of ice water causes the ice to melt faster than it would otherwise. If 8.00 g of vapor condense on a glass containing both water and 200 g of ice, how many grams of the ice will melt as a result? Assume no other heat transfer occurs. Use (L_v\) for water at 37°C as a better approximation than \(L_v\) for water at 100°C.)
76. On a trip, you notice that a 3.50-kg bag of ice lasts an average of one day in your cooler. What is the average power in watts entering the ice if it starts at 0°C and completely melts to 0°C water in exactly one day?
77. On a certain dry sunny day, a swimming pool’s temperature would rise by 1.50°C if not for evaporation. What fraction of the water must evaporate to carry away precisely enough energy to keep the temperature constant?
78. (a) How much heat transfer is necessary to raise the temperature of a 0.200-kg piece of ice from −20.0°C to130.0°C, including the energy needed for phase changes?
(b) How much time is required for each stage, assuming a constant 20.0 kJ/s rate of heat transfer? (c) Make a graph of temperature versus time for this process.
79. In 1986, an enormous iceberg broke away from the Ross Ice Shelf in Antarctica. It was an approximately rectangular prism 160 km long, 40.0 km wide, and 250 m thick.
(a) What is the mass of this iceberg, given that the density of ice is \(917kg/m^3\)?
(b) How much heat transfer (in joules) is needed to melt it?
(c) How many years would it take sunlight alone to melt ice this thick, if the ice absorbs an average of \(100W/m^2\), 12.00 h per day?
80. How many grams of coffee must evaporate from 350 g of coffee in a 100-g glass cup to cool the coffee and the cup from 95.0°C to 45.0°C? Assume the coffee has the same thermal properties as water and that the average heat of vaporization is 2340 kJ/kg (560 kcal/g). Neglect heat losses through processes other than evaporation, as well as the change in mass of the coffee as it cools. Do the latter two assumptions cause your answer to be higher or lower than the true answer?
81. (a) It is difficult to extinguish a fire on a crude oil tanker, because each liter of crude oil releases \(2.80×10^7J\) of energy when burned. To illustrate this difficulty, calculate the number of liters of water that must be expended to absorb the energy released by burning 1.00 L of crude oil, if the water’s temperature rises from 20.0°C to 100°C, it boils, and the resulting steam’s temperature rises to 300°C at constant pressure.
(b) Discuss additional complications caused by the fact that crude oil is less dense than water.
82. The energy released from condensation in thunderstorms can be very large. Calculate the energy released into the atmosphere for a small storm of radius 1 km, assuming that 1.0 cm of rain is precipitated uniformly over this area.
83. To help prevent frost damage, 4.00 kg of water at 0°Cis sprayed onto a fruit tree.
(a) How much heat transfer occurs as the water freezes?
(b) How much would the temperature of the 200-kg tree decrease if this amount of heat transferred from the tree? Take the specific heat to be 3.35kJ/kg⋅°C, and assume that no phase change occurs in the tree.
84. A 0.250-kg aluminum bowl holding 0.800kg of soup at 25.0°C is placed in a freezer. What is the final temperature if 388 kJ of energy is transferred from the bowl and soup, assuming the soup’s thermal properties are the same as that of water?
85. A 0.0500-kg ice cube at −30.0°C is placed in 0.400 kg of 35.0-°C water in a very well-insulated container. What is the final temperature?
86. If you pour 0.0100 kg of 20.0°C water onto a 1.20-kg block of ice (which is initially at −15.0°C), what is the final temperature? You may assume that the water cools so rapidly that effects of the surroundings are negligible.
87. Indigenous people sometimes cook in watertight baskets by placing hot rocks into water to bring it to a boil. What mass of 500-°C granite must be placed in 4.00 kg of 15.0-°C water to bring its temperature to 100°C, if 0.0250 kg of water escapes as vapor from the initial sizzle? You may neglect the effects of the surroundings.
88. What would the final temperature of the pan and water be in Example 1.7 if 0.260 kg of water were placed in the pan and 0.0100 kg of the water evaporated immediately, leaving the remainder to come to a common temperature with the pan?
1.6: Mechanisms of Heat Transfer
89. (a) Calculate the rate of heat conduction through house walls that are 13.0 cm thick and have an average thermal conductivity twice that of glass wool. Assume there are no windows or doors. The walls’ surface area is \(120m^2\) and their inside surface is at 18.0°C, while their outside surface is at 5.00°C.
(b) How many 1-kW room heaters would be needed to balance the heat transfer due to conduction?
90. The rate of heat conduction out of a window on a winter day is rapid enough to chill the air next to it. To see just how rapidly the windows transfer heat by conduction, calculate the rate of conduction in watts through a \(3.00-m^2\)window that is 0.634 cm thick (1/4 in.) if the temperatures of the inner and outer surfaces are 5.00°C and −10.0°C−, respectively. (This rapid rate will not be maintained—the inner surface will cool, even to the point of frost formation.)
91. Calculate the rate of heat conduction out of the human body, assuming that the core internal temperature is 37.0°C, the skin temperature is 34.0°C, the thickness of the fatty tissues between the core and the skin averages 1.00 cm, and the surface area is \(1.40m^2\).
92. Suppose you stand with one foot on ceramic flooring and one foot on a wool carpet, making contact over an area of \(80.0cm^2\) with each foot. Both the ceramic and the carpet are 2.00 cm thick and are 10.0°C on their bottom sides. At what rate must heat transfer occur from each foot to keep the top of the ceramic and carpet at 33.0°C?
93. A man consumes 3000 kcal of food in one day, converting most of it to thermal energy to maintain body temperature. If he loses half this energy by evaporating water (through breathing and sweating), how many kilograms of water evaporate?
94. A firewalker runs across a bed of hot coals without sustaining burns. Calculate the heat transferred by conduction into the sole of one foot of a firewalker given that the bottom of the foot is a 3.00-mm-thick callus with a conductivity at the low end of the range for wood and its density is \(300kg/m^3\). The area of contact is \(25.0cm^2\), the temperature of the coals is 700°C, and the time in contact is 1.00 s. Ignore the evaporative cooling of sweat.
95. (a) What is the rate of heat conduction through the 3.00-cm-thick fur of a large animal having a \(1.40-m^2\) surface area? Assume that the animal’s skin temperature is 32.0°C, that the air temperature is −5.00°C, and that fur has the same thermal conductivity as air.
(b) What food intake will the animal need in one day to replace this heat transfer?
96. A walrus transfers energy by conduction through its blubber at the rate of 150 W when immersed in −1.00°C water. The walrus’s internal core temperature is 37.0°C, and it has a surface area of \(2.00m^2\). What is the average thickness of its blubber, which has the conductivity of fatty tissues without blood?
97. Compare the rate of heat conduction through a 13.0-cm-thick wall that has an area of \(10.0m^2\) and a thermal conductivity twice that of glass wool with the rate of heat conduction through a 0.750-cm-thick window that has an area of \(2.00m^2\), assuming the same temperature difference across each.
98. Suppose a person is covered head to foot by wool clothing with average thickness of 2.00 cm and is transferring energy by conduction through the clothing at the rate of 50.0 W. What is the temperature difference across the clothing, given the surface area is \(1.40m^2\)?
99. Some stove tops are smooth ceramic for easy cleaning. If the ceramic is 0.600 cm thick and heat conduction occurs through the same area and at the same rate as computed in Example 1.11, what is the temperature difference across it? Ceramic has the same thermal conductivity as glass and brick.
100. One easy way to reduce heating (and cooling) costs is to add extra insulation in the attic of a house. Suppose a single-story cubical house already had 15 cm of fiberglass insulation in the attic and in all the exterior surfaces. If you added an extra 8.0 cm of fiberglass to the attic, by what percentage would the heating cost of the house drop? Take the house to have dimensions 10 m by 15 m by 3.0 m. Ignore air infiltration and heat loss through windows and doors, and assume that the interior is uniformly at one temperature and the exterior is uniformly at another.
101. Many decisions are made on the basis of the payback period: the time it will take through savings to equal the capital cost of an investment. Acceptable payback times depend upon the business or philosophy one has. (For some industries, a payback period is as small as 2 years.) Suppose you wish to install the extra insulation in the preceding problem. If energy cost $1.00 per million joules and the insulation was $4.00 per square meter, then calculate the simple payback time. Take the average ΔT for the 120-day heating season to be 15.0°C.
Additional Problems
102. In 1701, the Danish astronomer Ole Rømer proposed a temperature scale with two fixed points, freezing water at 7.5 degrees, and boiling water at 60.0 degrees. What is the boiling point of oxygen, 90.2 K, on the Rømer scale?
103. What is the percent error of thinking the melting point of tungsten is 3695°C instead of the correct value of 3695 K?
104. An engineer wants to design a structure in which the difference in length between a steel beam and an aluminum beam remains at 0.500 m regardless of temperature, for ordinary temperatures. What must the lengths of the beams be?
105. How much stress is created in a steel beam if its temperature changes from –15°C to 40°C but it cannot expand? For steel, the Young’s modulus \(Y=210×10^9N/m^2\) from Stress, Strain, and Elastic Modulus. (Ignore the change in area resulting from the expansion.)
106. A brass rod (\(Y=90×10^9N/m^2\)), with a diameter of 0.800 cm and a length of 1.20 m when the temperature is 25°C, is fixed at both ends. At what temperature is the force in it at 36,000 N?
107. A mercury thermometer still in use for meteorology has a bulb with a volume of \(0.780cm^3\) and a tube for the mercury to expand into of inside diameter 0.130 mm. (a) Neglecting the thermal expansion of the glass, what is the spacing between marks 1°C apart? (b) If the thermometer is made of ordinary glass (not a good idea), what is the spacing?
108. Even when shut down after a period of normal use, a large commercial nuclear reactor transfers thermal energy at the rate of 150 MW by the radioactive decay of fission products. This heat transfer causes a rapid increase in temperature if the cooling system fails (1watt=1joule/second or 1W=1J/s and 1MW=1megawatt).
(a) Calculate the rate of temperature increase in degrees Celsius per second (°C/s) if the mass of the reactor core is \(1.60×10^5kg\)and it has an average specific heat of 0.3349kJ/kg⋅°C.
(b) How long would it take to obtain a temperature increase of 2000°C, which could cause some metals holding the radioactive materials to melt? (The initial rate of temperature increase would be greater than that calculated here because the heat transfer is concentrated in a smaller mass. Later, however, the temperature increase would slow down because the 500,000-kg steel containment vessel would also begin to heat up.)
109. You leave a pastry in the refrigerator on a plate and ask your roommate to take it out before you get home so you can eat it at room temperature, the way you like it. Instead, your roommate plays video games for hours. When you return, you notice that the pastry is still cold, but the game console has become hot. Annoyed, and knowing that the pastry will not be good if it is microwaved, you warm up the pastry by unplugging the console and putting it in a clean trash bag (which acts as a perfect calorimeter) with the pastry on the plate. After a while, you find that the equilibrium temperature is a nice, warm 38.3°C. You know that the game console has a mass of 2.1 kg. Approximate it as having a uniform initial temperature of 45°C. The pastry has a mass of 0.16 kg and a specific heat of 3.0kJ/(kg⋅ºC), and is at a uniform initial temperature of 4.0°C. The plate is at the same temperature and has a mass of 0.24 kg and a specific heat of 0.90J/(kg⋅ºC). What is the specific heat of the console?
110. Two solid spheres, A and B, made of the same material, are at temperatures of 0°C and 100°C, respectively. The spheres are placed in thermal contact in an ideal calorimeter, and they reach an equilibrium temperature of 20°C. Which is the bigger sphere? What is the ratio of their diameters?
111. In some countries, liquid nitrogen is used on dairy trucks instead of mechanical refrigerators. A 3.00-hour delivery trip requires 200 L of liquid nitrogen, which has a density of \(808kg/m^3.\).
(a) Calculate the heat transfer necessary to evaporate this amount of liquid nitrogen and raise its temperature to 3.00°C. (Use \(c_P\) and assume it is constant over the temperature range.) This value is the amount of cooling the liquid nitrogen supplies.
(b) What is this heat transfer rate in kilowatt-hours?
(c) Compare the amount of cooling obtained from melting an identical mass of 0-°C ice with that from evaporating the liquid nitrogen.
112. Some gun fanciers make their own bullets, which involves melting lead and casting it into lead slugs. How much heat transfer is needed to raise the temperature and melt 0.500 kg of lead, starting from 25.0°C?
113. A 0.800-kg iron cylinder at a temperature of \(1.00×10^3°C\) is dropped into an insulated chest of 1.00 kg of ice at its melting point. What is the final temperature, and how much ice has melted?
114. Repeat the preceding problem with 2.00 kg of ice instead of 1.00 kg.
115. Repeat the preceding problem with 0.500 kg of ice, assuming that the ice is initially in a copper container of mass 1.50 kg in equilibrium with the ice.
116. A 30.0-g ice cube at its melting point is dropped into an aluminum calorimeter of mass 100.0 g in equilibrium at 24.0°C with 300.0 g of an unknown liquid. The final temperature is 4.0°C. What is the heat capacity of the liquid?
117. (a) Calculate the rate of heat conduction through a double-paned window that has a \(1.50-m^2\) area and is made of two panes of 0.800-cm-thick glass separated by a 1.00-cm air gap. The inside surface temperature is 15.0°C,15.0°C, while that on the outside is −10.0°C.(Hint: There are identical temperature drops across the two glass panes. First find these and then the temperature drop across the air gap. This problem ignores the increased heat transfer in the air gap due to convection.)
(b) Calculate the rate of heat conduction through a 1.60-cm-thick window of the same area and with the same temperatures. Compare your answer with that for part (a).
118. (a) An exterior wall of a house is 3 m tall and 10 m wide. It consists of a layer of drywall with an R factor of 0.56, a layer 3.5 inches thick filled with fiberglass batts, and a layer of insulated siding with an R factor of 2.6. The wall is built so well that there are no leaks of air through it. When the inside of the wall is at 22°C and the outside is at −2°C, what is the rate of heat flow through the wall?
(b) More realistically, the 3.5-inch space also contains 2-by-4 studs—wooden boards 1.5 inches by 3.5 inches oriented so that 3.5-inch dimension extends from the drywall to the siding. They are “on 16-inch centers,” that is, the centers of the studs are 16 inches apart. What is the heat current in this situation? Don’t worry about one stud more or less.
119. For the human body, what is the rate of heat transfer by conduction through the body’s tissue with the following conditions: the tissue thickness is 3.00 cm, the difference in temperature is 2.00°C, and the skin area is1.50m21.50m2. How does this compare with the average heat transfer rate to the body resulting from an energy intake of about 2400 kcal per day? (No exercise is included.)
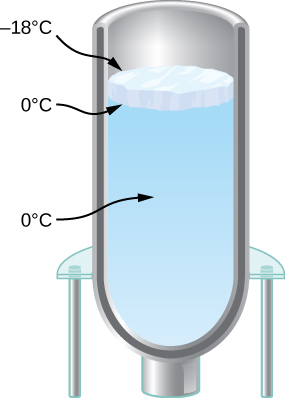
120. You have a Dewar flask (a laboratory vacuum flask) that has an open top and straight sides, as shown below. You fill it with water and put it into the freezer. It is effectively a perfect insulator, blocking all heat transfer, except on the top. After a time, ice forms on the surface of the water. The liquid water and the bottom surface of the ice, in contact with the liquid water, are at 0°C. The top surface of the ice is at the same temperature as the air in the freezer, −18°C. Set the rate of heat flow through the ice equal to the rate of loss of heat of fusion as the water freezes. When the ice layer is 0.700 cm thick, find the rate in m/s at which the ice is thickening.
121. An infrared heater for a sauna has a surface area of \(0.050m^2\) and an emissivity of 0.84. What temperature must it run at if the required power is 360 W? Neglect the temperature of the environment.
122. (a) Determine the power of radiation from the Sun by noting that the intensity of the radiation at the distance of Earth is \(1370W/m^2\. Hint: That intensity will be found everywhere on a spherical surface with radius equal to that of Earth’s orbit.
(b) Assuming that the Sun’s temperature is 5780 K and that its emissivity is 1, find its radius.
Challenge Problems
123. A pendulum is made of a rod of length L and negligible mass, but capable of thermal expansion, and a weight of negligible size.
(a) Show that when the temperature increases by dT, the period of the pendulum increases by a fraction αLdT/2.
(b) A clock controlled by a brass pendulum keeps time correctly at 10°C. If the room temperature is 30°C, does the clock run faster or slower? What is its error in seconds per day?
124. At temperatures of a few hundred kelvins the specific heat capacity of copper approximately follows the empirical formula \(c=α+βT+δT^{−2}\), where α=349J/kg⋅K, \(β=0.107J/kg⋅K^2\), and \(δ=4.58×10^5J⋅kg⋅K\). How much heat is needed to raise the temperature of a 2.00-kg piece of copper from 20°C to 250°C?
125. In a calorimeter of negligible heat capacity, 200 g of steam at 150°C and 100 g of ice at −40°C are mixed. The pressure is maintained at 1 atm. What is the final temperature, and how much steam, ice, and water are present?
126. An astronaut performing an extra-vehicular activity (space walk) shaded from the Sun is wearing a spacesuit that can be approximated as perfectly white (e=0) except for a 5cm×8cm patch in the form of the astronaut’s national flag. The patch has emissivity 0.300. The spacesuit under the patch is 0.500 cm thick, with a thermal conductivity k=0.0600W/m°C, and its inner surface is at a temperature of 20.0°C. What is the temperature of the patch, and what is the rate of heat loss through it? Assume the patch is so thin that its outer surface is at the same temperature as the outer surface of the spacesuit under it. Also assume the temperature of outer space is 0 K. You will get an equation that is very hard to solve in closed form, so you can solve it numerically with a graphing calculator, with software, or even by trial and error with a calculator.
127. The goal in this problem is to find the growth of an ice layer as a function of time. Call the thickness of the ice layer L.
(a) Derive an equation for dL/dt in terms of L , the temperature T above the ice, and the properties of ice (which you can leave in symbolic form instead of substituting the numbers).
(b) Solve this differential equation assuming that at t=0, you have L=0. If you have studied differential equations, you will know a technique for solving equations of this type: manipulate the equation to get dL/dt multiplied by a (very simple) function of L on one side, and integrate both sides with respect to time. Alternatively, you may be able to use your knowledge of the derivatives of various functions to guess the solution, which has a simple dependence on t.
(c) Will the water eventually freeze to the bottom of the flask?
128. As the very first rudiment of climatology, estimate the temperature of Earth. Assume it is a perfect sphere and its temperature is uniform. Ignore the greenhouse effect. Thermal radiation from the Sun has an intensity (the “solar constant” S) of about \(1370W/m^2\) at the radius of Earth’s orbit.
(a) Assuming the Sun’s rays are parallel, what area must S be multiplied by to get the total radiation intercepted by Earth? It will be easiest to answer in terms of Earth’s radius, R.
(b) Assume that Earth reflects about 30% of the solar energy it intercepts. In other words, Earth has an albedo with a value of A=0.3. In terms of S, A, and R, what is the rate at which Earth absorbs energy from the Sun?
(c) Find the temperature at which Earth radiates energy at the same rate. Assume that at the infrared wavelengths where it radiates, the emissivity e is 1. Does your result show that the greenhouse effect is important?
(d) How does your answer depend on the the area of Earth?
129. Let’s stop ignoring the greenhouse effect and incorporate it into the previous problem in a very rough way. Assume the atmosphere is a single layer, a spherical shell around Earth, with an emissivity e=0.77 (chosen simply to give the right answer) at infrared wavelengths emitted by Earth and by the atmosphere. However, the atmosphere is transparent to the Sun’s radiation (that is, assume the radiation is at visible wavelengths with no infrared), so the Sun’s radiation reaches the surface. The greenhouse effect comes from the difference between the atmosphere’s transmission of visible light and its rather strong absorption of infrared. Note that the atmosphere’s radius is not significantly different from Earth’s, but since the atmosphere is a layer above Earth, it emits radiation both upward and downward, so it has twice Earth’s area. There are three radiative energy transfers in this problem: solar radiation absorbed by Earth’s surface; infrared radiation from the surface, which is absorbed by the atmosphere according to its emissivity; and infrared radiation from the atmosphere, half of which is absorbed by Earth and half of which goes out into space. Apply the method of the previous problem to get an equation for Earth’s surface and one for the atmosphere, and solve them for the two unknown temperatures, surface and atmosphere.
a. In terms of Earth’s radius, the constant σσ, and the unknown temperature \(T_s\) of the surface, what is the power of the infrared radiation from the surface?
b. What is the power of Earth’s radiation absorbed by the atmosphere?
c. In terms of the unknown temperature \(T_e\) of the atmosphere, what is the power radiated from the atmosphere?
d. Write an equation that says the power of the radiation the atmosphere absorbs from Earth equals the power of the radiation it emits.
e. Half of the power radiated by the atmosphere hits Earth. Write an equation that says that the power Earth absorbs from the atmosphere and the Sun equals the power that it emits.
f. Solve your two equations for the unknown temperature of Earth.
For steps that make this model less crude, see for example the lectures by Paul O’Gorman.
Contributors and Attributions
Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University), and Bill Moebs with many contributing authors. This work is licensed by OpenStax University Physics under a Creative Commons Attribution License (by 4.0).