13.7: The Third Law of Thermodynamics
- Last updated
- Jun 17, 2019
- Save as PDF
- Page ID
- 18085

- Boundless
- Boundless
( \newcommand{\kernel}{\mathrm{null}\,}\)
learning objectives
- Explain how absolute zero affects entropy
The third law of thermodynamics is sometimes stated as follows: The entropy of a perfect crystal at absolute zero is exactly equal to zero.
At zero kelvin the system must be in a state with the minimum possible energy, thus this statement of the third law holds true if the perfect crystal has only one minimum energy state. Entropy is related to the number of possible microstates, and with only one microstate available at zero kelvin the entropy is exactly zero.
The third law was developed by the chemist Walther Nernst during the years 1906-1912. It is often referred to as Nernst’s theorem or Nernst’s postulate. Nernst proposed that the entropy of a system at absolute zero would be a well-defined constant. Instead of being 0, entropy at absolute zero could be a nonzero constant, due to the fact that a system may have degeneracy (having several ground states at the same energy).
In simple terms, the third law states that the entropy of a perfect crystal approaches zero as the absolute temperature approaches zero. This law provides an absolute reference point for the determination of entropy. ( diagrams the temperature entropy of nitrogen. ) The entropy (S) determined relative to this point is the absolute entropy represented as follows:
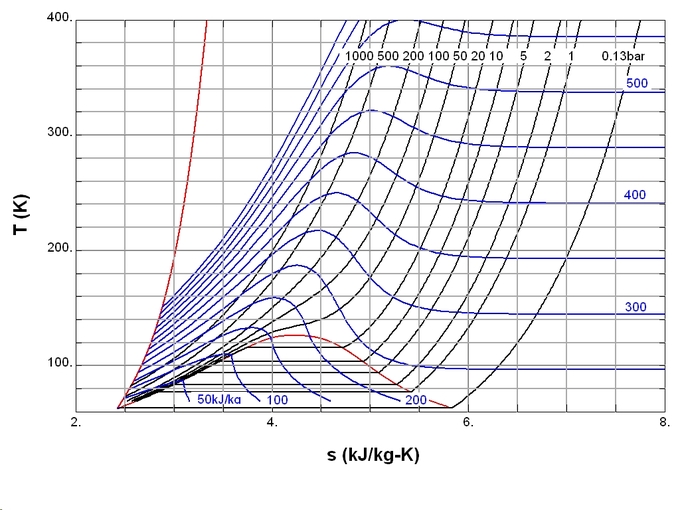
Temperature Entropy of Nitrogen: Temperature–entropy diagram of nitrogen. The red curve at the left is the melting curve. Absolute value of entropy can be determined shown here, thanks to the third law of thermodynamics.
S=kBlogW,
where kB is the Bolzmann constant and W is the number of microstates. Provided that the ground state is unique (or W=1), the entropy of a perfect crystal lattice as defined by Nernst’s theorem is zero provided that its ground state is unique, because log(1)=0.
Adiabatic Processes
It is impossible to reduce the temperature of any system to zero temperature in a finite number of finite operations.
learning objectives
- Illustrate isentropic process, for example in terms of adiabtic demangetization
In our Atom on “Adiabatic Processes” (category: the First Law of Thermodynamics), we learned that an adiabatic process is any process occurring without gain or loss of heat within a system. We also learned a monatomic ideal gas expands adiabatically. In this Atom, we discuss an adiabatic cooling process that can be used to cool a gas, as well as whether absolute zero can be obtained in real systems.
Absolute Zero?
Previously, we learned about the third law of thermodynamics, which states: the entropy of a perfect crystal at absolute zero is exactly equal to zero.
According to the third law, the reason that T=0 cannot be reached is explained as follows: Suppose the temperature of a substance can be reduced in an isentropic process by changing the parameter X from X2 to X1. As an example, one can think of a multistage adiabatic magnetization-demagnetization cycle setup where a magnetic field is switched on and off in a controlled way. (See below. The parameter X in this case would be the magnetization of the gas. )
Assuming an entropy difference at absolute zero, T=0 could be reached in a finite number of steps. However, going back to the third law, at T=0 there is no entropy difference, and therefore an infinite number of stepswould be needed for this process (illustrated in ).
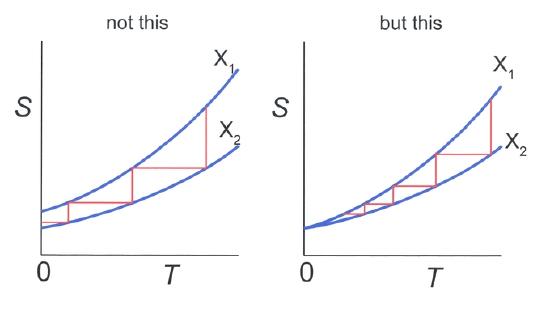
Can Absolute Zero be Reached?: Temperature-Entropy diagram. Horizontal lines represent isentropic processes, while vertical lines represent isothermal processes. Left side: Absolute zero can be reached in a finite number of steps if S(T=0,X1)≠S(T=0, X2). Right: An infinite number of steps is needed since S(0,X1)= S(0,X2).
Adiabatic Demagnetization Cooling
In simple terms, the cooling scheme mentioned above occurs by repeating the following steps:
- A strong magnetic field is applied to adiabatically align magnetic moments of the particles in the gas.
- The magnetic field is reduced adiabatically, and thermal energy of the gas causes “ordered” magnetic moments to become random again.
In the second step, thermal energy in the gas is used to cause disorder of magnetic moments. Therefore, the temperature of the gas is reduced (hence cooling works). This scheme is called adiabatic demagnetization cooling.
Key Points
- Entropy is related to the number of possible microstates, and with only one microstate available at zero kelvin, the entropy is exactly zero.
- The third law of thermodynamics provides an absolute reference point for the determination of entropy. The entropy determined relative to this point is the absolute entropy.
- Absolute entropy can be written as S=kB\logW, where W is the number of available microstates.
- Since at T=0 there is no entropy difference, an infinite number of steps in a thermodynamic cooling process is required to reach T=0.
- In adiabatic demagnetization cooling, energy transfers from thermal entropy to magnetic entropy (or disorder of the magnetic moments).
- The fact that T=0 cannot be achieved in reality is a direct consequence of the third law of thermodynamics.
Key Terms
- microstate: The specific detailed microscopic configuration of a system.
- absolute zero: The coldest possible temperature: zero on the Kelvin scale and approximately -273.15°C and -459.67°F. The total absence of heat; the temperature at which motion of all molecules would cease.
- degeneracy: Two or more different quantum states are said to be degenerate if they are all at the same energy level.
- isentropic: Having a constant entropy.
- demagnetization: The process of removing the magnetic field from an object.
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
- Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- absolute zero. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/absolute_zero. License: CC BY-SA: Attribution-ShareAlike
- Third law of thermodynamics. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Third_l...thermodynamics. License: CC BY-SA: Attribution-ShareAlike
- degeneracy. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/degeneracy. License: CC BY-SA: Attribution-ShareAlike
- microstate. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/microstate. License: CC BY-SA: Attribution-ShareAlike
- Entropy (classical thermodynamics). Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Entropy...hermodynamics). License: CC BY: Attribution
- absolute zero. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/absolute_zero. License: CC BY-SA: Attribution-ShareAlike
- Magnetic refrigeration. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Magnetic_refrigeration. License: CC BY-SA: Attribution-ShareAlike
- Third law of thermodynamics. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Third_l...thermodynamics. License: CC BY-SA: Attribution-ShareAlike
- demagnetization. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/demagnetization. License: CC BY-SA: Attribution-ShareAlike
- isentropic. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/isentropic. License: CC BY-SA: Attribution-ShareAlike
- Entropy (classical thermodynamics). Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Entropy...hermodynamics). License: CC BY: Attribution
- Third law of thermodynamics. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Third_l...thermodynamics. License: Public Domain: No Known Copyright

