6.3: Newton’s Laws
- Last updated
- Save as PDF
- Page ID
- 18150

- Boundless
- Boundless
The First Law: Inertia
Newton’s first law of motion describes inertia. According to this law, a body at rest tends to stay at rest, and a body in motion tends to stay in motion, unless acted on by a net external force.
learning objectives
- Define the First Law of Motion
History
Sir Isaac Newton was an English scientist who was interested in the motion of objects under various conditions. In 1687, he published a work called Philosophiae Naturalis Principla Mathematica, which described his three laws of motion. Newton used these laws to explain and explore the motion of physical objects and systems. These laws form the basis for mechanics. The laws describe the relationship between forces acting on a body and the motions experienced due to these forces. The three laws are as follows:
- If an object experiences no net force, its velocity will remain constant. The object is either at rest and the velocity is zero or it moves in a straight line with a constant speed.
- The acceleration of an object is parallel and directly proportional to the net force acting on the object, is in the direction of the net force, and is inversely proportional to the mass of the object.
- When a first object exerts a force on a second object, the second object simultaneously exerts a force on the first object, meaning that the force of the first object and the force of the second object are equal in magnitude and opposite in direction.
The First Law of Motion
You have most likely heard Newton’s first law of motion before. If you haven’t heard it in the form written above, you have probably heard that “a body in motion stays in motion, and a body at rest stays at rest.” This means that an object that is in motion will not change its velocity unless an unbalanced force acts upon it. This is called uniform motion. It is easier to explain this concept through examples.
Example \(\PageIndex{1}\):
If you are ice skating, and you push yourself away from the side of the rink, according to Newton’s first law you will continue all the way to the other side of the rink. But, this won’t actually happen. Newton says that a body in motion will stay in motion until an outside force acts upon it. In this and most other real world cases, this outside force is friction. The friction between your ice skates and the ice is what causes you to slow down and eventually stop.
Let’s look at another situation. Refer to for this example. Why do we wear seat belts? Obviously, they’re there to protect us from injury in case of a car accident. If a car is traveling at 60 mph, the driver is also traveling at 60 mph. When the car suddenly stops, an external force is applied to the car that causes it to slow down. But there is no force acting on the driver, so the driver continues to travel at 60 mph. The seat belt is there to counteract this and act as that external force to slow the driver down along with the car, preventing them from being harmed.
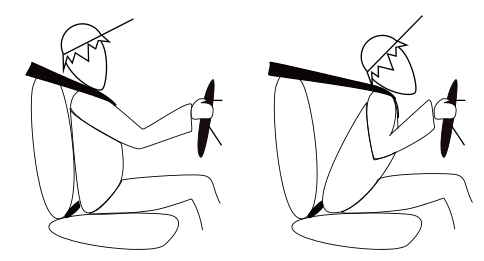
Newton’s First Law: Newton’s first law in effect on the driver of a car
Inertia
Sometimes this first law of motion is referred to as the law of inertia. Inertia is the property of a body to remain at rest or to remain in motion with constant velocity. Some objects have more inertia than others because the inertia of an object is equivalent to its mass. This is why it is more difficult to change the direction of a boulder than a baseball.
Doc Physics – Newton: Newton’s first law is hugely counterintuitive. You may have learned it in gradeschool, though. Let’s see it for the mind-blowing conclusion it really is.
The Second Law: Force and Acceleration
The second law states that the net force on an object is equal to the rate of change, or derivative, of its linear momentum.
learning objectives
- Define the Second Law of Motion
English scientist Sir Isaac Newton examined the motion of physical objects and systems under various conditions. In 1687, he published his three laws of motion in Philosophiae Naturalis Principla Mathematica. The laws form the basis for mechanics—they describe the relationship between forces acting on a body, and the motion experienced due to these forces. These three laws state:
- If an object experiences no net force, its velocity will remain constant. The object is either at rest and the velocity is zero, or it moves in a straight line with a constant speed.
- The acceleration of an object is parallel and directly proportional to the net force acting on the object, is in the direction of the net force and is inversely proportional to the mass of the object.
- When a first object exerts a force on a second object, the second object simultaneously exerts a force on the first object, meaning that the force of the first object and the force of the second object are equal in magnitude and opposite in direction.
The first law of motion defines only the natural state of the motion of the body (i.e., when the net force is zero). It does not allow us to quantify the force and acceleration of a body. The acceleration is the rate of change in velocity; it is caused only by an external force acting on it. The second law of motion states that the net force on an object is equal to the rate of change of its linear momentum.
Linear Momentum
Linear momentum of an object is a vector quantity that has both magnitude and direction. It is the product of mass and velocity of a particle at a given time:
\[\mathrm{p=mv}\]
where, \(\mathrm{p=momentum, m=mass,}\) and \(\mathrm{v=velocity}\). From this equation, we see that objects with more mass will have more momentum.
The Second Law of Motion
Picture two balls of different mass, traveling in the same direction at the same velocity. If they both collide with a wall at the same time, the heavier ball will exert a larger force on the wall. This concept, illustrated below, explains Newton’s second law, which emphasizes the importance of force and motion, over velocity alone. It states: the net force on an object is equal to the rate of change of its linear momentum. From calculus we know that the rate of change is the same as a derivative. When we the linear momentum of an object we get:

Force and Mass: This animation demonstrates the connection between force and mass.
\[\begin{align} \mathrm{F \; } & \mathrm{=\dfrac{dp}{dt}} \\ \mathrm{F \;} & \mathrm{=\dfrac{d(m⋅v)}{dt}} \end{align}\]
where, \(\mathrm{F = Force}\) and \(\mathrm{t = time}\). From this we can further simplify the equation:
\[\begin{align} \mathrm{F \;} & \mathrm{=m\dfrac{d(v)}{dt}} \\ \mathrm{F \;} & \mathrm{=m⋅a} \end{align}\]
where, a=accelerationa=acceleration. As we stated earlier, acceleration is the rate of change of velocity, or velocity divided by time.
Newton’s Three Laws of Mechanics – Second Law – Part 1: Here we’ll see how many people can confuse your understanding of Newton’s 2nd law of motion through oversight, sloppy language, or cruel intentions.
Newton’s Three Laws of Mechanics – Second Law – Part Two: Equilibrium is investigated and Newton’s 1st law is seen as a special case of Newton’s 2nd law!
The Third Law: Symmetry in Forces
The third law of motion states that for every action, there is an equal and opposite reaction.
learning objectives
- Define the Third Law of Motion
Sir Isaac Newton was a scientist from England who was interested in the motion of objects under various conditions. In 1687, he published a work called Philosophiae Naturalis Principla Mathematica, which contained his three laws of motion. Newton used these laws to explain and explore the motion of physical objects and systems. These laws form the bases for mechanics. The laws describe the relationship between forces acting on a body, and the motion is an experience due to these forces. Newton’s three laws are:
- If an object experiences no net force, its velocity will remain constant. The object is either at rest and the velocity is zero or it moves in a straight line with a constant speed.
- The acceleration of an object is parallel and directly proportional to the net force acting on the object, is in the direction of the net force and is inversely proportional to the mass of the object.
- When a first object exerts a force on a second object, the second object simultaneously exerts a force on the first object, meaning that the force of the first object and the force of the second object are equal in magnitude and opposite in direction.
Newton’s Third Law of Motion
Newton’s third law basically states that for every action, there is an equal and opposite reaction. If object A exerts a force on object B, because of the law of symmetry, object B will exert a force on object A that is equal to the force acted on it:
\[\mathrm{FA=−FB}\]
In this example, FA is the action and FB is the reaction. You have undoubtedly witnessed this law of motion. For example, take a swimmer who uses her feet to push off the wall in order to gain speed. The more force she exerts on the wall, the harder she pushes off. This is because the wall exerts the same force on her that she forces on it. She pushes the wall in the direction behind her, therefore the wall will exert a force on her that is in the direction in front of her and propel her forward.
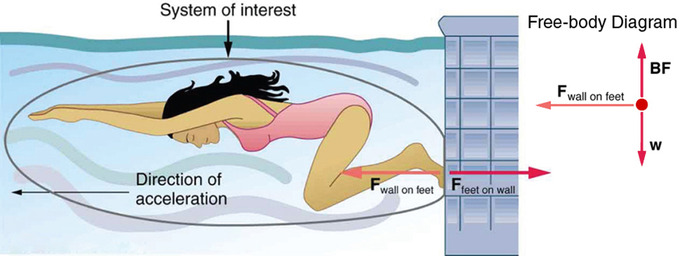
Newton’s Third Law of Motion: When a swimmer pushes off the wall, the swimmer is using the third law of motion.
Take as another example, the concept of thrust. When a rocket launches into outer space, it expels gas backward at a high velocity. The rocket exerts a large backward force on the gas, and the gas exerts and equal and opposite reaction force forward on the rocket, causing it to launch. This force is called thrust. Thrust is used in cars and planes as well.
Newton’s Third Law: The most fundamental statement of basic physical reality is also the most often misunderstood. As your mom if she’s clear on Newton’s Third. Then ask her why things can move if every force has a paired opposite force all the time, forever.
Key Points
- Newton’s three laws of physics are the basis for mechanics.
- The first law states that a body at rest will stay at rest until a net external force acts upon it and that a body in motion will remain in motion at a constant velocity until acted on by a net external force.
- Net external force is the sum of all of the forcing acting on an object.
- Just because there are forces acting on an object doesn’t necessarily mean that there is a net external force; forces that are equal in magnitude but acting in opposite directions can cancel one another out.
- Friction is the force between an object in motion and the surface on which it moves. Friction is the external force that acts on objects and causes them to slow down when no other external force acts upon them.
- Inertia is the tendency of a body in motion to remain in motion. Inertia is dependent on mass, which is why it is harder to change the direction of a heavy body in motion than it is to change the direction of a lighter object in motion.
- Newton’s three laws of motion explain the relationship between forces acting on an object and the motion they experience due to these forces. These laws act as the basis for mechanics.
- The second law explains the relationship between force and motion, as opposed to velocity and motion. It uses the concept of linear momentum to do this.
- Linear momentum \(\mathrm{p}\), is the product of mass \(\mathrm{m}\), and velocity \(\mathrm{v: p=mv}\).
- The second law states that the net force is equal to the derivative, or rate of change of its linear momentum.
- By simplifying this relationship and remembering that acceleration is the rate of change of velocity, we can see that the second law of motion is where the relationship between force and acceleration comes from.
- If an object A exerts a force on object B, object B exerts an equal and opposite force on object A.
- Newton’s third law can be seen in many everyday circumstances. When you walk, the force you use to push off the ground backwards makes you move forward.
- Thrust is an application of the third law of motion. A helicopter uses thrust to push the air under the propeller down, and therefore lift off the ground.
Key Terms
- inertia: The property of a body that resists any change to its uniform motion; equivalent to its mass.
- friction: A force that resists the relative motion or tendency to such motion of two bodies in contact.
- uniform motion: Motion at a constant velocity (with zero acceleration). Note that an object in motion will not change its velocity unless an unbalanced force acts upon it.
- net force: The combination of all the forces that act on an object.
- momentum: (of a body in motion) the product of its mass and velocity.
- acceleration: The amount by which a speed or velocity increases (and so a scalar quantity or a vector quantity).
- symmetry: Exact correspondence on either side of a dividing line, plane, center or axis.
- thrust: The force generated by propulsion, as in a jet engine.
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
- Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- OpenStax College, Newtonu2019s First Law of Motion: Inertia. September 18, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42130/latest/. License: CC BY: Attribution
- Newtons first law. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Newtons_first_law. License: CC BY-SA: Attribution-ShareAlike
- Free High School Science Texts Project, Forces: Newton's First Law. September 18, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m38960/latest/. License: CC BY: Attribution
- friction. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/friction. License: CC BY-SA: Attribution-ShareAlike
- inertia. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/inertia. License: CC BY-SA: Attribution-ShareAlike
- uniform motion. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/uniform%20motion. License: CC BY-SA: Attribution-ShareAlike
- Doc Physics - Newton. Located at: http://www.youtube.com/watch?v=cliJbHYpNic. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Free High School Science Texts Project, Forces: Newton's First Law. January 18, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m38960/latest/. License: CC BY: Attribution
- net force. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/net_force. License: CC BY-SA: Attribution-ShareAlike
- Sunil Kumar Singh, Newton's Second Law of Motion. September 18, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m14042/latest/. License: CC BY: Attribution
- Newtons first law. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Newtons_first_law. License: CC BY-SA: Attribution-ShareAlike
- momentum. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/momentum. License: CC BY-SA: Attribution-ShareAlike
- acceleration. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/acceleration. License: CC BY-SA: Attribution-ShareAlike
- Doc Physics - Newton. Located at: http://www.youtube.com/watch?v=cliJbHYpNic. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Free High School Science Texts Project, Forces: Newton's First Law. January 18, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m38960/latest/. License: CC BY: Attribution
- Newton's Three Laws of Mechanics - Second Law - Part 1. Located at: http://www.youtube.com/watch?v=dFybXASirwQ. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Elastischer stou00df3. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Elastischer_sto%C3%9F3.gif. License: CC BY-SA: Attribution-ShareAlike
- Newton's Three Laws of Mechanics - Second Law - Part Two. Located at: http://www.youtube.com/watch?v=_Z7qivqbSBI. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- OpenStax College, Newtonu2019s Third Law of Motion: Symmetry in Forces. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42074/latest/. License: CC BY: Attribution
- Newtons first law. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Newtons_first_law. License: CC BY-SA: Attribution-ShareAlike
- symmetry. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/symmetry. License: CC BY-SA: Attribution-ShareAlike
- thrust. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/thrust. License: CC BY-SA: Attribution-ShareAlike
- Doc Physics - Newton. Located at: http://www.youtube.com/watch?v=cliJbHYpNic. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Free High School Science Texts Project, Forces: Newton's First Law. January 18, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m38960/latest/. License: CC BY: Attribution
- Newton's Three Laws of Mechanics - Second Law - Part 1. Located at: http://www.youtube.com/watch?v=dFybXASirwQ. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Elastischer stou00df3. Provided by: Wikipedia. Located at: http://en.Wikipedia.org/wiki/File:Elastischer_sto%C3%9F3.gif. License: CC BY-SA: Attribution-ShareAlike
- Newton's Three Laws of Mechanics - Second Law - Part Two. Located at: http://www.youtube.com/watch?v=_Z7qivqbSBI. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- OpenStax College, Newtonu2019s Third Law of Motion: Symmetry in Forces. January 25, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42074/latest/. License: CC BY: Attribution
- Newton's Third Law. Located at: http://www.youtube.com/watch?v=VR7NfNWuPLk. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license

